lqg
線形 2 次ガウシアン (LQG) 設計
構文
reg = lqg(sys,QXU,QWV)
reg = lqg(sys,QXU,QWV,QI)
reg = lqg(sys,QXU,QWV,QI,'1dof')
reg = lqg(sys,QXU,QWV,QI,'2dof')
reg = lqg(___,'current')
[reg,info] = lqg(___)
説明
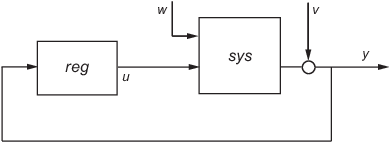
reg = lqg(sys,QXU,QWV) は、プラントの状態空間モデル sys と重み行列 QXU とQWV を与えて最適な線形 2 次ガウシアン (LQG) レギュレーター reg を計算します。ダイナミック レギュレーター reg は、0 の値の周りで y を調節する制御信号 u を生成するために、測定値 y を使用します。このレギュレーターをプラント出力 y に接続するには、正のフィードバックを使用してください。
LQG レギュレーターは、次のコスト関数を最小化します。
これは、以下のプラント方程式の下で行われます。
ここで、プロセス ノイズw、観測ノイズ v は、以下の共分散をもつガウス性ホワイト ノイズです。
reg = lqg(sys,QXU,QWV,QI) は、制御信号 u を生成するために、設定値コマンド r と測定値 y を使用します。reg は、y がこのコマンド r をトラッキングするような積分動作を行います。

LQG サーボコントローラーは、次のコスト関数を最小化します。
ここで、xi は追従誤差 r - y の積分です。MIMO システムの場合、r、y、xi は、同じ長さでなければなりません。
reg = lqg(sys,QXU,QWV,QI,'1dof') は、入力として [r ; y] ではなく e = r - y をもつ自由度 1 のサーボ コントローラーを計算します。
reg = lqg(sys,QXU,QWV,QI,'2dof') は、LQG(sys,QXU,QWV,QI) と等価であり、前述した自由度 2 のサーボコントローラーを生成します。
reg = lqg(___,'current') は、"現在の" カルマン推定器を使用します。この推定器は離散時間システムの LQG レギュレーターを計算する際、状態推定値として x[n|n] を使用します。
[reg,info] = lqg(___) は、前述の任意の構文で、コントローラーと推定器のゲイン行列を構造体 info に返します。コントローラーと推定器のゲインは、たとえばコントローラーをオブザーバー形式で実装する場合などに使用できます。詳細については、アルゴリズムを参照してください。
例
線形 2 次ガウシアン (LQG) レギュレーターとサーボ コントローラーの設計
この例では、線形 2 次ガウシアン (LQG) レギュレーター、自由度 1 の LQG サーボ コントローラー、および自由度 2 の LQG サーボ コントローラーを次のシステム用に設計する方法を示します。

プラントには、3 つの状態 (x)、2 つの制御入力 (u)、3 つのランダム入力 (w)、1 つの出力 (y)、出力の測定ノイズ (v)、および次の状態方程式と測定方程式があります。
ここで、
システムには次のノイズ共分散データがあります。
レギュレーターでは、次のコスト関数を使用してレギュレーション性能と制御操作とのトレードオフを定義します。
サーボ コントローラーでは、次のコスト関数を使用してトラッカーの性能と制御操作とのトレードオフを定義します。
このシステムの LQG コントローラーを設計するには
MATLAB コマンド ウィンドウに次のように入力して、状態空間システムを作成します。
A = [0 1 0;0 0 1;1 0 0]; B = [0.3 1;0 1;-0.3 0.9]; C = [1.9 1.3 1]; D = [0.53 -0.61]; sys = ss(A,B,C,D);
次のコマンドを入力して、ノイズ共分散データと重み行列を定義します。
nx = 3; %Number of states ny = 1; %Number of outputs Qn = [4 2 0; 2 1 0; 0 0 1]; Rn = 0.7; R = [1 0;0 2] QXU = blkdiag(0.1*eye(nx),R); QWV = blkdiag(Qn,Rn); QI = eye(ny);
次のコマンドを入力して、LQG レギュレーターを作成します。
このコマンドは、次の LQG レギュレーターを返します。KLQG = lqg(sys,QXU,QWV)
A = x1_e x2_e x3_e x1_e -6.212 -3.814 -4.136 x2_e -4.038 -3.196 -1.791 x3_e -1.418 -1.973 -1.766 B = y1 x1_e 2.365 x2_e 1.432 x3_e 0.7684 C = x1_e x2_e x3_e u1 -0.02904 0.0008272 0.0303 u2 -0.7147 -0.7115 -0.7132 D = y1 u1 0 u2 0 Input groups: Name Channels Measurement 1 Output groups: Name Channels Controls 1,2 Continuous-time model.次のコマンドを入力して、自由度 1 の LQG サーボ コントローラーを作成します。
このコマンドは、次の LQG サーボ コントローラーを返します。KLQG1 = lqg(sys,QXU,QWV,QI,'1dof')A = x1_e x2_e x3_e xi1 x1_e -7.626 -5.068 -4.891 0.9018 x2_e -5.108 -4.146 -2.362 0.6762 x3_e -2.121 -2.604 -2.141 0.4088 xi1 0 0 0 0 B = e1 x1_e -2.365 x2_e -1.432 x3_e -0.7684 xi1 1 C = x1_e x2_e x3_e xi1 u1 -0.5388 -0.4173 -0.2481 0.5578 u2 -1.492 -1.388 -1.131 0.5869 D = e1 u1 0 u2 0 Input groups: Name Channels Error 1 Output groups: Name Channels Controls 1,2 Continuous-time model.次のコマンドを入力して、自由度 2 の LQG サーボ コントローラーを作成します。
このコマンドは、次の LQG サーボ コントローラーを返します。KLQG2 = lqg(sys,QXU,QWV,QI,'2dof')A = x1_e x2_e x3_e xi1 x1_e -7.626 -5.068 -4.891 0.9018 x2_e -5.108 -4.146 -2.362 0.6762 x3_e -2.121 -2.604 -2.141 0.4088 xi1 0 0 0 0 B = r1 y1 x1_e 0 2.365 x2_e 0 1.432 x3_e 0 0.7684 xi1 1 -1 C = x1_e x2_e x3_e xi1 u1 -0.5388 -0.4173 -0.2481 0.5578 u2 -1.492 -1.388 -1.131 0.5869 D = r1 y1 u1 0 0 u2 0 0 Input groups: Name Channels Setpoint 1 Measurement 2 Output groups: Name Channels Controls 1,2 Continuous-time model.
ヒント
lqgは、連続、離散時間プラントの両方で使用することができます。離散時間の場合、lqgはその状態推定値として既定で x[n|n-1] を使用します。x[n|n] を状態推定値に使用して最適な LQG コントローラーを計算するには、'current'入力引数を使用します。状態推定器の詳細については、kalmanを参照してください。LQG レギュレーターを計算するには、
lqgはコマンドlqrとkalmanを使用します。サーボコントローラーを計算するには、lqgはコマンドlqiとkalmanを使用します。レギュレーターの設計に柔軟性をもたせる場合は、
lqr、kalman、lqgregコマンドを使用できます。サーボ コントローラーの設計に柔軟性をもたせる場合は、lqi、kalman、lqgtrackコマンドを使用できます。これらのコマンドの使用方法および使用状況の判断方法については、レギュレーターの線形 2 次ガウシアン (LQG) 設計と線形 2 次ガウシアン (LQG) 法による積分動作を含むサーボ コントローラーの設計を参照してください。
アルゴリズム
コントローラーの方程式は次のとおりです。
連続時間の場合:
離散時間の場合:
遅延推定器:
現在の推定器:
ここで
A、B、C および D は、LQG レギュレーター
regの状態空間行列です。xi は追従誤差 r - y の積分です。
Kx、Kw、Ki、L、Mx および Mw は、
infoに返されるコントローラーと推定器のゲイン行列です。
バージョン履歴
R2006a より前に導入