lqgtrack
線形 2 次ガウシアン (LQG) サーボ コントローラーの作成
構文
C = lqgtrack(kest,k)
C = lqgtrack(kest,k,'2dof')
C = lqgtrack(kest,k,'1dof')
C = lqgtrack(kest,k,...CONTROLS)
説明
lqgtrack は次の図に示すループに対して積分動作をもつ線形 2 次ガウシアン (LQG) サーボ コントローラーを作成します。この補償器は、出力 y が設定値 r を追従し、プロセス外乱 w と観測ノイズ v を除外するようにします。lqgtrack は、r と y が同じ長さであるものと仮定します。

メモ
LQG サーボ コントローラー C をプラント出力 y に接続する際には、必ず正のフィードバックを使用してください。
C = lqgtrack(kest,k) は次の図に示すように、カルマン推定器 kest と状態フィードバック ゲイン k を接続することで、自由度 2 の LQG サーボ コントローラー C を作成します。C は入力 をもち、コマンド を生成します。ここで、 はプラント状態のカルマン推定であり、xi は積分器の出力です。
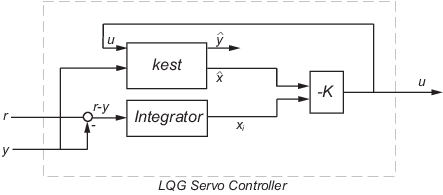
ゲイン行列 k のサイズは、xi の長さを決定します。xi、y、および r は、同じ長さをもっています。
自由度 2 の LQG サーボ コントローラーの状態空間方程式は次のようになります。
メモ
構文 C = lqgtrack(kest,k,'2dof') は、C = lqgtrack(kest,k) と等価です。
C = lqgtrack(kest,k,'1dof') は次の図に示すように、[r ; y] の代わりの入力として、トラッキング エラー e = r – y を取る自由度 1 の LQG サーボ コントローラー C を生成します。

自由度 1 の LQG サーボ コントローラーの状態空間方程式は次のようになります。
C = lqgtrack(kest,k,...CONTROLS) はカルマン推定器 kest がプラントの追加の既知の (確定的) コマンド Ud にアクセスしたときに LQG サーボ コントローラー C を作成します。インデックス ベクトル CONTROLS は、kest のどの入力が制御チャネル u であるかを指定します。結果の補償器 C は、次の入力をもちます。
[Ud ; r ; y] (自由度 2 の場合)
[Ud ; e] (自由度 1 の場合)
対応する補償器は、自由度 2 の場合に以下に示す構造で表示されます。

例
LQG サーボ コントローラーの設計の例を参照してください。
ヒント
連続時間、および離散時間システムの両方で lqgtrack を使用できます。
離散時間の場合、積分器は、前進オイラー法に基づきます (詳細は lqi を参照)。状態推定 は、推定器のタイプによって x[n|n] または x[n|n–1] になります (詳細については kalman を参照)。
方程式をもつ離散時間プラントの場合:
"現在の" カルマン推定器を LQR ゲインに連結するのが最適であるのは、 であり、かつ y[n] が w[n] に依存しない (H = 0) 場合のみです。これらの条件が満たされない場合、lqg を使用して最適な LQG コントローラーを計算してください。
バージョン履歴
R2008b で導入