lqgreg

線形 2 次ガウシアン (LQG) レギュレーターの作成

構文

rlqg = lqgreg(kest,k) rlqg = lqgreg(kest,k,controls)

説明

rlqg = lqgreg(kest,k) は、カルマン推定器を kest、状態フィードバックゲイン行列を k として、LQG レギュレーター rlqg (状態空間モデル) を返します。同じ関数で、連続時間と離散時間の両方の場合が処理されます。kest と k の設計には同じツールを使用してください。

連続プラントの連続レギュレーター: lqr または lqry および kalman を使用
離散プラントの離散レギュレーター: dlqr または lqry および kalman を使用
連続プラントの離散レギュレーター: lqrd と kalmd を使用

離散時間の場合、lqgreg が

レギュレーター $u [n] = - K \hat{x} [n | n]$ を生成するのは、kest が "現在の" カルマン推定器の場合
レギュレーター $u [n] = - K \hat{x} [n | n - 1]$ を生成するのは、kest が "遅延" カルマン推定器の場合

カルマン推定器の詳細は、kalman のリファレンスページを参照してください。

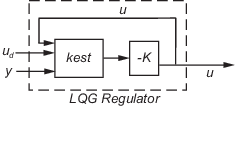
rlqg = lqgreg(kest,k,controls) は、追加の既知のプラント入力 u_d にアクセスする推定器を扱います。インデックスベクトル controls は、推定器のどの入力が制御する u かを指定します。また、結果の LQG レギュレーター rlqg は u_d および y を入力にもちます (次の図を参照)。

メモ

LQG レギュレーターをプラントに接続する際には、必ず正のフィードバックを使用してください。

例

LQG レギュレーター: 圧延機のケーススタディの例を参照してください。

アルゴリズム

lqgreg は kalman で設計したカルマン推定器と lqr、dlqr または lqry で設計した最適状態フィードバックゲインを接続することで、線形 2 次ガウシアン (LQG) レギュレーターを作成します。LQG レギュレーターは、レギュレーションの性能と制御のトレードオフを行うある 2 次コスト関数を最小化します。このレギュレーターはダイナミックで、安定化指令を生成するノイズの測定値に依存します。

連続時間では、LQG レギュレーターは次の指令値を生成します。

$u = - K \hat{x}$

ここで、 $\hat{x}$ はカルマン状態推定です。レギュレーターの状態空間方程式は以下のとおりです。

$\begin{array}{l} \dot{\hat{x}} = [A - L C - (B - L D) K] \hat{x} + L y \\ u = - K \hat{x} \end{array}$

ここで y はプラント出力測定量のベクトルです (背景と表記については、kalman を参照)。以下の図は、プラントに対するダイナミックレギュレーターを示しています。

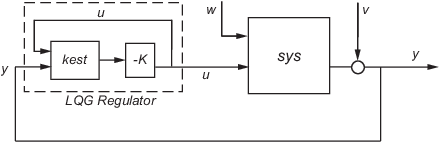
離散時間の場合は、y[n–1] までの測定値に基づいた x[n] の遅延状態推定 $\hat{x} [n | n - 1]$ か、y[n] を含む使用可能なすべての測定値に基づいた現在の状態推定 $\hat{x} [n | n]$ のいずれかを使用して LQG レギュレーターを作成できます。レギュレーター

$u [n] = - K \hat{x} [n | n - 1]$

は常に適切に定義されていますが、"現在のレギュレーター"

$u [n] = - K \hat{x} [n | n]$

は I-KMD が可逆の場合にのみ因果的になります (表記については kalman を参照)。さらに現在のレギュレーターを実際に実装した場合は、測定値 y[n] が使用可能になった後の u[n] の計算するための時間が必要です (これがフィードバックループのむだ時間になります)。

方程式をもつ離散時間プラントの場合:

$\begin{matrix} x [n + 1] = A x [n] + B u [n] + G w [n] \\ y [n] = C x [n] + D u [n] + H w [n] + v [n] {Measurements} \end{matrix}$

"現在の" カルマン推定器を LQR ゲインに連結するのが最適であるのは、 $E (w [n] v {[n]}^{'}) = 0$ であり、かつ y[n] が w[n] に依存しない (H = 0) 場合のみです。これらの条件が満たされない場合、lqg を使用して最適な LQG コントローラーを計算してください。

バージョン履歴

R2006a より前に導入

参考