正しいモデル表現の使用
この例では、LTI モデルで作業する場合のベスト プラクティスを示します。
どの表現が計算に最も適しているか
Control System Toolbox™ ソフトウェアを使用すると、LTI システムを次の 4 通りの方法で表現できます。
伝達関数 (TF)
零点-極-ゲイン (ZPK)
状態空間 (SS)
周波数応答データ (FRD)
TF 表現と ZPK 表現はコンパクトで表示するのに便利ですが、以下の理由のためにシステムの操作や解析には適していません。
TF モデルや ZPK モデルを使用すると、評価の不正確性を伴う高次の多項式が生成されることが多い。
TF 表現と ZPK 表現は、MIMO システムの操作には非効率であり、モデルの次数を引き上げる傾向がある。
これらの制約については以下で説明します。これらの制約のため、LTI モデルに関連した計算には、ほとんどの場合 SS 表現または FRD 表現を使用する必要があります。
高次の伝達関数に伴う落とし穴
高次の伝達関数を伴う計算では、正確性が著しく損なわれるだけでなく、オーバーフローが発生する場合もあります。2 つの伝達関数の単純な積を計算しただけでも、以下に示すような予期しない結果が得られることがあります。
次数がそれぞれ 9 と 2 である、2 つの離散時間伝達関数 Pd および Cd を読み込み、プロットします。
% Load Pd,Cd models load numdemo Pd Cd % Plot their frequency response bode(Pd,'b',Cd,'r'), grid legend('Pd','Cd')

次に、TF、ZPK、SS、および FRD の各表現を使用して、開ループ伝達関数 L = Pd*Cd を計算します。
Ltf = Pd * Cd; % TF Lzp = zpk(Pd) * Cd; % ZPK Lss = ss(Pd) * Cd; % SS w = logspace(-1,3,100); Lfrd = frd(Pd,w) * Cd; % FRD
最後に、結果として生成される 4 つのモデルの周波数応答の振幅を計算します。
sigma(Ltf,'b--',Lzp,'g',Lss,'r:',Lfrd,'m--',{1e-1,1e3}); legend('TF','ZPK','SS','FRD')

ZPK、SS、および FRD の各表現からの応答は厳密に一致しますが、TF 表現からの応答は 100 rad/sec より下において不規則的かつ不均一になります。この伝達関数における精度の低下について理解するには、z=1 における Pd および Cd の極/零点配置図を比較します。
pzplot(Pd,'b',Cd,'r'); title('Pole/zero maps of Pd (blue) and Cd (red)'); axis([0.4 1.05 -1 1])

z=1 近傍には重根があります。多項式の値の相対的な精度は根の近くで低下するため、z=1 近傍における伝達関数値の相対誤差は 100% を上回ります。100 rad/s より下の周波数は |z-1|<1e-3 にマッピングされ、それが 100 rad/s より下では一貫性のない結果となる理由です。
表現間の変換および復元に伴う落とし穴
tf、zpk、および ss の各コマンドを使用すると、任意の LTI モデルをそれぞれ伝達関数、零点-極-ゲイン、または状態空間の形式に容易に変換できます。たとえば、次のように入力して、2 つの入力と 2 つの出力をもつランダム状態空間モデル HSS1 を作成したとします。
HSS1 = rss(3,2,2);
次のように入力すると、このモデルの伝達関数を取得できます。
HTF = tf(HSS1);
また、次のように入力すると、伝達関数を状態空間モデルに戻すことができます。
HSS2 = ss(HTF);
ただし、このような表現間の変換/復元は、計算コストのかかる操作であり、結果の精度を下げるだけでなく、MIMO システムのモデルの次数を人為的に引き上げる可能性もあります。たとえば、次数 3 の分母をもつ 2 行 2 列の伝達行列の一般次数は 6 であるため、HSS2 の次数は HSS1 の次数の 2 倍になります。
order(HSS1)
ans = 3
order(HSS2)
ans = 6
モデルの次数の違いを理解するには、2 つのモデルの極/零点配置図を比較します。
subplot(211) pzmap(HSS1,'b') title('Poles and zeros of HSS1'); subplot(212) pzmap(HSS2,'r') title('Poles and zeros of HSS2');

この極/零点配置図では、HSS2 の極/零点のペアの相殺が o の内側の x によって表されています。コマンド minreal を使用すると、極/零点のペアの相殺を除去して、3 次の最小状態空間モデルを HSS2 から復元できます。
HSS2_min = minreal(HSS2);
3 states removed.
order(HSS2_min)
ans = 3
これら 2 つのモデル間の相対ギャップをプロットすることにより、HSS1 と HSS2_min が一致しているかどうかをチェックします。
clf Gap = HSS1-HSS2_min; sigma(HSS1,Gap), grid legend('HSS1','Gap HSS1 vs. minimal HSS2','Location','Best')
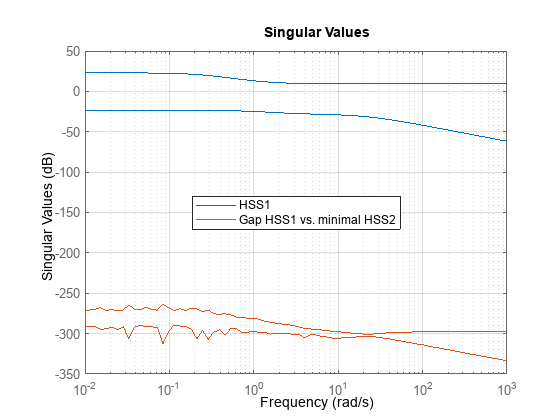
どの周波数でもギャップ (緑色の曲線) は非常に小さくなります。Gap プロットに "ノイズが含まれる" という警告が sigma によって示されますが、これは、差異が小さすぎて基本的に丸め誤差でプロットが構成されているためです。
最小実現を抽出することは数値的に複雑なため、非最小モデルの作成は避けるべきです。システムの相互接続における状態の重複を防ぐの関連情報も参照してください。