システムの相互接続における状態の重複を防ぐ

この例では、LTI システム相互接続の最小次数モデルを構築する際のガイドラインを示します。

モデルの相互接続

+、*、[,]、[;] の各演算子と series、parallel、feedback、lft の各コマンドを使用して、複数の LTI モデルを接続することができます。一部のダイナミクスの重複を防ぎ、結果として生成されるモデルの次数が最小になるようにするには、次の簡単な規則に従うことが重要となります。

接続する前にすべてのモデルを状態空間表現に変換しておく
ブロック線図の構造に従う
閉形式表現と伝達関数の代数の使用を避ける

説明のため、この例では、次のブロック線図の状態空間モデルを計算するための 2 つの方法を比較します。

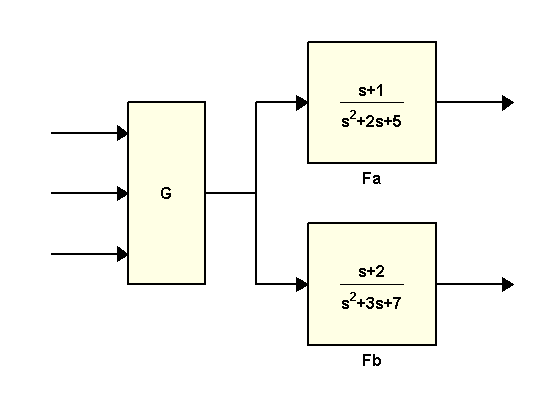
ここで

G = [1 , tf(1,[1 0]) , 5];
Fa = tf([1 1] , [1 2 5]);
Fb = tf([1 2] , [1 3 7]);

推奨される方法

これら 3 つのブロックを接続するための最良の方法は、ブロックを状態空間に変換して、そのブロック線図を G と [Fa;Fb] の直列接続として扱うことです。

H1 = [ss(Fa) ; Fb] * G;

H1 の次数を求めるには、次のように入力します。

order(H1)

ans = 5

次数 5 は最小の次数です。SS は TF より優先順位が高いため、3 つのブロックのいずれかを状態空間に変換するだけで十分です (残りの変換は自動的に行われます)。

次数引き上げ方法

この伝達関数は全体として次のようになっています。

$H (s) = (\begin{array}{c} F_{a} (s) G (s) \\ F_{b} (s) G (s) \end{array})$

したがって、次を入力することで、3 つのブロックを接続して H を計算することもできます。

H2 = ss([Fa * G ; Fb * G]);

H1 と H2 の周波数応答が一致していることを確認します。

bode(H1,'b',H2,'r--')

H2 は有効なモデルですが、次数が 14 であり、H1 の次数のほぼ 3 倍になります。

order(H2)

ans = 14

H2 の次数の方が高い理由は次のとおりです。

G がこの式に 2 回出現する
Fa*G と Fb*G を評価するときに、Fa と Fb のダイナミクスが 3 回複製される
次数 2 の要素を 4 つと次数 3 の要素を 2 つもつ 2x3 の MIMO 伝達行列に対して状態空間の変換が実行され、合計 14 の次数が生成される

伝達関数全体として閉じた形の式を使用することは、次数を引き上げ、多数の極/零点ダイナミクスの相殺を生じさせる原因となるため、一般的に推奨されません。

まとめ

LTI モデルを接続する際は、閉じた形の式の使用を避け、状態空間表現を使用し、基本的な直列結合、並列結合、およびフィードバック結合にブロック線図を分割することによって、ダイナミクスの重複が生じるのを防ぎます。確信がもてない場合は、関数 connect を使用してください。すべてのモデルを自動的に状態空間に変換し、ブロック線図の最小実現を生成することが保証されています。