フィードバック ループを閉じるために FEEDBACK を使用

フィードバック ループを閉じるための 2 とおりの方法

次のようなフィードバック ループがあるとします。

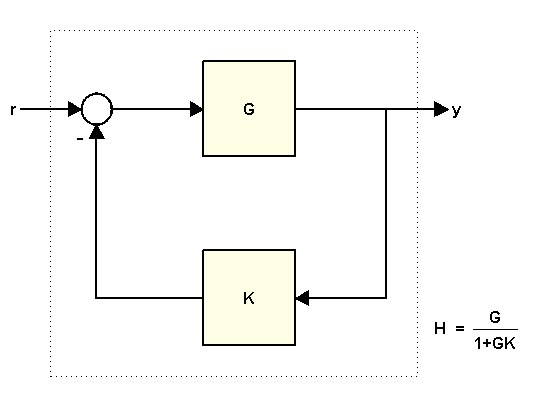
ここで、

K = 2;
G = tf([1 2],[1 .5 3])

G =
 
       s + 2
  ---------------
  s^2 + 0.5 s + 3
 
Continuous-time transfer function.
Model Properties

r から y への閉ループ伝達関数 H は、少なくとも次の 2 とおりの方法で計算できます。

feedback を使用して H を計算するには、次のように入力します。

H = feedback(G,K)

H =
 
       s + 2
  ---------------
  s^2 + 2.5 s + 7
 
Continuous-time transfer function.
Model Properties

式から H を計算するには、次のように入力します。

H2 = G/(1+G*K)

H2 =
 
        s^3 + 2.5 s^2 + 4 s + 6
  -----------------------------------
  s^4 + 3 s^3 + 11.25 s^2 + 11 s + 21
 
Continuous-time transfer function.
Model Properties

FEEDBACK を使用することがなぜ好ましいか

式から H を計算する際に大きな問題となるのは、閉ループ伝達関数の次数が上がることです。上記の例では、H2 の次数が H の 2 倍になっています。これは、式 G/(1+G*K) が、G と 1+G*K という 2 つの伝達関数の比率として評価されるためです。ここで、

である場合、G/(1+G*K) は次のように評価されます。

その結果、G の極が H の分子と分母の両方に追加されます。このことは、次の ZPK 表現を見ることで確認できます。

zpk(H2)

ans =
 
       (s+2) (s^2 + 0.5s + 3)
  ---------------------------------
  (s^2 + 0.5s + 3) (s^2 + 2.5s + 7)
 
Continuous-time zero/pole/gain model.
Model Properties

このように極と零点が余分に追加されると、次の例で示すように、高次の伝達関数を処理する際に結果の精度が下がる可能性があります。この例には、17 次の伝達関数 G が関与しています。先ほどと同じように、2 とおりの方法を使って、K=1 とした場合の閉ループ伝達関数を計算します。

load numdemo G
H1 = feedback(G,1);          % good
H2 = G/(1+G);                % bad

基準点を設定するため、G の周波数応答が含まれた FRD モデルも計算し、周波数応答データに feedback を直接適用します。

w = logspace(2,5.1,100);
H0 = feedback(frd(G,w),1);

次に、閉ループ応答の振幅を比較します。

sigmaplot(H0,'b',H1,'g--',H2,'r');
legend('Reference H0','H1=feedback(G,1)','H2=G/(1+G)','location','southwest');
ylim([-60 0])

H2 の周波数応答は、2e4 rad/sec より低い周波数では不正確になります。この不正確性の原因としては、z=1 近傍で追加 (相殺) 的なダイナミクスが導入されていることが考えられます。具体的に言うと、H2 には、z=1 の近傍に H1 の約 2 倍の極と零点があります。その結果、H2(z) の z=1 近傍では精度が大幅に低くなり、低周波数での応答に歪みが生じます。詳細については、正しいモデル表現の使用の例を参照してください。