pid2

並列形式の 2-DOF PID コントローラー

説明

pid2 は、並列形式の 2 自由度 (2-DOF) の比例-積分-微分 (PID) コントローラー モデル オブジェクトを作成したり、動的システム モデルを並列 2-DOF PID コントローラー形式に変換したりする場合に使用します。

2-DOF PID コントローラーには、比例項および微分項に設定点の重みが含まれています。2-DOF PID コントローラーでは、外乱の抑制を、設定点の追従におけるオーバーシュートを大きく増加させることなく迅速に実行できます。2-DOF PID コントローラーはまた、制御信号に対する基準信号の変化の影響を緩和するためにも有用です。次の図では、2-DOF PID コントローラーを使用した典型的な制御アーキテクチャが示されています。

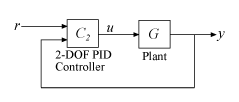
pid2 コントローラー モデル オブジェクトは、並列形式 PID コントローラーを連続時間または離散時間で表現できます。

• 連続時間 — $$u=K_p\left(br-y\right)+\frac{K_i}{s}\left(r-y\right)+\frac{K_{d}s}{T_{f}s+1}\left(cr-y\right)$$

• 離散時間 — $$u=K_p\left(br-y\right)+K_{i}IF\left(z\right)\left(r-y\right)+\frac{K_d}{T_f+DF\left(z\right)}\left(cr-y\right)$$

ここで

• b は比例項での設定点の重みです。

• c は微分項での設定点の重みです。

• K_p は比例ゲインです。

• K_i は積分ゲインです。

• K_d は微分ゲインです。

• T_f は 1 次微分フィルター時定数です。

• IF(z) は離散時間コントローラーで積分を計算するための積分手法です。

• DF(z) は離散時間コントローラーで微分フィルターを計算するための積分手法です。

このオブジェクトを、制御アーキテクチャのプラント、アクチュエータ、センサーなど、他のコンポーネントと組み合わせて、制御システムを表すことができます。詳細については、モデル オブジェクトでの制御システム モデリングを参照してください。

コントローラーのパラメーターを直接指定するか、別のタイプのモデル (伝達関数モデル tf など) を PID コントローラー形式に変換して、PID コントローラー モデル オブジェクトを作成できます。

pid2 を使用して、一般化状態空間 (genss) モデルや不確かさをもつ状態空間 (uss (Robust Control Toolbox)) モデルを作成することもできます。

作成

pid2 コントローラー モデルは次のいずれかの方法で取得できます。

• 関数 pid2 を使用してモデルを作成する。

• 関数 pidtune を使用して、プラント モデル用に PID コントローラーを調整する。関数 pidtune の引数 type で 2-DOF PID コントローラー タイプを指定して、並列形式 2-DOF PID コントローラーを取得する。以下に例を示します。

  sys = zpk([],[-1 -1 -1],1);
  C2 = pidtune(sys,'PID2');

• 以下を使用して、プラント モデル用に PID コントローラーを対話的に調整する:

  • [PID コントローラーの調整] ライブ エディター タスク。

  • PID 調整器アプリ。

構文

C2 = pid2(Kp,Ki,Kd,Tf,b,c)

C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts)

C2 = pid2(___,Name,Value)

C2 = pid2

C2 = pid2(sys)

説明

C2 = pid2(Kp,Ki,Kd,Tf,b,c) は、連続時間 2-DOF 並列形式 PID コントローラー モデルを作成し、Kp、Ki、Kd、Tf、b、c の各プロパティを設定します。残りのプロパティは既定値をもちます。

C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts) は、サンプル時間 Ts をもつ離散時間 2-DOF PID コントローラー モデルを作成します。

C2 = pid2(___,Name,Value) は、前述の入力引数の任意の組み合わせについて引数 Name,Value を 1 つ以上使用して指定される、pid2 コントローラー オブジェクトのプロパティを設定します。

C2 = pid2 は、既定のプロパティ値をもつコントローラー オブジェクトを作成します。コントローラー モデルのプロパティを変更するには、ドット表記を使用します。

C2 = pid2(sys) は、動的システム モデル sys を並列形式 pid2 コントローラー オブジェクトに変換します。

入力引数

Kp — 比例ゲイン

1 (既定値) | スカラー | ベクトル | 行列 | realp オブジェクト | genmat オブジェクト | tunableSurface オブジェクト

比例ゲイン。有限の実数値または調整可能なオブジェクトとして指定します。

• pid2 コントローラー オブジェクトを作成するには、有限の実数スカラー値を使用します。

• pid2 コントローラー オブジェクトの配列を作成するには、有限の実数値の配列を使用します。

• 調整可能なコントローラー モデルを作成するには、調整可能なパラメーター (realp) または一般化行列 (genmat) を使用します。

• 調整可能なゲインスケジュール コントローラー モデルを作成するには、tunableSurface を使用して作成された調整可能な曲面を使用します。

Ki — 積分ゲイン

0 (既定値) | スカラー | ベクトル | 行列 | realp オブジェクト | genmat オブジェクト | tunableSurface オブジェクト

積分ゲイン。有限の実数値または調整可能なオブジェクトとして指定します。

• pid2 コントローラー オブジェクトを作成するには、有限の実数スカラー値を使用します。

• pid2 コントローラー オブジェクトの配列を作成するには、有限の実数値の配列を使用します。

• 調整可能なコントローラー モデルを作成するには、調整可能なパラメーター (realp) または一般化行列 (genmat) を使用します。

• 調整可能なゲインスケジュール コントローラー モデルを作成するには、tunableSurface を使用して作成された調整可能な曲面を使用します。

Kd — 微分ゲイン

0 (既定値) | スカラー | ベクトル | 行列 | realp オブジェクト | genmat オブジェクト | tunableSurface オブジェクト

微分ゲイン。有限の実数値または調整可能なオブジェクトとして指定します。

• pid2 コントローラー オブジェクトを作成するには、有限の実数スカラー値を使用します。

• pid2 コントローラー オブジェクトの配列を作成するには、有限の実数値の配列を使用します。

• 調整可能なコントローラー モデルを作成するには、調整可能なパラメーター (realp) または一般化行列 (genmat) を使用します。

• 調整可能なゲインスケジュール コントローラー モデルを作成するには、tunableSurface を使用して作成された調整可能な曲面を使用します。

Tf — 微分フィルター時定数

0 (既定値) | スカラー | ベクトル | 行列 | realp オブジェクト | genmat オブジェクト | tunableSurface オブジェクト

1 次微分フィルターの時定数。有限の実数値または調整可能なオブジェクトとして指定します。

• pid2 コントローラー オブジェクトを作成するには、有限の実数スカラー値を使用します。

• pid2 コントローラー オブジェクトの配列を作成するには、有限の実数値の配列を使用します。

• 調整可能なコントローラー モデルを作成するには、調整可能なパラメーター (realp) または一般化行列 (genmat) を使用します。

• 調整可能なゲインスケジュール コントローラー モデルを作成するには、tunableSurface を使用して作成された調整可能な曲面を使用します。

b — 比例項での設定点の重み付け

1 (既定値) | スカラー | ベクトル | 行列 | realp オブジェクト | genmat オブジェクト | tunableSurface オブジェクト

比例項での設定点の重み付け。有限の実数値または調整可能なオブジェクトとして指定します。

• pid2 コントローラー オブジェクトを作成するには、有限の実数スカラー値を使用します。

• pid2 コントローラー オブジェクトの配列を作成するには、有限の実数値の配列を使用します。

• 調整可能なコントローラー モデルを作成するには、調整可能なパラメーター (realp) または一般化行列 (genmat) を使用します。

• 調整可能なゲインスケジュール コントローラー モデルを作成するには、tunableSurface を使用して作成された調整可能な曲面を使用します。

b = 0 の場合、設定点での変更が比例項に直接及ぶことはありません。

c — 微分項での設定点の重み付け

1 (既定値) | スカラー | ベクトル | 行列 | realp オブジェクト | genmat オブジェクト | tunableSurface オブジェクト

微分項での設定点の重み付け。有限の実数値または調整可能なオブジェクトとして指定します。

• pid2 コントローラー オブジェクトを作成するには、有限の実数スカラー値を使用します。

• pid2 コントローラー オブジェクトの配列を作成するには、有限の実数値の配列を使用します。

• 調整可能なコントローラー モデルを作成するには、調整可能なパラメーター (realp) または一般化行列 (genmat) を使用します。

• 調整可能なゲインスケジュール コントローラー モデルを作成するには、tunableSurface を使用して作成された調整可能な曲面を使用します。

c = 0 の場合、設定点での変更が微分項に直接及ぶことはありません。

Ts — サンプル時間

0 (既定値) | 正のスカラー

サンプル時間。以下として指定します。

• 0 (連続時間システムの場合)。

• 離散時間システムのサンプリング周期を表す正のスカラー。Ts は TimeUnit プロパティによって指定される時間単位で指定します。

pid2 コントローラーの配列では、すべてのコントローラーに同じ Ts が適用されます。

PID コントローラー モデルは未指定のサンプル時間 (Ts = -1) をサポートしません。

メモ

Ts を変更してもモデルの離散化やリサンプリングは行われません。連続時間表現と離散時間表現の間の変換を行うには、c2d と d2c を使用します。離散時間システムのサンプル時間を変更するには、d2d を使用します。

離散化されたコントローラーの離散積分器の式は、次の表に示すように、使用する c2d 離散化手法に依存します。

c2d 離散化手法	IFormula	DFormula
'zoh'	ForwardEuler	ForwardEuler
'foh'	Trapezoidal	Trapezoidal
'tustin'	Trapezoidal	Trapezoidal
'impulse'	ForwardEuler	ForwardEuler
'matched'	ForwardEuler	ForwardEuler

c2d 離散化手法の詳細については、c2d を参照してください。

他の離散積分器の式が必要な場合は、Ts、IFormula、および DFormula を目標値に直接設定してコントローラーを離散化することができます。ただし、この方法では離散化されたコントローラーの新しいゲインとフィルター定数値は計算されません。したがって、この方法で得られる連続時間 PID コントローラーと離散時間 PID コントローラー間の一致は、c2d を使用する場合より劣っている可能性があります。

sys — 動的システム

動的システム モデル | モデル配列

動的システム。SISO 動的システム モデル、または SISO 動的システム モデルの配列として指定します。使用できる動的システムには次のようなものがあります。

• tf、zpk、ss、pidstd モデルなど、連続時間または離散時間の数値 LTI モデル。

• genss や uss (Robust Control Toolbox) モデルなどの一般化された、あるいは不確かさをもつ LTI モデル。

  結果の PID コントローラーでは以下が想定されます。

  • 調整可能な制御設計ブロックについては調整可能なコンポーネントの現在値。

  • 不確かさをもつ制御設計ブロックについてはモデルのノミナル値。

• idtf (System Identification Toolbox)、idss (System Identification Toolbox)、idproc (System Identification Toolbox)、idpoly (System Identification Toolbox)、idgrey (System Identification Toolbox) モデルなどの、同定された LTI モデル。

出力引数

C2 — 2-DOF 並列形式 PID コントローラー モデル

pid2 モデル オブジェクト | genss モデル オブジェクト

PID コントローラー モデル。以下として返されます。

• すべてのゲインが数値をもつ場合、2-DOF 並列形式 PID コントローラー (pid2) モデル オブジェクトです。

• 1 つ以上の係数が数値配列である場合、C2 は pid2 コントローラー オブジェクトの配列です。コントローラー タイプ (PI、PID、PDF など) はゲインの値に依存します。たとえば、Td = 0 で、Kp と Ti が非ゼロかつ有限の場合、C2 は PI コントローラーです。

• 1 つ以上の係数が調整可能なパラメーター (realp)、一般化行列 (genmat) または調整可能なゲイン曲面 (tunableSurface) である場合、C2 は一般化状態空間モデル (genss) です。

プロパティ

Kp, Ki, Kd, Tf, b, c — PID コントローラーの係数

スカラー

PID コントローラーの係数。スカラーとして指定します。pid2 コントローラー オブジェクトまたはオブジェクトの配列を作成するときは、これらの係数を入力引数 Kp、Ki、Kd、Tf、b、および c で指定します。

IFormula — 離散時間コントローラーで積分を計算する手法

'ForwardEuler' | 'BackwardEuler' | 'Trapezoidal'

離散時間 pid2 コントローラーの積分器に使用する離散積分器の式 IF(z):

$$u=K_p\left(br-y\right)+K_{i}IF\left(z\right)\left(r-y\right)+\frac{K_d}{T_f+DF\left(z\right)}\left(cr-y\right)$$

IFormula を以下のいずれかとして指定します。

• 'ForwardEuler' — IF(z) = $$\frac{T_s}{z-1}.$$

  この方程式は、コントローラーの帯域幅と比較してナイキスト制限が大きくなるような、小さいサンプル時間に最適です。大きいサンプル時間で ForwardEuler 式を使用すると、連続時間で安定しているシステムを離散化する場合でも不安定となることがあります。

• 'BackwardEuler' — IF(z) = $$\frac{T_{s}z}{z-1}.$$

  BackwardEuler 式の利点は、この式を使用して安定した連続時間システムを離散化すると、常に安定した離散時間結果が得られることです。

• 'Trapezoidal' — IF(z) = $$\frac{T_s}{2}\frac{z+1}{z-1}.$$

  Trapezoidal 式の利点は、この式を使用して安定した連続時間システムを離散化すると、常に安定した離散時間結果が得られることです。使用可能なすべての積分式の中で、離散システムと対応する連続時間システムの周波数領域プロパティが最も近くなるのは Trapezoidal 式です。

C2 が連続時間コントローラーの場合、IFormula は '' です。

DFormula — 離散時間コントローラーで微分を計算する手法

'ForwardEuler' (既定値) | 'BackwardEuler' | 'Trapezoidal'

離散時間 pid2 コントローラーの微分フィルターに使用する離散積分器の式 DF(z):

$$u=K_p\left(br-y\right)+K_{i}IF\left(z\right)\left(r-y\right)+\frac{K_d}{T_f+DF\left(z\right)}\left(cr-y\right)$$

DFormula を以下のいずれかとして指定します。

• 'ForwardEuler' — DF(z) = $$\frac{T_s}{z-1}.$$

  この方程式は、コントローラーの帯域幅と比較してナイキスト制限が大きくなるような、小さいサンプル時間に最適です。大きいサンプル時間で ForwardEuler 式を使用すると、連続時間で安定しているシステムを離散化する場合でも不安定となることがあります。

• 'BackwardEuler' — DF(z) = $$\frac{T_{s}z}{z-1}.$$

  BackwardEuler 式の利点は、この式を使用して安定した連続時間システムを離散化すると、常に安定した離散時間結果が得られることです。

• 'Trapezoidal' — DF(z) = $$\frac{T_s}{2}\frac{z+1}{z-1}.$$

  Trapezoidal 式の利点は、この式を使用して安定した連続時間システムを離散化すると、常に安定した離散時間結果が得られることです。使用可能なすべての積分式の中で、離散システムと対応する連続時間システムの周波数領域プロパティが最も近くなるのは Trapezoidal 式です。

DFormula の Trapezoidal 値は、微分フィルターのない pid2 コントローラー (Tf = 0) には利用できません。

C2 が連続時間コントローラーの場合、DFormula は '' です。

InputDelay — 入力遅延

0 (既定値)

この プロパティ は読み取り専用です。

システム入力のむだ時間。InputDelay は pid2 コントローラー オブジェクトに対しては常に 0 です。

OutputDelay — 出力遅延

0 (既定値)

この プロパティ は読み取り専用です。

システム出力のむだ時間。OutputDelay は pid2 コントローラー オブジェクトに対しては常に 0 です。

Ts — サンプル時間

0 (既定値) | 正のスカラー

サンプル時間。以下として指定します。

• 0 (連続時間システムの場合)。

• 離散時間システムのサンプリング周期を表す正のスカラー。Ts は TimeUnit プロパティで指定された時間単位で指定します。

pid2 が PID コントローラーの配列である場合、すべてのコントローラーに同じ Ts が適用されます。

TimeUnit — 時間変数の単位

'seconds' (既定値) | 'nanoseconds' | 'microseconds' | 'milliseconds' | 'minutes' | 'hours' | 'days' | 'weeks' | 'months' | 'years' | ...

時間変数の単位。次のいずれかとして指定します。

• 'nanoseconds'

• 'microseconds'

• 'milliseconds'

• 'seconds'

• 'minutes'

• 'hours'

• 'days'

• 'weeks'

• 'months'

• 'years'

TimeUnit の変更は他のプロパティには影響しませんが、システム全体の動作が変わります。chgTimeUnit を使用して、システム動作を変更せずに時間単位を変換します。

InputName — 入力チャネル名

文字ベクトル | 文字ベクトルの cell 配列

入力チャネル名。文字ベクトルまたは文字ベクトルの 2 行 1 列の cell 配列として指定します。このプロパティを使用してコントローラー モデルの入力チャネルに名前を付けます。たとえば、次のようにして、名前 setpoint と measurement を 2-DOF PID コントローラー モデル C の入力に割り当てます。

C.InputName = {'setpoint';'measurement'};

または、自動的なベクトル拡張を使用して両方の入力名を割り当てます。以下に例を示します。

C.InputName = 'C-input';

入力名は自動的に {'C-input(1)';'C-input(2)'} へと拡張されます。

省略形表記 u を使用して、InputName プロパティを参照できます。たとえば、C.u は C.InputName と同じです。

以下を含めて、入力チャネル名はいくつかの用途をもちます。

• モデル表示とプロット上のチャネルの識別

• モデル相互接続時における接続点の指定

InputUnit — 入力チャネル単位

文字ベクトルの cell 配列

入力チャネル単位。2 行 1 列の文字ベクトルの cell 配列として指定します。このプロパティを使用して入力信号単位を追跡します。たとえば、次のようにして、単位 Volts を基準入力に割り当て、濃度単位 mol/m^3 を 2-DOF PID コントローラー モデル C の測定入力に割り当てます。

C.InputUnit = {'Volts';'mol/m^3'};

InputUnit はシステムの動作に影響しません。

InputGroup — 入力チャネル グループ

構造体

入力チャネル グループ。このプロパティは PID コントローラー モデルには必要ありません。

既定では、InputGroup はフィールドのない構造体です。

OutputName — 出力チャネル名

'' (既定値) | 文字ベクトル

出力チャネル名。次のいずれかとして指定します。

• 文字ベクトル。

• '' (名前を指定しない)。

たとえば、次のようにして、コントローラー モデル C の出力に名前 'control' を割り当てます。

C.OutputName = 'control';

省略形表記 y を使用して OutputName プロパティを参照することもできます。たとえば、C.y は C.OutputName と同じです。

OutputName の使用目的は次のとおりです。

• モデル表示とプロット上のチャネルの識別

• モデル相互接続時における接続点の指定

OutputUnit — 出力チャネル単位

'' (既定値) | 文字ベクトル

出力チャネル単位。次のいずれかとして指定されます。

• 文字ベクトル。

• '' (単位を指定しない)。

OutputUnit を使用して出力信号の単位を指定します。OutputUnit はシステムの動作に影響しません。

たとえば、次のようにして、コントローラー モデル C の出力に単位 'volts' を割り当てます。

C.OutputUnit = 'volts';

OutputGroup — 出力チャネル グループ

構造体

出力チャネル グループ。このプロパティは PID コントローラー モデルには必要ありません。

既定では、OutputGroup はフィールドのない構造体です。

Notes — ユーザー指定のテキスト

{} (既定値) | 文字ベクトル | 文字ベクトルの cell 配列

システムに関連付けるユーザー指定のテキスト。文字ベクトルまたは文字ベクトルの cell 配列として指定します。たとえば、'System is MIMO' とします。

UserData — ユーザー指定のデータ

[] (既定値) | 任意の MATLAB^® データ型

システムに関連付けるユーザー指定のデータ。任意の MATLAB データ型として指定します。

Name — システム名

'' (既定値) | 文字ベクトル

システム名。文字ベクトルとして指定します。たとえば、'system_1' とします。

SamplingGrid — モデル配列のサンプリング グリッド

構造体配列

モデル配列のサンプリング グリッド。構造体配列として指定します。

SamplingGrid を使用して、モデル配列の各モデルに関連付けられている変数値を追跡します。これには同定された線形時不変 (IDLTI) モデル配列も含まれます。

構造体のフィールド名をサンプリング変数の名前に設定します。フィールドの値を、配列内の各モデルに関連付けられているサンプリングされた変数の値に設定します。すべてのサンプリング変数は数値スカラーでなければならず、サンプル値のすべての配列はモデル配列の次元と一致しなければなりません。

たとえば、t = 0:10 の各時点で線形時変システムのスナップショットを記録することにより、線形モデルの 11 行 1 列の配列 sysarr を作成することができます。次のコードは線形モデルでの時間サンプルを格納します。

 sysarr.SamplingGrid = struct('time',0:10)

同様に、2 つの変数 zeta と w を個別にサンプリングすることにより、6 行 9 列のモデル配列 M を作成できます。次のコードは (zeta,w) の値を M にマッピングします。

[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>)
M.SamplingGrid = struct('zeta',zeta,'w',w)

M を表示する際、配列の各エントリは対応する zeta と w の値を取り込みます。

M

M(:,:,1,1) [zeta=0.3, w=5] =
 
        25
  --------------
  s^2 + 3 s + 25
 

M(:,:,2,1) [zeta=0.35, w=5] =
 
         25
  ----------------
  s^2 + 3.5 s + 25
 
...

複数のパラメーター値または操作点で Simulink^® モデルを線形化することにより生成されたモデル配列の場合、SamplingGrid には配列の各エントリに対応する変数値が自動的に入力されます。たとえば、Simulink Control Design™ のコマンド linearize (Simulink Control Design) および slLinearizer (Simulink Control Design) により、SamplingGrid が自動的に入力されます。

既定では、SamplingGrid はフィールドのない構造体です。

オブジェクト関数

以下のリストには、pid2 モデルで使用できる関数の代表的なサブセットが含まれています。一般に、動的システム モデルに適用できる関数はすべて、pid2 オブジェクトに適用できます。

線形解析

step	動的システムのステップ応答
impulse	動的システムのインパルス応答プロット、インパルス応答データ
lsim	動的システムの任意の入力へのシミュレーションされた時間応答をプロットする。シミュレーションされた応答データ
bode	周波数応答、または振幅と位相データのボード線図
nyquist	周波数応答のナイキスト線図
nichols	周波数応答のニコルス線図
bandwidth	周波数応答帯域幅

安定性解析

pole	動的システムの極
zero	SISO 動的システムの零点とゲイン
pzplot	追加のプロットのカスタマイズ オプションを使用した動的システム モデルの極-零点プロット
margin	ゲイン余裕、位相余裕、および交差周波数

モデルの変換

zpk	零点-極-ゲイン モデル
ss	状態空間モデル
c2d	連続時間から離散時間へモデルを変換
d2c	離散時間から連続時間へモデルを変換
d2d	離散時間モデルのリサンプリング

モデルの相互接続

feedback	複数のモデルのフィードバック接続
connect	動的システムのブロック線図相互接続
series	2 つのモデルの直列接続
parallel	2 つのモデルの並列接続

コントローラー設計

pidtune	線形プラント モデルのための PID 調整アルゴリズム
rlocus	動的システムの根軌跡プロット
piddata	並列形式 PID コントローラーのアクセス係数
make2DOF	1-DOF PID コントローラーの 2-DOF コントローラーへの変換
pidTuner	PID 調整のための PID 調整器を開く
tunablePID	調整可能な PID コントローラー

例

2-DOF PDF コントローラー

比例ゲインと積分ゲイン、および微分項に対するフィルターをもつ連続時間 2-DOF コントローラーを作成します。これを行うには、積分ゲインを 0 に設定します。他のゲインとフィルター時定数を望ましい値に設定します。

Kp = 1;
Ki = 0;   % No integrator
Kd = 3;
Tf = 0.1;
b = 0.5;    % setpoint weight on proportional term
c = 0.5;    % setpoint weight on derivative term
C2 = pid2(Kp,Ki,Kd,Tf,b,c)

C2 =
 
                         s    
  u = Kp (b*r-y) + Kd -------- (c*r-y)
                       Tf*s+1 

  with Kp = 1, Kd = 3, Tf = 0.1, b = 0.5, c = 0.5
 
Continuous-time 2-DOF PDF controller in parallel form.

表示では、コントローラー タイプ、式およびパラメーター値が示され、コントローラーに積分項のないことが確認されます。

離散時間 2-DOF PI コントローラー

台形則による離散化式を使用し、離散時間 2-DOF PI コントローラーを作成します。式は Name,Value 構文を使用して指定します。

Kp = 5;
Ki = 2.4;
Kd = 0;    
Tf = 0; 
b = 0.5;   
c = 0;      
Ts = 0.1;
C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts,'IFormula','Trapezoidal')

C2 =
 
                      Ts*(z+1)
  u = Kp (b*r-y) + Ki -------- (r-y)
                      2*(z-1) 

  with Kp = 5, Ki = 2.4, b = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PI controller in parallel form.

Kd = 0 と設定すると、微分項のない PI コントローラーが指定されます。表示からわかるように、Tf と c の値はこのコントローラーでは使用されません。表示からは、積分器に台形公式が使用されていることもわかります。

名前の付いた入力と出力をもつ 2-DOF PID コントローラー

2-DOF PID コントローラーを作成し、動的システムのプロパティ InputName および OutputName を設定します。入力と出力に名前を付けることが有用なのは、たとえば、PID コントローラーを他の動的システム モデルと connect コマンドを使用して相互接続する場合などです。

C2 = pid2(1,2,3,0,1,1,'InputName',{'r','y'},'OutputName','u')

C2 =
 
                       1              
  u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
                       s              

  with Kp = 1, Ki = 2, Kd = 3, b = 1, c = 1
 
Continuous-time 2-DOF PID controller in parallel form.

2-DOF PID コントローラーには 2 つの入力と 1 つの出力があります。したがって、'InputName' プロパティは各入力に対して 1 つずつ、2 つの名前を含む配列です。モデル表示では PID コントローラーの入力名と出力名は示されませんが、プロパティ値を調べて確認することはできます。たとえば、コントローラーの入力名を確認します。

C2.InputName

ans = 2x1 cell
    {'r'}
    {'y'}

2-DOF PID コントローラーの配列

配列の行については 1 ～ 2 の範囲の比例ゲインをもち、列については 5 ～ 9 の範囲の積分ゲインをもつ 2-DOF PI コントローラーの 2 行 3 列のグリッドを作成します。

PID コントローラーの配列を作成するには、ゲインを表す配列から開始します。

Kp = [1 1 1;2 2 2];
Ki = [5:2:9;5:2:9];

これらの配列を pid2 コマンドに渡すと、コマンドはコントローラーの配列を返します。

pi_array = pid2(Kp,Ki,0,0,0.5,0,'Ts',0.1,'IFormula','BackwardEuler');
size(pi_array)

2x3 array of 2-DOF PID controller.
Each PID has 1 output and 2 inputs.

いくつかの係数にスカラー値を与えた場合、pid2 はそれらを自動的に拡張し、配列のすべてのエントリに同じ値を代入します。たとえば、この例では、配列のすべてのエントリが PI コントローラーになるよう、Kd = Tf = 0 とされます。また、配列のすべてのエントリで b = 0.5 となっています。

配列のエントリには、配列のインデックスを使用してアクセスします。動的システムの配列では、最初の 2 つの次元はモデルの I/O 次元、残りの次元は配列次元です。したがって、次のコマンドでは配列のエントリ (2,3) が抽出されます。

pi23 = pi_array(:,:,2,3)

pi23 =
 
                       Ts*z 
  u = Kp (b*r-y) + Ki ------ (r-y)
                        z-1 

  with Kp = 2, Ki = 9, b = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PI controller in parallel form.

PID コントローラーの配列は、stack コマンドを使用しても作成できます。

C2 = pid2(1,5,0.1,0,0.5,0.5);         % PID controller
C2f = pid2(1,5,0.1,0.5,0.5,0.5);      % PID controller with filter
pid_array = stack(2,C2,C2f);          % stack along 2nd array dimension

これらのコマンドは、コントローラーの 1 行 2 列の配列を返します。

size(pid_array)

1x2 array of 2-DOF PID controller.
Each PID has 1 output and 2 inputs.

配列内の PID コントローラーはすべて、同じサンプル時間、離散積分器の式、および動的システムのプロパティ (InputName、OutputName など) をもっていなければなりません。

標準形式から並列形式への 2-DOF PID コントローラーの変換

標準形式 pidstd2 コントローラーを並列形式に変換します。

標準 PID 形式では、コントローラーの動作は全体的な比例ゲイン Kp、積分器時定数 Ti と微分時定数 Td、そしてフィルター除数 N によって表現されます。どの 2-DOF 標準形式コントローラーも、pid2 コマンドを使用して並列形式に変換できます。たとえば、次の標準形式コントローラーを考えます。

Kp = 2;
Ti = 3;
Td = 4;
N = 50;
b = 0.1;
c = 0.5;
C2_std = pidstd2(Kp,Ti,Td,N,b,c)

C2_std =
 
                       1      1                      s      
  u = Kp * [(b*r-y) + ---- * --- * (r-y) + Td * ------------ * (c*r-y)]
                       Ti     s                  (Td/N)*s+1 

  with Kp = 2, Ti = 3, Td = 4, N = 50, b = 0.1, c = 0.5
 
Continuous-time 2-DOF PIDF controller in standard form

pid2 を使用してこのコントローラーを並列形式に変換します。

C2_par = pid2(C2_std)

C2_par =
 
                       1                s    
  u = Kp (b*r-y) + Ki --- (r-y) + Kd -------- (c*r-y)
                       s              Tf*s+1 

  with Kp = 2, Ki = 0.667, Kd = 8, Tf = 0.08, b = 0.1, c = 0.5
 
Continuous-time 2-DOF PIDF controller in parallel form.

応答プロットにより、2 つの形式が等価であることが確認されます。

bodeplot(C2_par,'b-',C2_std,'r--')
legend('Parallel','Standard','Location','Southeast')

動的システムの並列形式 2-DOF PID コントローラーへの変換

微分フィルターをもつ 2-DOF PID コントローラーを表す離散時間動的システムを、並列 pid2 形式に変換します。

次の状態空間行列は、サンプル時間が 0.1 秒の離散時間 2-DOF PID コントローラーを表します。

A = [1,0;0,0.99];
B = [0.1,-0.1; -0.005,0.01];
C = [3,0.2];
D = [2.6,-5.2];
Ts = 0.1;
sys = ss(A,B,C,D,Ts);

sys を 2-DOF PID 形式に変換した場合、その結果は、変換でどの離散積分器の式を指定するかに依存します。たとえば、既定の ForwardEuler を積分器と微分の両方で使用したとします。

C2fe = pid2(sys)

C2fe =
 
                        Ts                   1     
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ----------- (c*r-y)
                        z-1             Tf+Ts/(z-1)

  with Kp = 5, Ki = 3, Kd = 2, Tf = 10, b = 0.5, c = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

ここで、Trapezoidal 式を使用して変換を行います。

C2trap = pid2(sys,'IFormula','Trapezoidal','DFormula','Trapezoidal')

C2trap =
 
                      Ts*(z+1)                     1         
  u = Kp (b*r-y) + Ki -------- (r-y) + Kd ------------------- (c*r-y)
                      2*(z-1)             Tf+Ts/2*(z+1)/(z-1)

  with Kp = 4.85, Ki = 3, Kd = 2, Tf = 9.95, b = 0.485, c = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

表示には、結果として得られる係数値と関数形式に相違があることが示されます。

連続時間 2-DOF PID コントローラーの離散化

連続時間 2-DOF PID コントローラーを離散化し、積分フィルターと微分フィルターの式を指定します。

連続時間コントローラーを作成し、c2d コマンドのゼロ次ホールド メソッドを使用してこれを離散化します。

C2con = pid2(10,5,3,0.5,1,1);  % continuous-time 2-DOF PIDF controller
C2dis1 = c2d(C2con,0.1,'zoh')

C2dis1 =
 
                        Ts                   1     
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ----------- (c*r-y)
                        z-1             Tf+Ts/(z-1)

  with Kp = 10, Ki = 5, Kd = 3.31, Tf = 0.552, b = 1, c = 1, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

表示には、離散時間コントローラーの新しい PID 係数についての c2d による計算が示されます。

離散化されたコントローラーの離散化積分器の式は、ヒントで説明されているように、c2d の離散化手法に依存します。zoh メソッドでは、IFormula と DFormula のどちらも ForwardEuler です。

C2dis1.IFormula

ans = 
'ForwardEuler'

C2dis1.DFormula

ans = 
'ForwardEuler'

c2d によって返された式の中から異なるものを複数使用する場合、コントローラーの Ts、IFormula、および DFormula プロパティを望ましい値に直接設定できます。

C2dis2 = C2con;
C2dis2.Ts = 0.1; 
C2dis2.IFormula = 'BackwardEuler';
C2dis2.DFormula = 'BackwardEuler';

ただし、これらのコマンドは、離散化されたコントローラーの新しい PID ゲインは計算しません。これを確認するには、C2dis2 を調べ、その係数を C2con および C2dis1 と比較します。

C2dis2

C2dis2 =
 
                       Ts*z                   1      
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ------------- (c*r-y)
                        z-1             Tf+Ts*z/(z-1)

  with Kp = 10, Ki = 5, Kd = 3, Tf = 0.5, b = 1, c = 1, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

ヒント

• 2-DOF コントローラーを 2 つの SISO 制御コンポーネント (フィードバック コントローラーとフィードフォワード コントローラーなど) に分割するには、getComponents を使用します。

• 以下のようにして、pid2 コントローラー オブジェクトの配列を作成します。

  • 係数 Kp、Ki、Kd、Tf、b および c の 1 つ以上について、配列値を指定する。

  • 動的システム sys の配列を指定し、pid2 コントローラー オブジェクトに変換する。

  • stack を使用して、個々のコントローラーまたはより小さい配列から配列を作成する。

  • プラント モデルの配列を pidtune に渡す。

  pid2 コントローラーの配列では、各コントローラーに同じサンプル時間 Ts と、離散積分器の式 IFormula および DFormula がなければなりません。

• 標準形式コントローラーを作成するか、標準形式コントローラーに変換するには、pidstd2 を使用します。標準形式では、コントローラーの動作は全体的な比例ゲイン K_p、積分時間 T_i と微分時間 T_d、そしてフィルター除数 N によって表現されます。たとえば、連続時間標準形式 2-DOF PID コントローラーの入力と出力間の関係は、次の式で与えられます。

  $$u=K_p\left[\left(br-y\right)+\frac{1}{T_{i}s}\left(r-y\right)+\frac{T_{d}s}{\frac{T_d}{N}s+1}\left(cr-y\right)\right]$$

• 連続時間 pid2 コントローラーを離散化するには、以下の 2 つの方法があります。

  • c2d を使用します。c2d は離散化されたコントローラーのための新しいパラメーター値を計算します。離散化されたコントローラーの離散積分器の式は、次の表に示すように、使用する c2d 離散化手法に依存します。

    c2d 離散化手法	IFormula	DFormula
    'zoh'	ForwardEuler	ForwardEuler
    'foh'	Trapezoidal	Trapezoidal
    'tustin'	Trapezoidal	Trapezoidal
    'impulse'	ForwardEuler	ForwardEuler
    'matched'	ForwardEuler	ForwardEuler

    c2d 離散化手法の詳細については、c2d のリファレンス ページを参照してください。IFormula と DFormula の詳細については、プロパティを参照してください。

  • 他の離散積分器の式が必要な場合は、Ts、IFormula、および DFormula を目標値に直接設定してコントローラーを離散化することができます。(連続時間 2-DOF PID コントローラーの離散化を参照。) ただし、この方法では離散化されたコントローラーの新しいゲインとフィルター定数値は計算されません。したがって、この方法で得られる連続時間と離散時間の pid2 コントローラーの一致は、c2d を使用した場合に比べて劣る可能性があります。

バージョン履歴

R2015b で導入

参考

pidstd2 | pid | piddata2 | getComponents | make1DOF | pidtune | pidTuner | tunablePID2 | genss | realp

トピック

• 2 自由度 PID コントローラー
• 離散時間比例-積分-微分 (PID) コントローラー
• モデル オブジェクトとは