2 自由度 PID コントローラー

2 自由度 (2-DOF) PID コントローラーには、比例項および微分項に設定点の重みが含まれています。2-DOF PID コントローラーでは、外乱の抑制を、設定点の追従におけるオーバーシュートを大きく増加させることなく迅速に実行できます。2-DOF PID コントローラーはまた、制御信号に対する基準信号の変化の影響を緩和するためにも有用です。

PID コントローラーは、専用のモデルオブジェクト pid2 および pidstd2 を使用して表現できます。このトピックでは、2-DOF PID コントローラーの MATLAB^® での表現について説明します。PID コントローラーの自動調整についての詳細は、PID コントローラーの調整を参照してください。

連続時間 2-DOF PID コントローラーの表現

次の図では、2-DOF PID コントローラーを使用した典型的な制御アーキテクチャが示されています。

2-DOF コントローラーの出力 (u) とその 2 つの入力 (r および y) との関係は、並列形式と標準形式のいずれかで表現できます。2 つの形式の違いは、次の表に示すように、コントローラーの比例動作、積分動作および微分動作の表現に使用されるパラメーターにあります。

形式式

形式	式
並列 (`pid2` オブジェクト)	$u = K_{p} (b r - y) + \frac{K_{i}}{s} (r - y) + \frac{K_{d} s}{T_{f} s + 1} (c r - y)$ この表現では以下のとおりです。 K_p = 比例ゲイン K_i = 積分ゲイン K_d = 微分ゲイン T_f = 微分フィルター時間 b = 比例項での設定点の重み c = 微分項での設定点の重み
標準 (`pidstd2` オブジェクト)	$u = K_{p} [(b r - y) + \frac{1}{T_{i} s} (r - y) + \frac{T_{d} s}{\frac{T_{d}}{N} s + 1} (c r - y)]$ この表現では以下のとおりです。 K_p = 比例ゲイン T_i = 積分時間 T_d = 微分時間 N = 微分フィルター除数 b = 比例項での設定点の重み c = 微分項での設定点の重み

並列 (pid2 オブジェクト)

$u = K_{p} (b r - y) + \frac{K_{i}}{s} (r - y) + \frac{K_{d} s}{T_{f} s + 1} (c r - y)$

この表現では以下のとおりです。

K_p = 比例ゲイン
K_i = 積分ゲイン
K_d = 微分ゲイン
T_f = 微分フィルター時間
b = 比例項での設定点の重み
c = 微分項での設定点の重み

標準 (pidstd2 オブジェクト)

$u = K_{p} [(b r - y) + \frac{1}{T_{i} s} (r - y) + \frac{T_{d} s}{\frac{T_{d}}{N} s + 1} (c r - y)]$

この表現では以下のとおりです。

K_p = 比例ゲイン
T_i = 積分時間
T_d = 微分時間
N = 微分フィルター除数
b = 比例項での設定点の重み
c = 微分項での設定点の重み

アプリケーションで使いやすいコントローラー形式を使用してください。たとえば、積分動作と微分動作を時定数で表現するのであれば、標準形式を使用します。並列形式コントローラーおよび標準形式コントローラーの作成方法を示す例は、それぞれ pid2 および pidstd2 のリファレンスページを参照してください。

離散時間での PID コントローラーの表現についての詳細は、離散時間比例-積分-微分 (PID) コントローラーを参照してください。

2-DOF 制御アーキテクチャ

2-DOF PID コントローラーは、次の図で示すような、C₂(s) の形式をもつ 2 入力 1 出力のコントローラーです。それぞれの入力からその出力までの伝達関数自体が PID コントローラーです。

コンポーネント C_r(s) および C_y(s) のそれぞれが、比例項および微分項に異なった重みをもつ PID コントローラーです。たとえば、連続時間において、これらのコンポーネントは次の式で与えられます。

$\begin{array}{l} C_{r} (s) = b K_{p} + \frac{K_{i}}{s} + \frac{c K_{d} s}{T_{f} s + 1}, \\ C_{y} (s) = - [K_{p} + \frac{K_{i}}{s} + \frac{K_{d} s}{T_{f} s + 1}] . \end{array}$

これらのコンポーネントには、PID コントローラーを 2 入力 1 出力の伝達関数に変換することによりアクセスできます。たとえば、C2 が 2-DOF PID コントローラーであり pid2 オブジェクトとして格納されているとします。

C2tf = tf(C2);
Cr = C2tf(1);
Cy = C2tf(2);

C_r(s) は、C2 の 1 番目の入力から出力への伝達関数です。同様に、C_y(s) は C2 の 2 番目の入力から出力への伝達関数です。

G が zpk モデルなどの動的システムモデルであり、プラントを表現している、とします。r から y への閉ループ伝達関数を作成します。C_y(s) の定義により、C_y(s) ループには正のフィードバックがあることに注意してください。

T = Cr*feedback(G,Cy,+1)

あるいは、connect コマンドを使用して、2-DOF コントローラー C2 を直接使った等価の閉ループシステムを作成します。これを行うには、G および C2 の InputName プロパティと OutputName プロパティを設定します。

G.InputName = 'u';
G.OutputName = 'y';
C2.Inputname = {'r','y'};
C2.OutputName = 'u';
T = connect(G,C2,'r','y');

この他にも、2-DOF PID コントローラーを SISO コンポーネントに分解できる構成があります。特定の C(s) および X(s) を選択すると、以下に挙げる構成のそれぞれが C₂(s) をもつ 2-DOF アーキテクチャと等価になります。これら各構成の C(s) と X(s) は、getComponents コマンドを使用して取得できます。

フィードフォワード

フィードフォワード構成において、2-DOF PID コントローラーは、エラー信号を入力として取る通常の SISO PID コントローラーとフィードフォワードコントローラーとに分解されます。

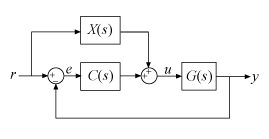
連続時間の並列形式 2-DOF PID コントローラーの場合、コンポーネントは次の式で与えられます。

$\begin{matrix} C (s) = K_{p} + \frac{K_{i}}{s} + \frac{K_{d} s}{T_{f} s + 1}, \\ X (s) = (b - 1) K_{p} + \frac{(c - 1) K_{d} s}{T_{f} s + 1} . \end{matrix}$

これらのコンポーネントには、getComponents を使用してアクセスします。

[C,X] = getComponents(C2,'feedforward');

次のコマンドは、フィードフォワード構成に合わせて r から y までの閉ループシステムを構成します。

T = G*(C+X)*feedback(1,G*C);

フィードバック

フィードバック構成において、2-DOF PID コントローラーは通常の SISO PID コントローラーとフィードバックコントローラーとに分解されます。

連続時間の並列形式 2-DOF PID コントローラーの場合、コンポーネントは次の式で与えられます。

$\begin{matrix} C (s) = b K_{p} + \frac{K_{i}}{s} + \frac{c K_{d} s}{T_{f} s + 1}, \\ X (s) = (1 - b) K_{p} + \frac{(1 - c) K_{d} s}{T_{f} s + 1} . \end{matrix}$

これらのコンポーネントには、getComponents を使用してアクセスします。

[C,X] = getComponents(C2,'feedback');

次のコマンドは、フィードバック構成に合わせて r から y までの閉ループシステムを構成します。

T = G*C*feedback(1,G*(C+X));

フィルター

フィルター構成において、2-DOF PID コントローラーは通常の SISO PID コントローラーと基準信号のプレフィルターとに分解されます。

連続時間の並列形式 2-DOF PID コントローラーの場合、コンポーネントは次の式で与えられます。

$\begin{matrix} C (s) = K_{p} + \frac{K_{i}}{s} + \frac{K_{d} s}{T_{f} s + 1}, \\ X (s) = \frac{(b K_{p} T_{f} + c K_{d}) s^{2} + (b K_{p} + K_{i} T_{f}) s + K_{i}}{(K_{p} T_{f} + K_{d}) s^{2} + (K_{p} + K_{i} T_{f}) s + K_{i}} . \end{matrix}$