位相変調

位相変調 (PM) は線形ベースバンド変調方式で、この手法ではメッセージにより定振幅信号の位相を変調します。Communications Toolbox™ ソフトウェアには、以下の関数、System object、およびブロックが含まれており、以下の変調方式でデジタル ベースバンド信号を変調します。

• 2 位相、直交位相、および一般的な位相偏移変調 (PSK)

• 2 位相、直交位相、および一般的な差動位相偏移変調 (DPSK)

• オフセット直交位相偏移変調 (OQPSK)

関数	System object	ブロック
dpskmod, dpskdemod pskmod, pskdemod	comm.DBPSKModulator, comm.DBPSKDemodulator comm.DPSKModulator, comm.DPSKDemodulator comm.DQPSKModulator, comm.DQPSKDemodulator comm.OQPSKModulator, comm.OQPSKDemodulator comm.gpu.PSKModulator, comm.gpu.PSKDemodulator	BPSK Modulator Baseband, BPSK Demodulator Baseband DBPSK Modulator Baseband, DBPSK Demodulator Baseband DQPSK Modulator Baseband, DQPSK Demodulator Baseband M-DPSK Modulator Baseband, M-DPSK Demodulator Baseband M-PSK Modulator Baseband, M-PSK Demodulator Baseband OQPSK Modulator Baseband, OQPSK Demodulator Baseband QPSK Modulator Baseband, QPSK Demodulator Baseband

BPSK

位相変調は線形ベースバンド変調手法で、この手法ではメッセージにより定振幅信号の位相を変調します。2 相位相偏移変調 (BPSK) は 2 つの位相の変調スキームであり、バイナリ メッセージの 0 と 1 は次の搬送信号において 2 つの異なる位相状態で表されます。

$$s_n(t)=\sqrt{\frac{2E_b}{T_b}}\cos \left(2\pi f_{c}t+{\varphi }_n\right),$$

このとき、$$(n-1)T_b\le t\le n{T}_b,\text{ n}=\text{1},\text{2},\text{ 3},\dots$$ です。各項目の意味は次のとおりです。

• ϕ_n = πm + ϕ, m∈{0,1}。

• ϕ は初期位相オフセットです。

• E_b はビットあたりのエネルギーです。

• T_b はビットの持続時間です。

• f_c は搬送波周波数です。

MATLAB^® では、BPSK 信号のベースバンド表現は次のようになります。

$$s_n(t)=e^{-i{\varphi }_n}=\cos \left(\pi n\right).$$

BPSK 信号は 2 つの位相をもちます。0 と π です。

AWGN チャネルのビット エラーの確率は次のようになります。

$$P_b=Q\left(\sqrt{\frac{2E_b}{N_0}}\right),$$

ここで、N₀ はノイズ パワー スペクトル密度です。

QPSK

直交位相偏移変調では、メッセージ ビットが 2 ビット シンボルにグループ分けされ、定振幅ベースバンド信号の 4 つの位相の 1 つとして送信されます。このグループ分けにより、帯域幅の効率が BPSK の効率の 2 倍になります。一般的な QPSK 信号は次のように表現されます。

$$s_m(t)=\sqrt{\frac{2E_s}{T_s}}\cos \left(2\pi f_{c}t+\frac{2\pi m}{4}+\varphi \right);m\in \{0,1,2,3\},$$

ここで、E_s はシンボルあたりのエネルギー、T_s はシンボルの持続時間、ϕ は初期位相オフセットです。QPSK 信号の複素ベースバンドの表現は次のようになります。

$$s_m(t)=\exp \left(j\left(\frac{2\pi m}{4}+\varphi \right)\right);m\in \{0,1,2,3\}.$$

この QPSK コンスタレーション ダイアグラムでは、各 2 ビット シーケンスが 4 つの可能な状態の 1 つにマッピングされます。状態は位相 π/4、3π/4、5π/4、および 7π/4 に対応します。

ビット エラー レートのパフォーマンスを向上させるために、受信ビットをグレイ符号順にマッピングできます。グレイ符号化の主な利点は、隣接するコンスタレーション点の間の移動では、2 ビットのうち 1 つのみが変更されることです。次の表では、バイナリ マッピングとグレイ マッピングについて、コンスタレーション点のシーケンスを比較しています。

バイナリ符号化シーケンス	グレイ符号化シーケンス
00	00
01	01
10	11
11	10

グレイ符号化は高次の変調に適用できます。次に、グレイ符号化された QPSK コンスタレーションを示します。

グレイ符号化を使用した場合、AWGN 環境下での QPSK のビット エラー確率は次のようになります。

$$P_b=Q\left(\sqrt{\frac{2E_b}{N_0}}\right),$$

これは BPSK の式と同じです。結果として、QPSK は帯域幅の効率の 2 倍と同等のパフォーマンスになります。

高次 PSK

高次の PSK コンスタレーションの場合、バイナリ順序のシンボル マッピングを使用した M-ary PSK 信号の複素ベースバンド形式は次のようになります。

$$s_m(t)=\exp \left(j\left(\frac{2\pi m}{M}+\varphi \right)\right);m\in \{0,1,\dots ,M-1\}.$$

入力がビット用に構成されている場合、log₂(M) ビットのグループが、構成されたシンボル マッピングの複素シンボルを表します。マッピングは、バイナリ符号化、グレイ符号化、またはカスタム符号化できます。

グレイ符号化には、隣接するコンスタレーション点間で変化するビットが 1 つだけであるという利点があるため、ビット エラー レート性能が向上します。

この 8-PSK コンスタレーションではグレイ符号化されたシンボル マッピングが使用されます。

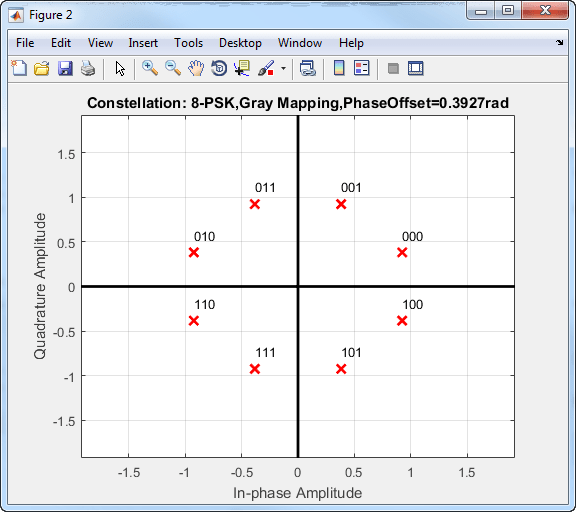
4 を超える変調次数の場合、AWGN 環境下での PSK のビット エラー レートのパフォーマンスが低下します。このグレイ符号化されたマッピングのビット エラー レート プロットでは、QPSK と BPSK の曲線が相互に重なり合っています。

DPSK

DPSK は位相偏移変調の非コヒーレントな形式で、受信機にコヒーレントな基準信号は必要ありません。DPSK の場合、連続した入力シンボルの間の差が特定の位相にマッピングされます。例として、バイナリ DPSK (DBPSK) の場合、変調スキームは、連続ビット間の差が 0 または 1 のバイナリにマッピングされるように動作します。入力ビットが 1 の場合、差動符号化されたシンボルは前のシンボルと同じままですが、0 を受信すると、出力シンボルが切り替わります。

DPSK のデメリットは、エネルギー効率がコヒーレント PSK を約 3 dB 下回ることです。AWGN 環境下での DBPSK のビット エラー確率は、P_b = 1/2 exp(E_b/N₀) です。

OQPSK

オフセット QPSK は QPSK に似ていますが、同相ビット ストリームと直交ビット ストリームの時間の調節法が異なります。QPSK の場合、同相ビット ストリームと直交ビット ストリームが同時に遷移します。OQPSK の場合、次のように遷移にシンボル周期の半分のオフセットが含まれます。

同相信号と直交信号の遷移は、シンボル間の境界でのみ発生します。サンプル レートが 1 Hz であるため、この遷移は 1 秒間隔で発生します。次の図は、OQPSK 信号の同相信号と直交信号を示しています。

OQPSK の場合、直交信号にはシンボル周期の 1/2 (0.5 秒) のオフセットが含まれます。

AWGN 環境下での OQPSK 信号の BER は、QPSK 信号のものと同一です。BER は次のようになります。

$$P_b=Q\left(\sqrt{\frac{2E_b}{N_0}}\right),$$

ここで、E_b はビットあたりのエネルギー、N₀ はノイズ パワー スペクトル密度です。

参照

[1] Rappaport, Theodore S. Wireless Communications: Principles and Practice. Upper Saddle River, NJ: Prentice Hall, 1996.

[2] Viterbi, A.J. “An Intuitive Justification and a Simplified Implementation of the MAP Decoder for Convolutional Codes.” IEEE^® Journal on Selected Areas in Communications 16, no. 2 (February 1998): 260–64. https://doi.org/10.1109/49.661114.

参考

関数

• rcosdesign

オブジェクト

• comm.RaisedCosineTransmitFilter | comm.RaisedCosineReceiveFilter

ブロック

• Raised Cosine Transmit Filter | Raised Cosine Receive Filter | Bipolar to Unipolar Converter | Unipolar to Bipolar Converter | Data Mapper

トピック

• 位相変調の例
• リード・ソロモン符号化を使用した AWGN 環境下での QPSK の BER 推定
• 対数尤度比 (LLR) 復調
• ベースバンド デジタル変調