このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

pskdemod

M-ary PSK 手法を使用した復調

構文

z = pskdemod(y,M)

z = pskdemod(y,M,phaseoffset)

z = pskdemod(y,M,phaseoffset,symorder)

z = pskdemod(y,M,Name=Value)

説明

z = pskdemod(y,M) は、入力 M-PSK 信号 y を復調します。M は変調次数を指定します。

z = pskdemod(y,M,phaseoffset) は、M-PSK コンスタレーションの位相オフセットを指定します。

z = pskdemod(y,M,phaseoffset,symorder) は、M-PSK コンスタレーションのシンボル順序を指定します。

z = pskdemod(y,M,Name=Value) は、名前と値の引数を使用してオプションを指定します。

例

PSK および PAM 信号への位相ノイズの影響の比較

PSK と PAM の変調方式を比較し、PSK の方が位相ノイズの影響を受けやすいことを示します。PSK の方が位相ノイズの影響を受けやすいのは、PAM コンスタレーションが線形であるのに対し PSK コンスタレーションが円形であるためです。

シンボル数と変調次数のパラメーターを指定します。ランダム データ シンボルを生成します。

len = 10000;                
M = 16;                     
msg = randi([0 M-1],len,1);

位相ノイズ System object™ を作成し、構成された設定を表示します。

phasenoise = comm.PhaseNoise(Level=[-70 -80])

phasenoise = 
  comm.PhaseNoise with properties:

              Level: [-70 -80]
    FrequencyOffset: [2000 20000]
         SampleRate: 1000000
       RandomStream: 'Global stream'

PSK と PAM の両方を使用して msg を変調し、2 つの方法を比較します。

txpsk = pskmod(msg,M);
txpam = pammod(msg,M);

変調された信号の位相をずらします。

rxpsk = phasenoise(txpsk);
rxpam = phasenoise(txpam);

受信信号の散布図を作成します。

scatterplot(rxpsk);
title('Noisy PSK Scatter Plot')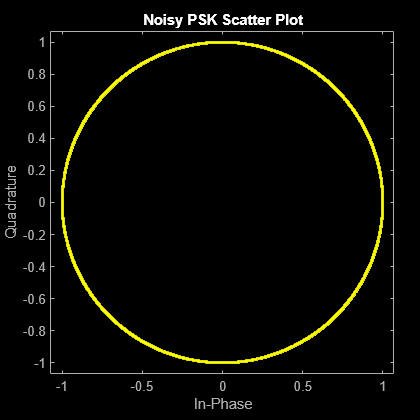

scatterplot(rxpam);
title('Noisy PAM Scatter Plot')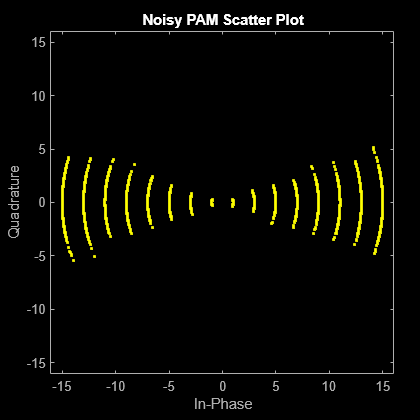

受信信号を復調します。

recovpsk = pskdemod(rxpsk,M);
recovpam = pamdemod(rxpam,M);

それぞれの変調方式のシンボル誤りの数を計算します。PSK 信号の場合、かなり多数のシンボル誤りが発生します。

numerrs_psk = symerr(msg,recovpsk);
numerrs_pam = symerr(msg,recovpam);
[numerrs_psk numerrs_pam]

ans = 1×2

   286     1

AWGN の QPSK 信号の変調と復調

ランダムなシンボルを生成します。

dataIn = randi([0 3],1000,1);

データを QPSK 変調します。

txSig = pskmod(dataIn,4,pi/4);

AWGN チャネルを通して信号を渡します。

rxSig = awgn(txSig,10);

受信信号を復調し、シンボル誤りの数を計算します。

dataOut = pskdemod(rxSig,4,pi/4);
numErrs = symerr(dataIn,dataOut)

numErrs = 2

PSK シンボル マッピング

変調次数を設定し、コンスタレーション点の完全なセットを含むデータ シーケンスを作成します。

M = 8;
data = (0:M-1);
phaseoffset = 0;

変調および復調されたグレイ バイナリ符号化データと通常のバイナリ符号化データに対する 8-PSK シンボル マッピングのプロット コンスタレーションを可視化します。

symgray = pskmod(data,M,phaseoffset,'gray',PlotConstellation=true, ...
          InputType='integer');

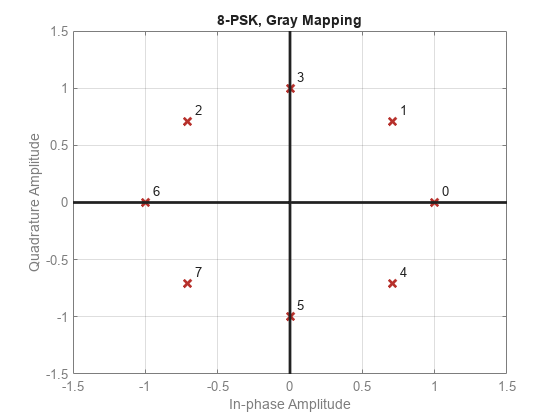
mapgray = pskdemod(symgray,M,phaseoffset,'gray',OutputType='integer');
symbin = pskmod(data,M,phaseoffset,'bin');
mapbin = pskdemod(symbin,M,phaseoffset,'bin',PlotConstellation=true, ...
         OutputType='bit');

入力引数

y — M-PSK 変調された入力信号

スカラー | ベクトル | 行列

M-PSK 変調された入力信号。スカラー、ベクトルまたは行列として指定します。y が行列の場合、関数は列を個別に処理します。

データ型: double | single
複素数のサポート: あり

M — 変調次数

1 より大きい整数値

変調次数。1 より大きい整数値として指定します。

データ型: double

phaseoffset — Phase offset

0 (既定値) | スカラー

PSK コンスタレーションの位相オフセット (ラジアン単位)。スカラーとして指定します。

データ型: double

symorder — シンボルの順序

'gray' (既定値) | 'bin' | ベクトル

シンボルの順序。'gray'、'bin'、またはベクトルとして指定します。この引数は、どのようにバイナリ ベクトルを対応する整数に割り当てるかを指定します。

• 'gray' — グレイ符号化された順序を使用します。

• 'bin' — 通常の 2 値符号の順序を使用します。

• ベクトル –– カスタムのシンボル順序を使用します。ベクトルの長さは M で、範囲 [0, M – 1] 内の一意の値を含みます。最初の要素は、角度 phaseoffset に対応するコンスタレーション点に相関し、続く要素は反時計回りに実行されます。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値の各ペアを区切り、Name を引用符で囲みます。

例: y = pskdemod(x,M,phaseoffset,symorder,OutputType='bit')

OutputType — 出力のタイプ

'integer' (既定値) | 'bit' | 'llr' | 'approxllr'

出力のタイプ。'integer'、'bit'、'llr' または 'approxllr' として指定します。

OutputDataType — 出力のデータ型

'double' | 'single' | ...

出力データ型。次のいずれかとして指定します。

OutputType の値	使用可能な OutputDataType の値
'integer'	'double'、'single'、'int8'、'int16'、'int32'、'uint8'、'uint16' または 'uint32'
'bit'	'double'、'single'、'int8'、'int16'、'int32'、'uint8'、'uint16'、'uint32' または 'logical'

既定値は、入力 y のデータ型になります。

依存関係

この引数を有効にするには、引数 OutputType を 'integer' または 'bit' に設定します。そうでない場合、出力のデータ型は、入力 y のデータ型と同じになります。

NoiseVariance — ノイズ分散

1 (既定値) | 正のスカラー | 正の値のベクトル

ノイズ分散。次のいずれかのオプションとして指定します。

• 正のスカラー — すべての入力要素で同じノイズ分散値を使用します。

• 正の値のベクトル — ベクトルの各要素によって指定された、対応する最後の次元に沿った入力のすべての要素でノイズ分散を使用します。ベクトルの長さは入力信号の最後の次元の要素数に等しくなければなりません。

ヒント

厳密な LLR アルゴリズムは有限の精度演算で指数を計算します。計算に非常に大きな正または負の振幅が含まれる場合、厳密な LLR アルゴリズムの結果は次のようになります。

• ノイズ分散が極度に大きい値の場合は、Inf または -Inf

• ノイズ分散と信号強度の両方が非常に小さい値の場合は NaN

近似 LLR アルゴリズムでは指数が計算されません。近似 LLR アルゴリズムを使用することによって、Inf、-Inf、および NaN の結果を回避できます。

依存関係

この引数を有効にするには、引数 OutputType を 'llr' または 'approxllr' に設定します。

データ型: double

PlotConstellation — コンスタレーションをプロットするためのオプション

false または 0 (既定値) | true または 1

コンスタレーションをプロットするためのオプション。logical 0 (false) または logical 1 (true) として指定します。PSK コンスタレーションをプロットするには、'PlotConstellation' を true に設定します。

出力引数

z — M-PSK 復調された出力信号

スカラー | ベクトル | 行列

M-PSK 復調された出力信号。スカラー、または入力信号 y と同じ列数のベクトルまたは行列として返されます。この出力の値と次元は、次の表に示すように、指定した 'OutputType' 値によって異なります。

'OutputType'	pskdemod の出力値	出力の次元
'integer'	復調した整数値 ([0, M – 1] の範囲)	z の次元は入力 y と同じになります。
'bit'	復調されたビット	z の行数は、y の行数の log2(M) 倍になります。関数は復調された各シンボルを log2(M) ビットのグループにマッピングします。ここで、最初のビットは最上位ビット (MSB) を表し、最後のビットは最下位ビット (LSB) を表します。
'llr'	厳密な対数尤度アルゴリズムを使用して計算された各ビットの対数尤度比の値。詳細は、厳密な LLR アルゴリズムを参照してください。
'approxllr'	各ビットの近似対数尤度比の値。この値は近似対数尤度アルゴリズムを使用して計算されます。詳細については、近似 LLR アルゴリズムを参照してください。

参照

[1] Proakis, John G. Digital Communications. 4th ed. New York: McGraw Hill, 2001.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

R2006a より前に導入

R2022a: 関数に対する新たな拡張

以下のことができるようになりました。

• 引数 OutputType によるバイナリ出力の指定。

• 引数 symorder によるカスタム シンボル マッピングの指定。既定は今後 'gray' シンボル マッピングになります。

• ビット単位の対数尤度アルゴリズムまたは近似対数尤度アルゴリズムを使用した軟判定復調の実行

• 引数 OutputDataType によるすべての組み込み数値データ型の指定。

• 引数 PlotConstellation による基準コンスタレーションの可視化。

参考

pskmod | qamdemod | apskdemod | dvbsapskdemod | mil188qamdemod

トピック

• 位相変調
• 硬判定復調と軟判定復調

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい