comm.RaisedCosineTransmitFilter

レイズドコサイン FIR フィルターを使用した信号の内挿によるパルス整形の適用

説明

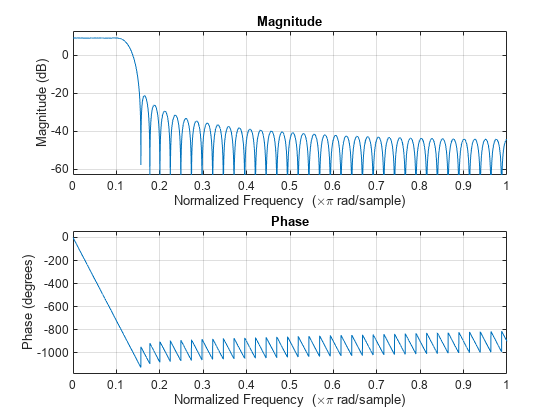
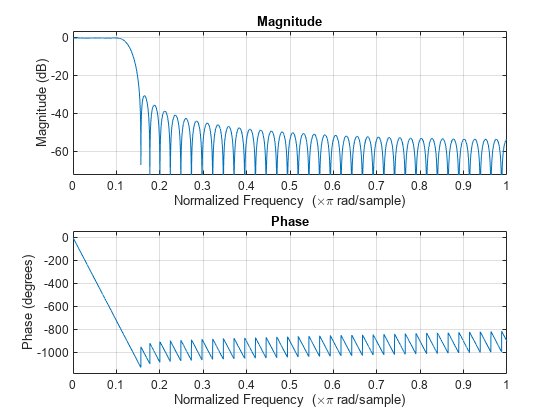
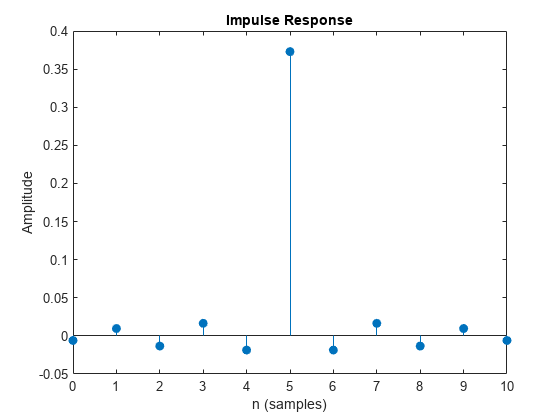
comm.RaisedCosineTransmitFilter System object™ は、レイズドコサイン有限インパルス応答 (FIR) フィルターを使用して、入力信号を内挿することによってパルス整形を適用します。FIR フィルターは、(FilterSpanInSymbols × OutputSamplesPerSymbol + 1) タップ係数をもちます。

レイズドコサイン FIR フィルターを使用して入力信号を内挿してパルス整形を適用するには、次のようにします。

comm.RaisedCosineTransmitFilter オブジェクトを作成し、そのプロパティを設定します。
関数と同様に、引数を指定してオブジェクトを呼び出します。

System object の機能の詳細については、System object とはを参照してください。

作成

構文

txfilter = comm.RaisedCosineTransmitFilter

txfilter = comm.RaisedCosineTransmitFilter(Name,Value)

説明

txfilter = comm.RaisedCosineTransmitFilter は、レイズドコサイン FIR フィルターを使用して入力信号を内挿する、レイズドコサイン送信 FIR フィルター System object を返します。このフィルターは、効率的なポリフェーズ FIR 内挿構造体を使用し、ユニットエネルギーをもちます。

例

txfilter = comm.RaisedCosineTransmitFilter(Name,Value) は、1 つ以上の名前と値のペアを使用してプロパティを設定します。各プロパティ名を引用符で囲みます。たとえば、comm.RaisedCosineTransmitFilter('FilterSpanInSymbols',15) では、フィルタースパンが 15 シンボルに設定されたレイズドコサイン送信フィルター System object が設定されます。

プロパティ

すべて展開する

特に指定がない限り、プロパティは "調整不可能" です。つまり、オブジェクトの呼び出し後に値を変更することはできません。オブジェクトは呼び出すとロックされ、ロックを解除するには関数 release を使用します。

プロパティが "調整可能" の場合、その値をいつでも変更できます。

プロパティ値の変更の詳細については、System object を使用した MATLAB でのシステム設計を参照してください。

`Shape` — Filter shape
`'Square root'` (既定値) | `'Normal'`

フィルターの形状。'Square root' または 'Normal' として指定します。

データ型: char | string

`RolloffFactor` — ロールオフ係数
`0.2` (既定値) | 範囲 [0,1] のスカラー

ロールオフ係数。範囲が [0, 1] のスカラーとして指定します。

データ型: double

`FilterSpanInSymbols` — Filter span in symbols
`10` (既定値) | 正の整数

シンボル内のフィルタースパン。正の整数として指定します。オブジェクトは理想のレイズドコサインフィルターの無限インパルス応答 (IIR) を、このプロパティで指定されるシンボル数をカバーするインパルス応答に打ち切ります。

データ型: double

`OutputSamplesPerSymbol` — Output samples per symbol
`8` (既定値) | 正の整数

シンボルあたりの出力サンプル数。正の整数として指定します。

データ型: double

`Gain` — 線形フィルターゲイン
`1` (既定値) | 正のスカラー

線形フィルターゲイン。正のスカラーとして指定します。オブジェクトは、ユニットエネルギーをもつレイズドコサインフィルターを設計し、線形フィルターゲインを適用して最終タップ係数値を取得します。

データ型: double

使用法

構文

y = txfilter(x)

説明

例

y = txfilter(x) は、レイズドコサイン FIR フィルターを使用して入力信号を内挿してパルス整形を適用します。出力は、内挿後の信号の値で構成されます。

入力引数

すべて展開する

`x` — 入力信号
列ベクトル | 行列

入力信号。列ベクトルまたは K_i 行 N 列の行列として指定します。K_i は信号チャネルあたりの入力サンプル数、N は信号チャネルの数です。

K_i 行 N 列の行列入力の場合、オブジェクトは、入力行列の列を N 個の独立したチャネルとして扱います。

データ型: double | single
複素数のサポート: あり

出力引数

すべて展開する

`y` — 出力信号
列ベクトル | 行列

出力ベクトル。K_o 行 N 列の行列として指定します。K_o は K_i × OutputSamplesPerSymbol と等しくなります。K_i は信号チャネルあたりの入力サンプル数、N は信号チャネルの数です。

オブジェクトは、1 番目の次元全体で各チャネルを内挿およびフィルター処理し、K_o 行 N 列の出力行列を生成します。出力信号のデータ型は、入力信号のデータ型と同じです。

オブジェクト関数

オブジェクト関数を使用するには、System object を最初の入力引数として指定します。たとえば、obj という名前の System object のシステムリソースを解放するには、次の構文を使用します。

release(obj)

すべて展開する

`comm.RaisedCosineTransmitFilter` に固有

`info`	フィルター System object に関する情報
`coeffs`	フィルターの係数
`cost`	Computational cost of implementing filter System object
`freqz`	離散時間フィルターの周波数応答
`fvtool`	フィルターの周波数応答のプロット
`grpdelay`	Group delay response of discrete-time filter
`impz`	離散時間フィルターのインパルス応答
`order`	離散時間フィルター System object の次数

すべての System object に共通

`step`	System object のアルゴリズムの実行
`release`	リソースを解放し、System object のプロパティ値と入力特性の変更を可能にします。
`reset`	System object の内部状態のリセット

例

すべて折りたたむ

ルートレイズドコサインフィルターを使用した信号の内挿

ライブスクリプトを開く

ルートレイズドコサイン (SRRC) 送信フィルターオブジェクトを使用して信号を内挿し、フィルター処理された信号のスペクトルを表示します。

1 秒あたり 1e6 シンボルのシンボルレートでランダムなバイポーラシンボルを作成します。

data = 2*randi([0 1],1e6,1) - 1;

SRRC 送信フィルターオブジェクトを作成します。既定では、フィルターが平方根の形状に設定され、シンボルあたりのサンプル数が 8 に設定されます。

txfilter = comm.RaisedCosineTransmitFilter

txfilter = 
  comm.RaisedCosineTransmitFilter with properties:

                     Shape: 'Square root'
             RolloffFactor: 0.2000
       FilterSpanInSymbols: 10
    OutputSamplesPerSymbol: 8
                      Gain: 1

SRRC フィルターを使ってデータをフィルター処理します。

filteredData = txfilter(data);

8e6 サンプリングレートでスペクトルアナライザーオブジェクトを作成します。このサンプリングレートは、フィルター処理された信号のサンプリングレートと一致します。

spectrumAnalyzer = spectrumAnalyzer(SampleRate=8e6);

スペクトルアナライザーオブジェクトを使用して、フィルター処理された信号のスペクトルを表示します。

spectrumAnalyzer(filteredData)
release(spectrumAnalyzer)

振幅応答へのフィルタースパンの影響の調査

ライブスクリプトを開く

さまざまなフィルタースパンでルートレイズドコサイン (SRRC) フィルターから内挿された信号を作成します。さまざまなフィルター設計の振幅応答を調査します。

さまざまなフィルタースパンを設定する SRRC フィルターオブジェクトを作成します。オブジェクト関数coeffsを使用して、フィルター係数を取得します。

txfilt2 = comm.RaisedCosineTransmitFilter('FilterSpanInSymbols',2);
txfilt4 = comm.RaisedCosineTransmitFilter('FilterSpanInSymbols',4);
txfilt6 = comm.RaisedCosineTransmitFilter('FilterSpanInSymbols',6);
txfilt8 = comm.RaisedCosineTransmitFilter('FilterSpanInSymbols',8);
txfilt16 = comm.RaisedCosineTransmitFilter('FilterSpanInSymbols',16);

taps2 = coeffs(txfilt2).Numerator;
taps4 = coeffs(txfilt4).Numerator;
taps6 = coeffs(txfilt6).Numerator;
taps8 = coeffs(txfilt8).Numerator;
taps16 = coeffs(txfilt16).Numerator;

フィルターの可視化ツールを起動して、さまざまなフィルタースパンの振幅応答を表示します。サンプルレートを 1 kHz に指定します。中央揃えの両側応答を表示します。

fvt = fvtool(taps2,1,taps4,1,taps8,1,taps16,1);
fvt.Fs = 1e3;
fvt.FrequencyRange = '[-Fs/2, Fs/2)';
legend(fvt,'Span 2 symbols','Span 4 symbols', ...
    'Span 8 symbols','Span 10 symbols')

Figure Figure 1: Magnitude Response (dB) contains an axes object. The axes object with title Magnitude Response (dB), xlabel Frequency (Hz), ylabel Magnitude (dB) contains 4 objects of type line. These objects represent Span 2 symbols, Span 4 symbols, Span 8 symbols, Span 10 symbols.

1 の通過帯域ゲインをもつルートレイズドコサイン送信フィルターの作成

ライブスクリプトを開く

ルートレイズドコサイン (SRRC) 送信フィルター System object™ を作成してから、フィルター応答をプロットします。結果には、線形フィルターゲインが 1 より大きいことが示されます。特に、通過帯域ゲインは 0 dB より大きくなります。

txfilter = comm.RaisedCosineTransmitFilter;
fvtool(txfilter)

Figure Figure 1: Magnitude Response (dB) contains an axes object. The axes object with title Magnitude Response (dB), xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Magnitude (dB) contains an object of type line.

オブジェクト関数coeffsを使用してフィルター係数を取得し、フィルターゲインをユニットエネルギーに合わせて調整します。

b = coeffs(txfilter);

1 の通過帯域ゲインをもつフィルターは、合計が 1 になるようなフィルター係数をもたなければならないため、線形フィルターゲインをフィルタータップ係数 b.Numerator の合計の逆数に設定します。

txfilter.Gain = 1/sum(b.Numerator);

結果のフィルター係数の合計が 1 になることを確認します。

bNorm = coeffs(txfilter);
sum(bNorm.Numerator)

ans = 1.0000

フィルターの周波数応答をもう一度プロットします。結果には通過帯域ゲインが 0 dB (1 のゲイン) であることが示されます。

fvtool(txfilter)

Figure Figure 2: Magnitude Response (dB) contains an axes object. The axes object with title Magnitude Response (dB), xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Magnitude (dB) contains an object of type line.

RRC フィルターのポリフェーズ行列の確認

ライブスクリプトを開く

ポリフェーズ分解を使用するマルチレートフィルターを作成する場合、関数 polyphase を使用すると、成分を行列の行として返して成分のフィルターを個別に解析できます。出力引数を指定して polyphase を使用すると、行単位でサブフィルターが定義されたポリフェーズ分解を含む行列が返されます。

rcfilter = comm.RaisedCosineTransmitFilter;
p = polyphase(rcfilter)

p = 8×11

   -0.0060    0.0097   -0.0133    0.0165   -0.0186    0.3729   -0.0186    0.0165   -0.0133    0.0097   -0.0060
   -0.0051    0.0058   -0.0041   -0.0029    0.0297    0.3621   -0.0524    0.0301   -0.0190    0.0112         0
   -0.0029   -0.0000    0.0075   -0.0255    0.0892    0.3308   -0.0707    0.0368   -0.0206    0.0105         0
    0.0004   -0.0068    0.0196   -0.0477    0.1552    0.2823   -0.0742    0.0364   -0.0184    0.0079         0
    0.0043   -0.0134    0.0300   -0.0653    0.2218    0.2218   -0.0653    0.0300   -0.0134    0.0043         0
    0.0079   -0.0184    0.0364   -0.0742    0.2823    0.1552   -0.0477    0.0196   -0.0068    0.0004         0
    0.0105   -0.0206    0.0368   -0.0707    0.3308    0.0892   -0.0255    0.0075   -0.0000   -0.0029         0
    0.0112   -0.0190    0.0301   -0.0524    0.3621    0.0297   -0.0029   -0.0041    0.0058   -0.0051         0

出力引数を指定せずに polyphase を使用すると、フィルターの可視化ツールが開き、ツールの解析機能を使用してフィルターの調査をすぐに開始できます。FVTool を使用したフィルター解析には、サブフィルターの係数が表示されます。サブフィルターの振幅応答を表示するには、FVTool を使用したフィルター解析のツールストリップで [Magnitude Response] ボタンをクリックします。

polyphase(rcfilter)

Figure Figure 1: Filter Coefficients contains an object of type uilistbox.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

MATLAB コード生成における System object (MATLAB Coder)を参照してください。

comm.RaisedCosineTransmitFilter System object は、次の条件下で Intel AVX2 テクノロジーを使用した SIMD コード生成をサポートします。

入力信号は、実数フィルター係数を使用する場合、実数値である。
入力信号が実数または複素数のフィルター係数をもつ複素数値である。
入力信号のデータ型が single または double である。

SIMD テクノロジーにより、生成コードのパフォーマンスが大幅に向上します。詳細については、Generate SIMD Code from MATLAB Functions for Intel Platforms (Embedded Coder)を参照してください。

バージョン履歴

R2013b で導入

参考

オブジェクト

comm.RaisedCosineReceiveFilter | dsp.FIRInterpolator | dsp.FIRDecimator

関数

rcosdesign

comm.RaisedCosineTransmitFilter

説明

作成

構文

説明

プロパティ

Shape — Filter shape 'Square root' (既定値) | 'Normal'

RolloffFactor — ロールオフ係数 0.2 (既定値) | 範囲 [0,1] のスカラー

FilterSpanInSymbols — Filter span in symbols 10 (既定値) | 正の整数

OutputSamplesPerSymbol — Output samples per symbol 8 (既定値) | 正の整数

Gain — 線形フィルター ゲイン 1 (既定値) | 正のスカラー

使用法

構文

説明

入力引数

x — 入力信号 列ベクトル | 行列

出力引数

y — 出力信号 列ベクトル | 行列

オブジェクト関数

comm.RaisedCosineTransmitFilter に固有

すべての System object に共通

例

ルート レイズド コサイン フィルターを使用した信号の内挿

振幅応答へのフィルター スパンの影響の調査

1 の通過帯域ゲインをもつルート レイズド コサイン送信フィルターの作成

RRC フィルターのポリフェーズ行列の確認

拡張機能

C/C++ コード生成 MATLAB® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

参考

オブジェクト

関数

`Shape` — Filter shape
`'Square root'` (既定値) | `'Normal'`

`RolloffFactor` — ロールオフ係数
`0.2` (既定値) | 範囲 [0,1] のスカラー

`FilterSpanInSymbols` — Filter span in symbols
`10` (既定値) | 正の整数

`OutputSamplesPerSymbol` — Output samples per symbol
`8` (既定値) | 正の整数

`Gain` — 線形フィルターゲイン
`1` (既定値) | 正のスカラー

`x` — 入力信号
列ベクトル | 行列

`y` — 出力信号
列ベクトル | 行列

`comm.RaisedCosineTransmitFilter` に固有

ルートレイズドコサインフィルターを使用した信号の内挿

振幅応答へのフィルタースパンの影響の調査

1 の通過帯域ゲインをもつルートレイズドコサイン送信フィルターの作成

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。