通信システムにおけるフィルター処理

Communications Toolbox™ でサポートされるフィルター処理タスクには次が含まれます。

以下の図で示される、レイズドコサインフィルターを使用したパルス整形および整合フィルター処理。
非線形増幅器に起因する符号間干渉 (ISI) の低減。
理想的な矩形パルスを使用した信号の整形。
積分とダンプ操作またはウィンドウを適用した積分器の実装。送信機において理想的な矩形パルスモデルが使用されたときに、受信機において積分とダンプ操作がよく使用されます。積分とダンプは、光ファイバー、および CDMA (コード分割多重アクセス) アプリケーションなどのスペクトル拡散通信システムでも使用できます。

フィルター処理の他の機能については、デジタルフィルターとアナログフィルターとフィルターの設計と解析を参照してください。

レイズドコサインフィルターは、伝播遅延がなく、非因果性です。これは、現在の出力がシステムへの将来の入力に依存することを意味します。"実現可能な" フィルターだけを設計するために、実装では出力を生成する前にピーク応答を遅延させます。フィルターの "群遅延" として知られるこの遅延は、フィルターの初期応答とピーク応答の間の時間です。シンボルのフィルタースパンは、シンボルの群遅延の 2 倍です。詳細については、群遅延を参照してください。

フィルターおよびパルス整形の予備的な情報については、参照を参照してください。

レイズドコサインフィルター System object を使ったパルス整形

ライブスクリプトを開く

対になるルートレイズドコサイン整合フィルター処理を使用して 16-QAM 信号のフィルター処理を行います。信号のアイダイアグラムおよび散布図をプロットします。AWGN チャネル経由で信号を渡した後にビットエラー数を計算します。

シミュレーションとフィルターのパラメーターを設定します。

M = 16;         % Modulation order
bps = log2(M);  % Bits per symbol
n = 20000;      % Transmitted bits
sps = 4;        % Samples per symbol
EbNo = 10;      % Eb/N0 (dB)
span = 10;      % Filter span in symbols
rolloff = 0.25; % Filter rolloff factor

定義したパラメーターを使用して、レイズドコサイン送信フィルターオブジェクトおよびレイズドコサイン受信フィルターオブジェクトを作成します。

txfilter = comm.RaisedCosineTransmitFilter( ...
    RolloffFactor=rolloff, ...
    FilterSpanInSymbols=span, ...
    OutputSamplesPerSymbol=sps);

rxfilter = comm.RaisedCosineReceiveFilter( ...
    RolloffFactor=rolloff, ...
    FilterSpanInSymbols=span, ...
    InputSamplesPerSymbol=sps, ...
    DecimationFactor=sps);

レイズドコサイン送信フィルターオブジェクト txFilter のインパルス応答をプロットします。

impz(txfilter.coeffs.Numerator)

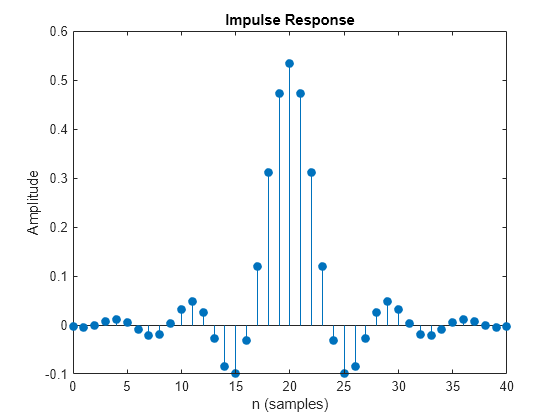
Figure contains an axes object. The axes object with title Impulse Response, xlabel n (samples), ylabel Amplitude contains an object of type stem.

整合フィルターによる遅延を計算します。群遅延は、1 つのフィルター全体のフィルタースパンの半分であるため、両方のフィルターのフィルタースパンと等しくなります。シンボルあたりのビット数を掛けてビット単位の遅延を取得します。

filtDelay = bps*span;

エラーレートカウンター System object™ を作成します。ReceiveDelay プロパティを設定して整合フィルターによる遅延が考慮されるようにします。

errorRate = comm.ErrorRate(ReceiveDelay=filtDelay);

バイナリデータを生成します。

x = randi([0 1],n,1);

データを変調します。

modSig = qammod(x,M,InputType="bit");

変調された信号をフィルター処理し、先頭から 1000 個のサンプルのアイダイアグラムをプロットします。

txSig = txfilter(modSig);
eyediagram(txSig(1:1000),sps)

Figure Eye Diagram contains 2 axes objects. Axes object 1 with title Eye Diagram for In-Phase Signal, xlabel Time, ylabel Amplitude contains an object of type line. This object represents In-phase. Axes object 2 with title Eye Diagram for Quadrature Signal, xlabel Time, ylabel Amplitude contains an object of type line. This object represents Quadrature.

$E_{b} / N_{0}$ を指定して S/N 比 (SNR) を dB 単位で計算します。関数 awgn を使用して AWGN チャネル経由で送信信号を渡します。

SNR = convertSNR(EbNo,"ebno","snr", ...
    SamplesPerSymbol=sps, ...
    BitsPerSymbol=bps);
noisySig = awgn(txSig,SNR,"measured");

ノイズを含む信号をフィルター処理し、アイダイアグラムと散布図を表示します。

rxSig = rxfilter(noisySig);
eyediagram(rxSig(1:1000),sps)

scatterplot(rxSig)

Figure Scatter Plot contains an axes object. The axes object with title Scatter plot, xlabel In-Phase, ylabel Quadrature contains a line object which displays its values using only markers. This object represents Channel 1.

フィルター処理された信号を復調し、誤り統計を計算します。フィルターによる遅延は、errorRate の ReceiveDelay プロパティによって考慮されています。

z = qamdemod(rxSig,M,OutputType="bit");

errStat = errorRate(x,z);
fprintf('\nBER = %5.2e\nBit Errors = %d\nBits Transmitted = %d\n',...
    errStat)

BER = 1.15e-03
Bit Errors = 23
Bits Transmitted = 19960

nzmod = awgn(modSig,SNR,"measured");
demodsig = qamdemod(nzmod,M,OutputType="bit");
errorRate2 = comm.ErrorRate;
errStat2 = errorRate2(x,demodsig);
fprintf('\nBER = %5.2e\nBit Errors = %d\nBits Transmitted = %d\n',...
    errStat2)

BER = 5.86e-02
Bit Errors = 1172
Bits Transmitted = 20000

レイズドコサインフィルター処理を用いた ISI の低減

ライブスクリプトを開く

レイズドコサインフィルター処理を用いて、非線形増幅器に起因する符号間干渉 (ISI) を低減します。

変調次数のシミュレーション変数を初期化します。

M = 16; % Modulation order

ルートレイズドコサインフィルターオブジェクトを作成します。

txfilter = comm.RaisedCosineTransmitFilter;
rxfilter = comm.RaisedCosineReceiveFilter;

無記憶非線形性 System object™ を作成し、変調した信号に非線形動作を導入します。名前と値のペアを使用し、Method プロパティを Saleh model に設定してハイパワーアンプをエミュレートします。

hpa = comm.MemorylessNonlinearity('Method','Saleh model', ...
    'InputScaling',-10,'OutputScaling',0);

ランダムな整数を生成して 16-QAM 変調を行います。

x = randi([0 M-1],1000,1);
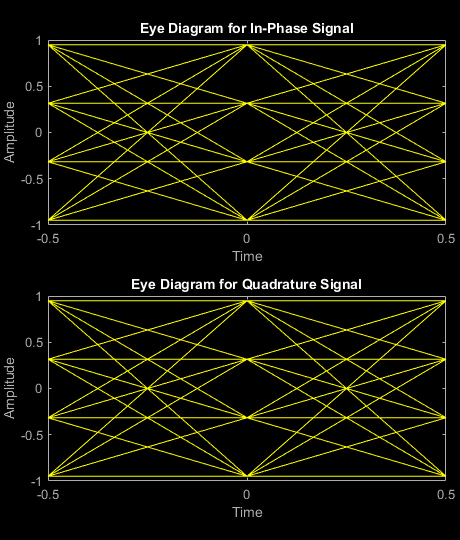
modSig = qammod(x,M,'UnitAveragePower',true);

変調した信号のアイダイアグラムをプロットします。時間 0 で、16-QAM 変調の明確な "目" が 3 つあります。

eyediagram(modSig,2)

hpa を使用して変調信号を増幅します。

txSigNoFilt = hpa(modSig);

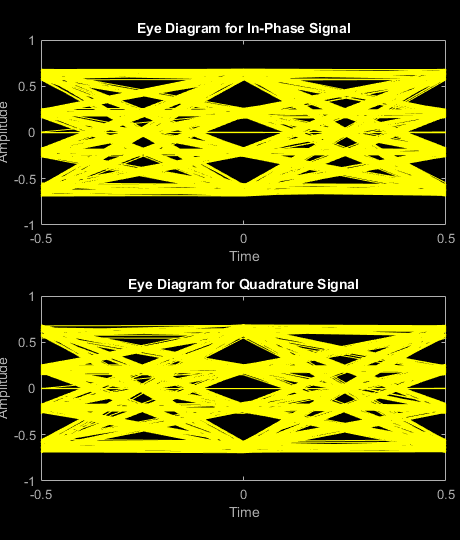
増幅した信号のアイダイアグラムを RRC フィルター処理なしでプロットします。時間 0 で複数の目があります。これは非線形増幅器からの符号間干渉の結果です。

eyediagram(txSigNoFilt,2)

RRC 送信フィルターを使用して、変調した信号をフィルター処理します。

filteredSig = txfilter(modSig);

hpa をリリースし、フィルター処理した信号を増幅します。フィルター内挿により入力信号次元が変化するため、関数 release が必要です。

release(hpa)
txSig = hpa(filteredSig);

RRC 整合受信フィルターを使用して txSig をフィルター処理します。

rxSig = rxfilter(txSig);

受信フィルターの適用後に信号のアイダイアグラムをプロットします。整合された RRC フィルターが ISI を緩和するため、再度 3 つの明確な目が現れます。

eyediagram(rxSig,2)

符号化およびフィルター処理した信号の遅延検出

ライブスクリプトを開く

畳み込み符号化とフィルター処理を行ったリンクの遅延を特定します。遅延を使用し、ビットエラーの数を計算しながら送信信号と受信信号を揃えます。

レイズドコサイン送信フィルターおよび受信フィルターの System object について、対応するペアを作成します。

txfilt = comm.RaisedCosineTransmitFilter;
rxfilt = comm.RaisedCosineReceiveFilter;

畳み込み符号化器とビタビ復号化器のペアを作成します。

convEnc = comm.ConvolutionalEncoder;
vitDec = comm.ViterbiDecoder(InputFormat='Hard');

ランダムなバイナリデータを生成します。データを畳み込み符号化します。

txData = randi([0 1],1000,1);
encData = convEnc(txData);

符号化したデータを変調します。レイズドコサイン送信フィルターを使用して変調されたデータを渡します。

modSig = pskmod(encData,4,InputType='bit');
txSig = txfilt(modSig);

フィルター処理された信号を AWGN チャネルを通して渡します。

rxSig = awgn(txSig,20,'measured');

受信信号をフィルター処理してから復調します。

filtSig = rxfilt(rxSig);
demodSig = pskdemod(filtSig,4,OutputType='bit');

復調したデータを復号化します。

rxData = vitDec(demodSig);

関数 finddelay を使用して、送受信されたバイナリデータ間の遅延を検出します。

td = finddelay(txData,rxData)

td = 
44

予想される遅延は、整合フィルターの群遅延とビタビ復号化器のトレースバック長の和に等しくなります。計算した遅延が予想された遅延と一致することを確認します。

tdexpected = ( ...
    txfilt.FilterSpanInSymbols ...
    + rxfilt.FilterSpanInSymbols)/2 + ...
    vitDec.TracebackDepth;
isequal(td,tdexpected)

ans = logical
   1

ビットエラーの数を計算するには、送信シーケンスの最後の td ビットと受信シーケンスの最初の td ビットを破棄して、送信信号と受信信号を揃えます。

numErrors = biterr(txData(1:end-td),rxData(td+1:end))

numErrors = 
0

Simulink でのレイズドコサインフィルターの設計

この例では次を使用します。

モデルを開く

次の例は、送信機がルートレイズドコサインフィルターを使用してパルス整形を実行し、対応する受信機が整合フィルターとしてルートレイズドコサインフィルターを使用する典型的な設定を示しています。この例では、フィルター処理された受信信号からアイダイアグラムをプロットします。

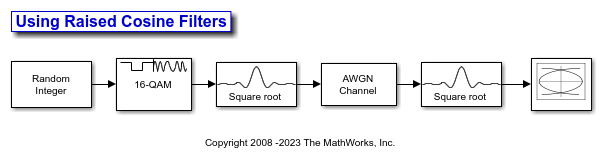
doc_rcfilters モデルは、16QAM 変調された信号に RRC フィルター処理を適用し、この信号に AWGN を付加し、アイダイアグラムを表示します。

Random Integer Generatorブロックは、[M-ary 数] を 16 に設定し、[サンプル時間] を 1/100 に設定します。また、[フレームあたりのサンプル数] を 100 に設定し、[フレームベースの出力] を選択します。
Rectangular QAM Modulator Basebandブロックは、[正規化方式] を Peak Power に設定し、[ピーク電力] を 1 に設定します。
Raised Cosine Transmit Filterブロックは、[Filter span in symbols] を 8 に設定し、[ロールオフ係数] を 0.2 に設定します。
AWGN チャネルブロックは、[モード] を Signal to noise ratio (SNR) に設定し、[SNR] を 40 に設定して、[入力信号パワー] を 0.0694 に設定します。ルートレイズドコサイン送信フィルターの電力ゲインは 1/N です。ここで、N はフィルターのアップサンプリング係数を表します。フィルターの入力信号強度は 0.5556 です。16-QAM 矩形変調器のピーク電力は 1 ワットに設定されているので、平均パワーは 0.5556 になります。したがって、フィルターの出力信号強度は (0.5556/8) = 0.0694 です。
Raised Cosine Receive Filterブロックは、[Filter span in symbols] を 8 に設定し、[ロールオフ係数] を 0.2 に設定します。
Eye Diagramブロックは、[トレースあたりのシンボル数] を 2 に設定し、[表示するトレース数] を 100 に設定します。

シミュレーションを実行するとアイダイアグラムが生成されます。この例では、大きい S/N 比により、アイ開口率が大きいアイダイアグラムが生成されます。AWGN Channel ブロックで [SNR] パラメーターを減らすと、ダイアグラムの "目" はますます閉じます。このアイダイアグラムには大きく開いた "目" が 2 つあり、復調する前にフィルター処理した信号をサンプリングするための適切な瞬間を示しています。また、このアイダイアグラムは、受信波形のサンプリングの瞬間にシンボル間の干渉がないことを示しています。

MATLAB 関数を使用したレイズドコサインフィルターの設計

ライブスクリプトを開く

関数rcosdesignは、有限インパルス応答 (FIR) レイズドコサイン (RC) フィルターおよびルートレイズドコサイン (RRC) フィルターを設計します。関数は、出力として FIR 係数を返します。信号にフィルター処理を適用するには、rcosdesign によって返された係数と共に関数upfirdnを使用します。

ロールオフ 0.25、フィルタースパン 6 シンボル、オーバーサンプリング係数 2 のルートレイズドコサイン FIR フィルターを設計します。

sps = 2;
num = rcosdesign(0.25,6,sps);
num(1:6)

ans = 1×6

   -0.0265    0.0462    0.0375   -0.1205   -0.0454    0.4399

num(7:end)

ans = 1×7

    0.7558    0.4399   -0.0454   -0.1205    0.0375    0.0462   -0.0265

ここで、ベクトル num には、フィルターの係数が $z^{- 1}$ の昇べきの順で格納されます。

関数 upfirdn を使用して、rcosdesign により生成されるレイズドコサインフィルターを使用してデータをフィルター処理します。アイダイアグラムは、num がレイズドコサインフィルターであることを示して、不完全な目になります。

d = 2*randi([0 1],100,1)-1;
f = upfirdn(d,num,sps);
eyediagram(f(7:200),sps)

Figure Eye Diagram contains an axes object. The axes object with title Eye Diagram, xlabel Time, ylabel Amplitude contains an object of type line. This object represents In-phase.

RRC フィルターを使った内挿と間引き

ライブスクリプトを開く

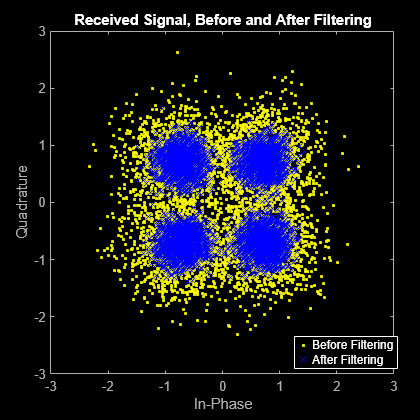
この例では、関数rcosdesignを使って設計されたルートレイズドコサインフィルターを使用して、信号を内挿および間引きする方法を説明します。

ルートレイズドコサインフィルターパラメーターを定義します。信号コンスタレーションパラメーターを定義します。

rolloff = 0.25; % Filter rolloff
span = 6;       % Filter span
sps = 4;        % Samples per symbol
M = 4;          % Size of the signal constellation
k = log2(M);    % Number of bits per symbol

関数 rcosdesign を使用してルートレイズドコサインフィルターの係数を生成します。

rrcFilter = rcosdesign(rolloff,span,sps);

関数 randi を使用して 10000 個のデータシンボルを生成します。

data = randi([0 M-1],10000,1);

データシンボルに PSK 変調を適用します。コンスタレーションサイズは 4 のため、変調タイプは QPSK です。

modData = pskmod(data,M,pi/4);

関数upfirdnを使用して、入力データをアップサンプリングし、フィルター処理します。

txSig = upfirdn(modData,rrcFilter,sps);

Eb/N0 を SNR に変換し、その後、この信号を AWGN チャネルを介して渡します。

EbNo = 7;
snr = convertSNR(EbNo,'ebno','snr', ...
    SamplesPerSymbol=sps, ...
    BitsPerSymbol=k);
rxSig = awgn(txSig,snr,'measured');

受信信号をフィルター処理し、ダウンサンプリングします。フィルター遅延を考慮して、信号の一部を削除します。

rxFilt = upfirdn(rxSig,rrcFilter,1,sps);
rxFilt = rxFilt(span+1:end-span);

最初の 5000 個のシンボルを使用して、変調したデータのscatterplotを作成します。

hScatter = scatterplot(sqrt(sps)* ...
    rxSig(1:sps*5000), ...
    sps,0);
hold on
scatterplot(rxFilt(1:5000),1,0,'bx',hScatter)
title('Received Signal, Before and After Filtering')
legend('Before Filtering','After Filtering')
axis([-3 3 -3 3]) % Set axis ranges
hold off

Figure Scatter Plot contains an axes object. The axes object with title Received Signal, Before and After Filtering, xlabel In-Phase, ylabel Quadrature contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Before Filtering, After Filtering.

参照

[1] Korn, Israel, Digital Communications, New York, Van Nostrand Reinhold, 1985.

[2] Oppenheim, Alan V., and Ronald W. Schafer, Discrete-Time Signal Processing, Englewood Cliffs, NJ, Prentice Hall, 1989.

[3] Proakis, John G. Digital Communications. 5th ed. New York: McGraw Hill, 2007.

[4] Rappaport, Theodore S. Wireless Communications: Principles and Practice. Upper Saddle River, NJ: Prentice Hall, 1996.

[5] Sklar, Bernard. Digital Communications: Fundamentals and Applications. Englewood Cliffs, NJ: Prentice-Hall, 1988.