群遅延

フィルターの "群遅延" では、フィルターの平均の時間遅延を周波数の関数として表します。フィルターの複素周波数応答 H(ejω) の場合、群遅延は、フィルターの位相応答の負の 1 次導関数として定義されます。

−ddωθ(ω)

ここで、θ はフィルターの位相、ω はラジアン/秒単位の周波数を表します。線形位相有限インパルス応答 (FIR) フィルターの場合、群遅延はフィルターの次数 (スパン) の 1/2 になります。このフィルターのインパルス応答の長さは (L×N + 1) です。ここで、N はシンボル内のフィルター スパン、L はシンボルあたりのサンプル数です。これにより、時刻 0 より前のインパルス応答のエネルギーが無視できるほどの量となるように遅延が設定され、フィルターの初期応答とピーク応答の間の時間が測定されます。

インパルスのピークと群遅延の相関

ライブ スクリプトを開く

次の図に示すルート レイズド コサイン (RRC) フィルターのインパルス応答は、8 シンボルのフィルター スパンを使用しています。インパルス応答のピークは 4 番目のシンボルで発生しており、群遅延に対応しています。

rf = 0.25; % Rolloff factor
span = 8;  % Span of filter 
sps = 20;  % Samples per symbol

h1 = rcosdesign(rf,span,sps,"sqrt");
x = [0:length(h1)-1]/sps;
plot(x,h1)

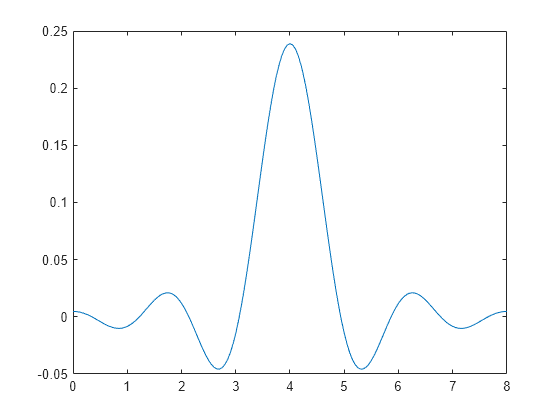
Figure contains an axes object. The axes object contains an object of type line.

関数grpdelayを使用して、フィルターの群遅延を計算します。結果をシンボルに変換し、それがフィルターのピークの位置に一致することを確認します。

gd = grpdelay(h1);
groupDelayInSymbols = gd(1)/sps
groupDelayInSymbols = 
4

シミュレーションでの遅延の影響

信号をフィルター処理した結果として生じる群遅延は、シミュレーションの他の部分に影響します。たとえば、次の図で Symbols In および Symbols Out とマークされたシンボル ストリームをエラー レートのプロットまたは計算によって比較するとします。群遅延の合計と等しくなるように遅延を設定します。モデルでルート レイズド コサイン フィルターのペアを使用する場合は、両方の群遅延を合計します。次のようにして、入力シンボルと出力シンボルの間の遅延の合計を求めます。

  • MATLAB® の場合は関数 finddelay を使用します。

  • Simulink® の場合は Find Delay ブロックを使用します。

正確に対応しているシンボルを比較するには、次の方法のいずれかを使用してください。

  • 次の図に示すように、システム コンポーネントのパスと並列のパスに遅延を挿入することで、Symbols In 信号と Symbols Out 信号を整列させることができます。

    Communications link showing error rate calculation comparing input and output symbols. A delay is added to input symbols to align with symbols output after transmit RRC filter, channel, and receive RRC filter processing.

    • MATLAB の場合は関数 alignsignals を使用します。

    • Simulink の場合は Delay ブロックを使用します。

  • または、MATLAB では comm.ErrorRate System object™、Simulink では Error Rate Calculation ブロックを使用した場合、送信側の Symbols In 入力と受信側の Symbols Out についてそれぞれ受信遅延と計算遅延のプロパティおよびパラメーターを設定することで、これらの信号を整列させることができます。

モデルの遅延を管理する方法の詳細については、遅延とレイテンシを参照してください。

参考

関数

オブジェクト

ブロック

トピック