grpdelay

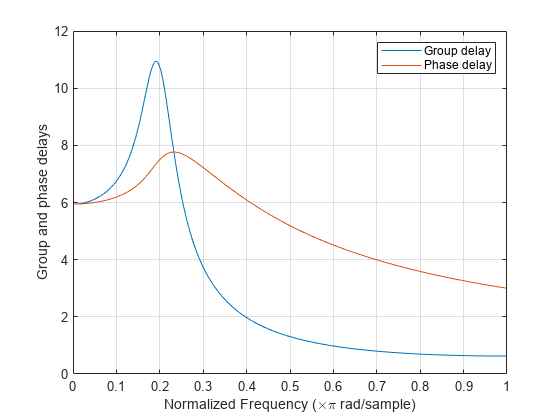
平均フィルター遅延 (群遅延)

構文

[gd,w] = grpdelay(b,a,n)

[gd,w] = grpdelay(B,A,"ctf",n)

[gd,w] = grpdelay({B,A,g},"ctf",n)

[gd,w] = grpdelay(d,n)

[gd,w] = grpdelay(sos,n)

[gd,w] = grpdelay(___,"whole")

[gd,f] = grpdelay(___,n,fs)

[gd,f] = grpdelay(___,n,"whole",fs)

gd = grpdelay(___,win)

gd = grpdelay(___,fin,fs)

grpdelay(___)

説明

[gd,w] = grpdelay(b,a,n) は、指定されたデジタル フィルターの群遅延応答を返します。分子係数 b と分母係数 a をもつデジタル フィルターを指定します。この関数は、n 点群遅延応答ベクトルを gd で返し、対応する角周波数ベクトルを w で返します。

[gd,w] = grpdelay(B,A,"ctf",n) は、分子係数 B と分母係数 A をもつCascaded Transfer Functions (CTF) として表されるデジタル フィルターの n 点群遅延応答を返します。 (R2024b 以降)

[gd,w] = grpdelay({B,A,g},"ctf",n) は、デジタル フィルターの n 点群遅延応答を CTF 形式で返します。分子係数 B、分母係数 A、およびフィルター セクション全体のスケーリング値 g を使用してフィルターを指定します。 (R2024b 以降)

[gd,w] = grpdelay(d,n) では、デジタル フィルター d の n 点の群遅延応答が返されます。

[gd,w] = grpdelay(sos,n) では、2 次セクション行列 sos に対応する n 点の群遅延応答が返されます。

[gd,w] = grpdelay(___,"whole") では、単位円全体で n 個のサンプル点の群遅延が返されます。

[gd,f] = grpdelay(___,n,fs) では、レート fs でサンプリングされたフィルター信号に設計されたデジタル フィルターに対し、群遅延応答ベクトル gd とそれに対応する物理周波数ベクトル f が返されます。

[gd,f] = grpdelay(___,n,"whole",fs) では、0 から fs の範囲の n 個の点における周波数ベクトルが返されます。

gd = grpdelay(___,win) では、win で提供される正規化周波数で評価された群遅延応答ベクトル gd が返されます。

gd = grpdelay(___,fin,fs) では、fin で提供される物理周波数で評価された群遅延応答ベクトル gd が返されます。

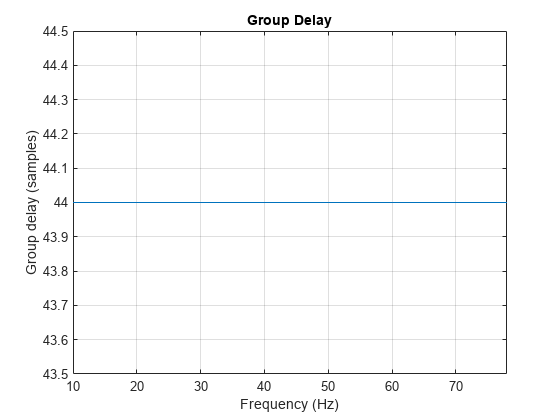
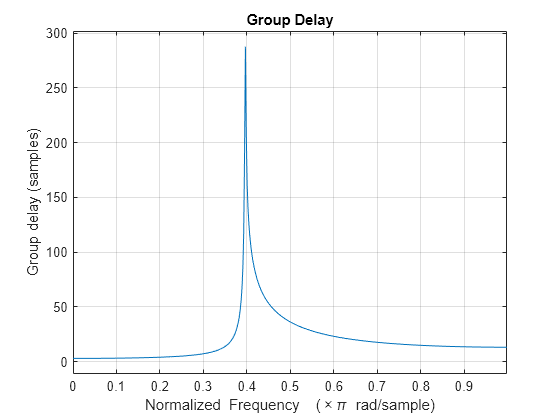
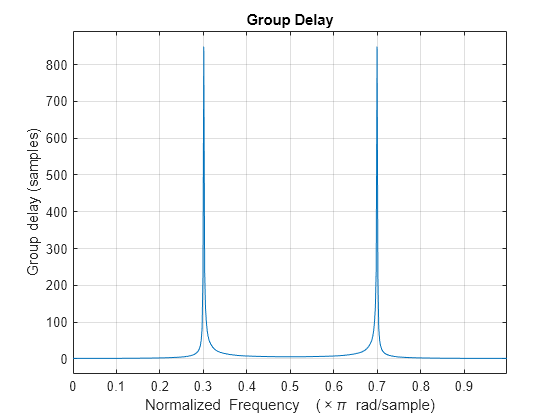
出力引数なしで grpdelay(___) を使用すると、フィルターの群遅延応答がプロットされます。

例

バタワース フィルターの群遅延

正規化された 3 dB の周波数 $$0.2\pi$$ ラジアン/サンプルをもつ次数 6 のバタワース フィルターを設計します。grpdelay を使用して群遅延を表示します。

[z,p,k] = butter(6,0.2);
sos = zp2sos(z,p,k);

grpdelay(sos,128)

同じ Figure 内で、システムの群遅延と位相遅延をプロットします。

gd = grpdelay(sos,512);

[h,w] = freqz(sos,512);
pd = -unwrap(angle(h))./w;

plot(w/pi,gd,w/pi,pd)
grid
xlabel 'Normalized Frequency (\times\pi rad/sample)'
ylabel 'Group and phase delays'
legend('Group delay','Phase delay')

バタワース digitalFilter の群遅延応答

designfilt を使用して、正規化された 3 dB の周波数 $$0.2\pi$$ ラジアン/サンプルをもつ 6 次のバタワース フィルターを設計します。その群遅延応答を表示します。

d = designfilt("lowpassiir",FilterOrder=6, ...
    HalfPowerFrequency=0.2,DesignMethod="butter");
grpdelay(d)

任意振幅応答 FIR フィルターの群遅延応答

任意振幅応答の 88 次 FIR フィルターを設計します。フィルターには、2 つの通過帯域と 2 つの阻止帯域があります。低域周波数の通過帯域は、高周波数の通過帯域のゲインの 2 倍です。サンプル レート 200 Hz を指定します。10 Hz から 78 Hz までのフィルターの振幅応答と位相応答を可視化します。

fs = 200;
d = designfilt('arbmagfir', ...
       'FilterOrder',88, ...
       'NumBands',4, ...
       'BandFrequencies1',[0 20], ...
       'BandFrequencies2',[25 40], ...
       'BandFrequencies3',[45 65], ...
       'BandFrequencies4',[70 100], ...
       'BandAmplitudes1',[2 2], ...
       'BandAmplitudes2',[0 0], ...
       'BandAmplitudes3',[1 1], ...
       'BandAmplitudes4',[0 0], ...
       'SampleRate',fs);
freqz(d,10:1/fs:78,fs)

同じ周波数範囲上のフィルターの群遅延応答を計算して表示します。フィルター次数の 1/2 であることを確認します。

filtord(d)

ans = 
88

grpdelay(d,10:1/fs:78,fs)

カスケード伝達関数の群遅延応答

R2024b 以降

阻止帯域エッジ周波数が 0.4、阻止帯域の減衰量が 50 dB の 40 次ローパス チェビシェフ II 型デジタル フィルターを設計します。CTF 形式の係数を使用して、フィルターの群遅延応答をプロットします。

[B,A] = cheby2(40,50,0.4,"ctf");

grpdelay(B,A,"ctf")

通過帯域エッジ周波数が 0.3 と 0.7、通過帯域リップルが 0.1 dB、阻止帯域の減衰量が 50 dB の 30 次バンドパス楕円デジタル フィルターを設計します。CTF 形式の係数とゲインを使用して、フィルターの群遅延応答をプロットします。

[B,A,g] = ellip(30,0.1,50,[0.3 0.7],"ctf");
grpdelay({B,A,g},"ctf")

入力引数

b, a — 伝達関数の係数

ベクトル

伝達関数の係数。ベクトルで指定します。b と a によるこの伝達関数式は次になります。

$$H(z)=\frac{B(z)}{A(z)}=\frac{b_1+b_2{z}^{-1}\cdots +b_n{z}^{-\left(n-1\right)}+b_{n+1}{z}^{-n}}{a_1+a_2{z}^{-1}\cdots +a_m{z}^{-\left(m-1\right)}+a_{m+1}{z}^{-m}}$$

例: b = [1 3 3 1]/6 と a = [3 0 1 0]/3 は、正規化された 3 dB の周波数 0.5π ラジアン/サンプルをもつ 3 次のバタワース フィルターを指定します。

データ型: double | single
複素数のサポート: あり

n — 応答を求める周波数点の数

512 (既定値) | 正の整数スカラー

応答を求める周波数点の数。2 以上の正の整数スカラーとして指定します。n がない場合の既定値は 512 です。最適な結果を得るため、n をフィルター次数よりも大きい値に設定します。

B,A — カスケード伝達関数 (CTF) 係数

スカラー | ベクトル | 行列

R2024b 以降

カスケード伝達関数 (CTF) 係数。スカラー、ベクトル、または行列として指定します。B と A は、それぞれカスケード伝達関数の分子係数と分母係数をリストします。

B のサイズは L 行 (m + 1) 列、A のサイズは L 行 (n + 1) でなければなりません。ここで、

• L はフィルター セクションの数を表します。

• m はフィルターの分子の次数を表します。

• n はフィルターの分母の次数を表します。

カスケード伝達関数の形式と係数行列の詳細については、CTF 形式によるデジタル フィルターの指定を参照してください。

メモ

A(:,1) のいずれかの要素が 1 と等しくない場合、grpdelay はフィルター係数を A(:,1) で正規化します。この場合、A(:,1) はゼロ以外でなければなりません。

データ型: double | single
複素数のサポート: あり

g — スケール値

スカラー | ベクトル

R2024b 以降

スケール値。実数値のスカラー、または L + 1 個の要素をもつ実数値のベクトルとして指定します。ここで、L は CTF セクションの数です。スケール値は、カスケード フィルター表現のセクション全体にわたるフィルター ゲインの分布を表します。

grpdelay 関数は、g の指定方法に応じて、scaleFilterSections 関数を使用してフィルター セクションにゲインを適用します。

• スカラー — この関数は、すべてのフィルター セクションにわたってゲインを均一に配分します。

• ベクトル — この関数は、最初の L 個のゲイン値を対応するフィルター セクションに適用し、最後のゲイン値をすべてのフィルター セクションに均一に配分します。

データ型: double | single

d — デジタル フィルター

digitalFilter オブジェクト

デジタル フィルター。digitalFilter オブジェクトで指定します。デジタル フィルターを周波数応答仕様に基づいて生成するには、関数 designfilt を使用します。

例: d = designfilt('lowpassiir','FilterOrder',3,'HalfPowerFrequency',0.5) は、正規化された 3 dB の周波数 0.5π ラジアン/サンプルをもつ 3 次のバタワース フィルターを指定します。

sos — 2 次セクションの係数

行列

2 次セクションの係数。行列として指定します。sos は K 行 6 列の行列で、セクション数 K が 2 以上でなければなりません。セクション数が 2 未満の場合、関数は入力を分子ベクトルとして扱います。sos の各行は 2 次 (双二次) フィルターの係数に対応しています。sos の i 行目は [bi(1) bi(2) bi(3) ai(1) ai(2) ai(3)] に対応しています。

例: s = [2 4 2 6 0 2;3 3 0 6 0 0] は、正規化された 3 dB の周波数 0.5π ラジアン/サンプルをもつ 3 次のバタワース フィルターを指定します。

データ型: double | single
複素数のサポート: あり

fs — サンプル レート

正のスカラー

サンプル レート。正のスカラーで指定します。時間の単位が秒の場合、fs は Hz で表されます。

データ型: double

win — 角周波数

ベクトル

角周波数。ラジアン/サンプル単位のベクトルとして指定します。win は少なくとも 2 つの要素をもたなければなりません。そうでない場合は関数が n として解釈するためです。win = π はナイキスト周波数に相当します。

fin — 周波数

ベクトル

周波数。ベクトルとして指定します。fin は少なくとも 2 つの要素をもたなければなりません。そうでない場合は、関数が n として解釈するためです。時間の単位が秒の場合、fin は Hz で表されます。

データ型: double

出力引数

gd — 群遅延応答

ベクトル

群遅延応答。ベクトルとして返されます。n を指定している場合は、gd の長さは n になります。n を指定していないか、n を空ベクトルとして指定している場合には、gd の長さは 512 になります。

grpdelay への入力が単精度の場合、関数によって、群遅延が単精度演算で計算されます。出力 h は単精度です。

w — 角周波数

ベクトル

ベクトルとして返される角周波数。w は 0 ～π の値を取ります。入力に "whole" を指定すると、w の値の範囲は 0 ～ 2π になります。n を指定している場合は、w の長さは n になります。n を指定していないか、n を空ベクトルとして指定している場合には、w の長さは 512 になります。

f — 周波数

ベクトル

Hz 表記のベクトルとして返される周波数。f は 0 ～ fs/2 Hz の値を取ります。入力に "whole" を指定している場合、f の値の範囲は 0 ～ fs Hz になります。n を指定している場合は、f の長さは n になります。n を指定していないか、n を空ベクトルとして指定している場合には、f の長さは 512 になります。

詳細

群遅延

フィルターの "群遅延応答" とは、フィルターの平均の遅延を周波数の関数として表したものです。これは、フィルターの位相応答の 1 次導関数に負の符号を付けたものです。フィルターの周波数応答が H(e^jω) の場合、群遅延は以下になります。

$${\tau }_g(\omega )=-\frac{d\theta (\omega )}{d\omega },$$

ここで、θ(ω) は位相、つまり H(e^jω) の引数です。

カスケード伝達関数

IIR デジタル フィルターをカスケード セクションに分割すると、数値安定性が向上し、係数の量子化誤差の影響を受けにくくなります。L 個の伝達関数 H₁(z)、H₂(z)、…、H_L(z) による伝達関数 H(z) のカスケード形式は次のとおりです。

$$H(z)={\displaystyle \prod _{l=1}^L{H}_l(z)}=H_1(z)\times H_2(z)\times \cdots \times H_L(z).$$

CTF 形式によるデジタル フィルターの指定

解析、可視化、信号フィルター処理で使用するため、CTF 形式でデジタル フィルターを指定できます。係数 B と A をリストしてフィルターを指定します。スカラーまたはベクトルの g を指定することで、セクション全体にフィルターのスケーリング ゲインを含めることもできます。

フィルター係数

係数を L 行の行列

$$B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1,m+1}\\ b_{21}& b_{22}& \cdots & b_{2,m+1}\\ ⋮& ⋮& \ddots & ⋮\\ b_{L1}& b_{L2}& \cdots & b_{L,m+1}\end{array}\right],A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1,n+1}\\ a_{21}& a_{22}& \cdots & a_{2,n+1}\\ ⋮& ⋮& \ddots & ⋮\\ a_{L1}& a_{L2}& \cdots & a_{L,n+1}\end{array}\right],$$

として指定した場合、L 個のカスケード伝達関数のシーケンスとしてフィルターを指定したものとみなされます。このとき、フィルターの完全な伝達関数は次のようになります。

$$H\left(z\right)=\frac{b_{11}+b_{12}{z}^{-1}+\cdots +b_{1,m+1}{z}^{-m}}{a_{11}+a_{12}{z}^{-1}+\cdots +a_{1,n+1}{z}^{-n}}\times \frac{b_{21}+b_{22}{z}^{-1}+\cdots +b_{2,m+1}{z}^{-m}}{a_{21}+a_{22}{z}^{-1}+\cdots +a_{2,n+1}{z}^{-n}}\times \cdots \times \frac{b_{L1}+b_{L2}{z}^{-1}+\cdots +b_{L,m+1}{z}^{-m}}{a_{L1}+a_{L2}{z}^{-1}+\cdots +a_{L,n+1}{z}^{-n}},$$

ここで、m ≥ 0 はフィルターの "分子次数"、n ≥ 0 は "分母次数" です。

• B と A の両方をベクトルとして指定した場合、基になるシステムは 1 つのセクションから成る IIR フィルター (L = 1) であるとみなされます。このとき、B は伝達関数の分子を表し、A はその分母を表します。

• B がスカラーの場合、フィルターは全極 IIR フィルターのカスケードであるとみなされます。このとき、各セクションの全体的なシステム ゲインは B に等しくなります。

• A がスカラーの場合、フィルターは FIR フィルターのカスケードであるとみなされます。このとき、各セクションの全体的なシステム ゲインは 1/A に等しくなります。

メモ

• 2 次セクションの行列をカスケード伝達関数に変換するには、sos2ctf 関数を使用します。

• 零点-極-ゲイン フィルター表現をカスケード伝達関数に変換するには、zp2ctf 関数を使用します。

係数とゲイン

全体的なスケーリング ゲイン、または係数値から共通因数としてくくりだされた複数のスケーリング ゲインがある場合、係数とゲインを {B,A,g} 形式の cell 配列として指定できます。フィルター セクションのスケーリングは、固定小数点演算を使用して各フィルター セクションの出力の振幅レベルを確実に同等にする場合に特に重要であり、数値精度の制限によるフィルター応答の不正確さを回避するのに役立ちます。

ゲインは、全体的なゲインを表すスカラー、またはセクションのゲインを表すベクトルとして指定できます。

• ゲインがスカラーの場合、その値はすべてのカスケード フィルター セクションに均一に適用されます。

• ゲインがベクトルの場合、カスケード内のフィルター セクションの数 L よりも 1 つ多い要素をもたなければなりません。最初の L 個のスケール値はそれぞれ対応するフィルター セクションに適用され、最後の値はすべてのカスケード フィルター セクションに均一に適用されます。

係数行列とゲイン ベクトルを

$$B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1,m+1}\\ b_{21}& b_{22}& \cdots & b_{2,m+1}\\ ⋮& ⋮& \ddots & ⋮\\ b_{L1}& b_{L2}& \cdots & b_{L,m+1}\end{array}\right],A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1,n+1}\\ a_{21}& a_{22}& \cdots & a_{2,n+1}\\ ⋮& ⋮& \ddots & ⋮\\ a_{L1}& a_{L2}& \cdots & a_{L,n+1}\end{array}\right],g=\left[\begin{array}{ccccc}{g}_1& g_2& \cdots & g_L& g_{\text{S}}\end{array}\right],$$

として指定した場合、フィルター システムの伝達関数は次であるとみなされます。

$$H\left(z\right)=g_{\text{S}}\left(g_1\frac{b_{11}+b_{12}{z}^{-1}+\cdots +b_{1,m+1}{z}^{-m}}{a_{11}+a_{12}{z}^{-1}+\cdots +a_{1,n+1}{z}^{-n}}\times g_2\frac{b_{21}+b_{22}{z}^{-1}+\cdots +b_{2,m+1}{z}^{-m}}{a_{21}+a_{22}{z}^{-1}+\cdots +a_{2,n+1}{z}^{-n}}\times \cdots \times g_L\frac{b_{L1}+b_{L2}{z}^{-1}+\cdots +b_{L,m+1}{z}^{-m}}{a_{L1}+a_{L2}{z}^{-1}+\cdots +a_{L,n+1}{z}^{-n}}\right).$$

ヒント

• スケーリング ゲインを含むフィルターを CTF 形式で取得できます。butter、cheby1、cheby2、ellip などのデジタル IIR フィルター設計関数の出力を使用します。これらの関数で、"ctf" フィルタータイプ引数を指定し、スケール値を取得するために B、A、g を返すように指定します。 (R2024b 以降)

参照

[1] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• grpdelay 関数に CTF 係数を入力する場合、コードを生成するには、grpdelay 構文に "ctf" 入力引数を含めなければなりません。

バージョン履歴

R2006a より前に導入

R2025a: [プロットの作成] ライブ エディター タスクを使用したカスケード伝達関数の可視化

[プロットの作成] ライブ エディター タスクでカスケード伝達関数 (CTF) を使用して、grpdelay の出力を対話的に可視化できます。

R2024b: カスケード伝達関数を使用したフィルターの解析

grpdelay 関数は、カスケード伝達関数 (CTF) 形式の入力をサポートします。

R2023a: [プロットの作成] ライブ エディター タスクを使用した関数出力の可視化

[プロットの作成] ライブ エディター タスクを使用して、grpdelay の出力を対話的に可視化することができるようになりました。さまざまなグラフ タイプを選択し、オプションのパラメーターを設定できます。タスクは、ライブ スクリプトの一部となるコードも自動的に生成します。

参考

アプリ

• フィルター アナライザー | フィルター デザイナー

関数

• ctffilt | cceps | designfilt | digitalFilter | fft | freqz | hilbert | icceps | phasedelay | rceps

Teaching Resources

• Digital Signal Processing: Signals and Filter Design (MathWorks Teaching Resources)