solve
最適化問題または方程式問題の求解
構文
説明
solve を使用して、最適化問題または方程式問題の解を求めます。
ヒント
完全なワークフローについては、問題ベースの最適化ワークフローまたは方程式を解くための問題ベースのワークフローを参照してください。
sol = solve(___,Name,Value)
例
線形計画問題を解く
最適化問題によって定義された線形計画問題を解きます。
x = optimvar('x'); y = optimvar('y'); prob = optimproblem; prob.Objective = -x - y/3; prob.Constraints.cons1 = x + y <= 2; prob.Constraints.cons2 = x + y/4 <= 1; prob.Constraints.cons3 = x - y <= 2; prob.Constraints.cons4 = x/4 + y >= -1; prob.Constraints.cons5 = x + y >= 1; prob.Constraints.cons6 = -x + y <= 2; sol = solve(prob)
Solving problem using linprog. Optimal solution found.
sol = struct with fields:
x: 0.6667
y: 1.3333
問題ベースのアプローチを使用した非線形計画問題の解法
MATLAB® に含まれる関数 peaks の、領域 での最小値を求めます。これを行うために、最適化変数の x と y を作成します。
x = optimvar('x'); y = optimvar('y');
peaks を目的関数とする最適化問題を作成します。
prob = optimproblem("Objective",peaks(x,y));制約を不等式として最適化変数に含めます。
prob.Constraints = x^2 + y^2 <= 4;
x の初期点を 1、y を –1 に設定し、問題を解きます。
x0.x = 1; x0.y = -1; sol = solve(prob,x0)
Solving problem using fmincon. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance.
sol = struct with fields:
x: 0.2283
y: -1.6255
fcn2optimexpr を必要とするサポートされていない関数
目的関数または非線形制約関数が初等関数で構成されていない場合は、fcn2optimexprを使用して、その関数を最適化式に変換しなければなりません。詳細については、非線形関数から最適化式への変換と最適化変数および式でサポートされる演算を参照してください。
現在の例を変換するには:
convpeaks = fcn2optimexpr(@peaks,x,y); prob.Objective = convpeaks; sol2 = solve(prob,x0)
Solving problem using fmincon. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance.
sol2 = struct with fields:
x: 0.2283
y: -1.6255
Copyright 2018–2020 The MathWorks, Inc.
初期点から始める混合整数線形計画法の解法
初期実行可能点がある場合とない場合の両方について整数計画問題を解くためのステップ数を比較します。問題には 8 つの整数変数と 4 つの線形等式制約があり、すべての変数が正になるように制限されています。
prob = optimproblem; x = optimvar('x',8,1,'LowerBound',0,'Type','integer');
4 つの線形等式制約を作成し、問題に含めます。
Aeq = [22 13 26 33 21 3 14 26
39 16 22 28 26 30 23 24
18 14 29 27 30 38 26 26
41 26 28 36 18 38 16 26];
beq = [ 7872
10466
11322
12058];
cons = Aeq*x == beq;
prob.Constraints.cons = cons;目的関数を作成し、問題に含めます。
f = [2 10 13 17 7 5 7 3]; prob.Objective = f*x;
初期点を使用せずに問題を解き、表示を調べて分枝限定ノードの数を確認します。
[x1,fval1,exitflag1,output1] = solve(prob);
Solving problem using intlinprog.
LP: Optimal objective value is 1554.047531.
Cut Generation: Applied 8 strong CG cuts.
Lower bound is 1591.000000.
Branch and Bound:
nodes total num int integer relative
explored time (s) solution fval gap (%)
10000 0.44 0 - -
14739 0.61 1 2.154000e+03 2.593968e+01
18258 0.76 2 1.854000e+03 1.180593e+01
18673 0.78 2 1.854000e+03 1.563342e+00
18829 0.78 2 1.854000e+03 0.000000e+00
Optimal solution found.
Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0. The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05.
比較するため、初期実行可能点を使用して解を求めます。
x0.x = [8 62 23 103 53 84 46 34]'; [x2,fval2,exitflag2,output2] = solve(prob,x0);
Solving problem using intlinprog.
LP: Optimal objective value is 1554.047531.
Cut Generation: Applied 8 strong CG cuts.
Lower bound is 1591.000000.
Relative gap is 59.20%.
Branch and Bound:
nodes total num int integer relative
explored time (s) solution fval gap (%)
3627 0.21 2 2.154000e+03 2.593968e+01
5844 0.30 3 1.854000e+03 1.180593e+01
6204 0.32 3 1.854000e+03 1.455526e+00
6400 0.33 3 1.854000e+03 0.000000e+00
Optimal solution found.
Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0. The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05.
fprintf('Without an initial point, solve took %d steps.\nWith an initial point, solve took %d steps.',output1.numnodes,output2.numnodes)Without an initial point, solve took 18829 steps. With an initial point, solve took 6400 steps.
初期点を与えることが常に問題を改善するとは限りません。この問題の場合、初期点を使用すると、時間と計算ステップが節減されます。ただし、問題によっては、初期点によって solve がより多くのステップを必要とする場合があります。
surrogateopt の開始点と値の指定 (問題ベース)
一部のソルバーでは、目的関数値と制約関数値がある場合、それらの値を x0 引数の solve に渡すことができます。これによってソルバーの時間を短縮できます。OptimizationValues オブジェクトのベクトルを渡します。関数 optimvalues を使用して、これらのベクトルを作成します。
目的関数値を使用できるソルバーは次のとおりです。
gagamultiobjparetosearchsurrogateopt
非線形制約関数値を使用できるソルバーは次のとおりです。
paretosearchsurrogateopt
たとえば、初期点のグリッドからの値で開始し、surrogateopt を使用して関数 peaks を最小化します。変数 x に -10 ～ 10 のグリッドを作成し、変数 y に間隔 1/2 で –5/2 ～ 5/2 のグリッドを作成します。初期点での目的関数値を計算します。
x = optimvar("x",LowerBound=-10,UpperBound=10); y = optimvar("y",LowerBound=-5/2,UpperBound=5/2); prob = optimproblem("Objective",peaks(x,y)); xval = -10:10; yval = (-5:5)/2; [x0x,x0y] = meshgrid(xval,yval); peaksvals = peaks(x0x,x0y);
optimvalues を使用して x0 引数の値を渡します。これにより、solve が値を計算する必要がなくなり、solve の時間が短縮されます。行ベクトルとして値を渡します。
x0 = optimvalues(prob,'x',x0x(:)','y',x0y(:)',... "Objective",peaksvals(:)');
surrogateopt と初期値を使用して、問題を解きます。
[sol,fval,eflag,output] = solve(prob,x0,Solver="surrogateopt")Solving problem using surrogateopt.
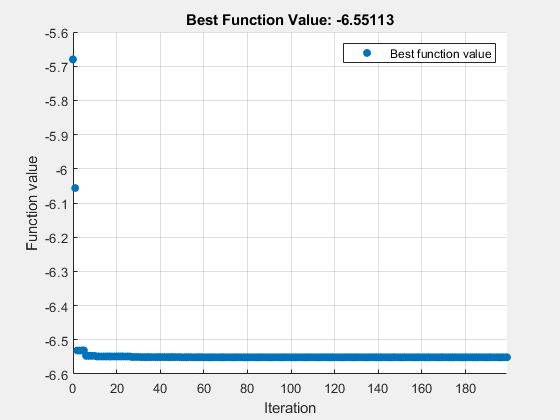
surrogateopt stopped because it exceeded the function evaluation limit set by 'options.MaxFunctionEvaluations'.
sol = struct with fields:
x: 0.2283
y: -1.6256
fval = -6.5511
eflag =
SolverLimitExceeded
output = struct with fields:
elapsedtime: 44.3507
funccount: 200
constrviolation: 0
ineq: [1x1 struct]
rngstate: [1x1 struct]
message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ...'
solver: 'surrogateopt'
複数開始点ソルバーを使用した非線形関数の最小化 (問題ベース)
点 [–1,2] から開始して、範囲 で関数 peaks の局所的最小値を求めます。
x = optimvar("x",LowerBound=-5,UpperBound=5); y = optimvar("y",LowerBound=-5,UpperBound=5); x0.x = -1; x0.y = 2; prob = optimproblem(Objective=peaks(x,y)); opts = optimoptions("fmincon",Display="none"); [sol,fval] = solve(prob,x0,Options=opts)
sol = struct with fields:
x: -3.3867
y: 3.6341
fval = 1.1224e-07
GlobalSearch ソルバーを使用して、より良い解を求めようとします。このソルバーは fmincon を複数回実行しますが、それによってより良い解が得られる可能性があります。
ms = GlobalSearch; [sol2,fval2] = solve(prob,x0,ms)
Solving problem using GlobalSearch. GlobalSearch stopped because it analyzed all the trial points. All 15 local solver runs converged with a positive local solver exit flag.
sol2 = struct with fields:
x: 0.2283
y: -1.6255
fval2 = -6.5511
GlobalSearch は、より良い (小さい) 目的関数値をもつ解を求めます。終了メッセージは、ローカル ソルバーの fmincon が 15 回実行されていることを示しています。返された解は、約 –6.5511 の目的関数値をもちます。この値は、最初の解における値である 1.1224e–07 より小さくなります。
既定ではないオプションによる整数計画問題を解く
問題を解く
反復表示を使用しません。
x = optimvar('x',2,1,'LowerBound',0); x3 = optimvar('x3','Type','integer','LowerBound',0,'UpperBound',1); prob = optimproblem; prob.Objective = -3*x(1) - 2*x(2) - x3; prob.Constraints.cons1 = x(1) + x(2) + x3 <= 7; prob.Constraints.cons2 = 4*x(1) + 2*x(2) + x3 == 12; options = optimoptions('intlinprog','Display','off'); sol = solve(prob,'Options',options)
sol = struct with fields:
x: [2x1 double]
x3: 1
解を検証します。
sol.x
ans = 2×1
0
5.5000
sol.x3
ans = 1
intlinprog を使用して線形計画法を解く
solve に線形計画問題のソルバーとして intlinprog を使用するように強制します。
x = optimvar('x'); y = optimvar('y'); prob = optimproblem; prob.Objective = -x - y/3; prob.Constraints.cons1 = x + y <= 2; prob.Constraints.cons2 = x + y/4 <= 1; prob.Constraints.cons3 = x - y <= 2; prob.Constraints.cons4 = x/4 + y >= -1; prob.Constraints.cons5 = x + y >= 1; prob.Constraints.cons6 = -x + y <= 2; sol = solve(prob,'Solver', 'intlinprog')
Solving problem using intlinprog. LP: Optimal objective value is -1.111111. Optimal solution found. No integer variables specified. Intlinprog solved the linear problem.
sol = struct with fields:
x: 0.6667
y: 1.3333
すべての出力を返す
既定ではないオプションによる整数計画問題を解くで説明されている混合整数線形計画問題を解いて、すべての出力データを検証します。
x = optimvar('x',2,1,'LowerBound',0); x3 = optimvar('x3','Type','integer','LowerBound',0,'UpperBound',1); prob = optimproblem; prob.Objective = -3*x(1) - 2*x(2) - x3; prob.Constraints.cons1 = x(1) + x(2) + x3 <= 7; prob.Constraints.cons2 = 4*x(1) + 2*x(2) + x3 == 12; [sol,fval,exitflag,output] = solve(prob)
Solving problem using intlinprog. LP: Optimal objective value is -12.000000. Optimal solution found. Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0. The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05.
sol = struct with fields:
x: [2x1 double]
x3: 1
fval = -12
exitflag =
OptimalSolution
output = struct with fields:
relativegap: 0
absolutegap: 0
numfeaspoints: 1
numnodes: 0
constrviolation: 0
message: 'Optimal solution found....'
solver: 'intlinprog'
整数制約のない問題の場合は、5 番目の出力として空でないラグランジュ乗数構造体も取得できます。
インデックス変数による解の表示
名前付きインデックス変数を使用して、最適化問題を作成して解きます。問題は、収益で重み付けされた、さまざまな空港へのフルーツのフローを最大化することです。これはそれぞれの重み付きフローへの制約に従います。
rng(0) % For reproducibility p = optimproblem('ObjectiveSense', 'maximize'); flow = optimvar('flow', ... {'apples', 'oranges', 'bananas', 'berries'}, {'NYC', 'BOS', 'LAX'}, ... 'LowerBound',0,'Type','integer'); p.Objective = sum(sum(rand(4,3).*flow)); p.Constraints.NYC = rand(1,4)*flow(:,'NYC') <= 10; p.Constraints.BOS = rand(1,4)*flow(:,'BOS') <= 12; p.Constraints.LAX = rand(1,4)*flow(:,'LAX') <= 35; sol = solve(p);
Solving problem using intlinprog.
LP: Optimal objective value is 1027.472366.
Heuristics: Found 1 solution using ZI round.
Lower bound is 1027.233133.
Relative gap is 0.00%.
Optimal solution found.
Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0. The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05.
ニューヨークとロサンゼルスへのオレンジとベリーの最適フローを求めます。
[idxFruit,idxAirports] = findindex(flow, {'oranges','berries'}, {'NYC', 'LAX'})idxFruit = 1×2
2 4
idxAirports = 1×2
1 3
orangeBerries = sol.flow(idxFruit, idxAirports)
orangeBerries = 2×2
0 980
70 0
この表示は、NYC 向けのオレンジは 0、70 のベリーが NYC 向け、980 のオレンジが LAX 向けで、LAX 向けのベリーは 0 であることを示しています。
次の最適なフローをリストします。
Fruit Airports
----- --------
Berries NYC
Apples BOS
Oranges LAX
idx = findindex(flow, {'berries', 'apples', 'oranges'}, {'NYC', 'BOS', 'LAX'})idx = 1×3
4 5 10
optimalFlow = sol.flow(idx)
optimalFlow = 1×3
70 28 980
この表示は、70 のベリーが NYC 向け、28 のアップルが BOS 向けで、980 のオレンジが LAX 向けであることを示しています。
非線形方程式系の解法、問題ベース
次の非線形方程式系を解きます。
問題ベースのアプローチを使用する場合は、まず x を 2 要素の最適化変数として定義します。
x = optimvar('x',2);最初の方程式を最適化等式として作成します。
eq1 = exp(-exp(-(x(1) + x(2)))) == x(2)*(1 + x(1)^2);
同様に、2 番目の方程式も最適化等式として作成します。
eq2 = x(1)*cos(x(2)) + x(2)*sin(x(1)) == 1/2;
方程式問題を作成し、方程式を問題に配置します。
prob = eqnproblem; prob.Equations.eq1 = eq1; prob.Equations.eq2 = eq2;
問題を確認します。
show(prob)
EquationProblem :
Solve for:
x
eq1:
exp((-exp((-(x(1) + x(2)))))) == (x(2) .* (1 + x(1).^2))
eq2:
((x(1) .* cos(x(2))) + (x(2) .* sin(x(1)))) == 0.5
点 [0,0] から始めて問題を解きます。問題ベースのアプローチの場合、初期点を構造体として指定します。変数名は構造体のフィールドとします。この問題の変数は x の 1 つしかありません。
x0.x = [0 0]; [sol,fval,exitflag] = solve(prob,x0)
Solving problem using fsolve. Equation solved. fsolve completed because the vector of function values is near zero as measured by the value of the function tolerance, and the problem appears regular as measured by the gradient.
sol = struct with fields:
x: [2x1 double]
fval = struct with fields:
eq1: -2.4070e-07
eq2: -3.8255e-08
exitflag =
EquationSolved
解の点を表示します。
disp(sol.x)
0.3532
0.6061
fcn2optimexpr を必要とするサポートされていない関数
方程式の関数が初等関数で構成されていない場合、fcn2optimexprを使用して、その関数を最適化式に変換しなければなりません。次に例を示します。
ls1 = fcn2optimexpr(@(x)exp(-exp(-(x(1)+x(2)))),x); eq1 = ls1 == x(2)*(1 + x(1)^2); ls2 = fcn2optimexpr(@(x)x(1)*cos(x(2))+x(2)*sin(x(1)),x); eq2 = ls2 == 1/2;
詳細については、最適化変数および式でサポートされる演算と非線形関数から最適化式への変換を参照してください。
入力引数
prob — 最適化問題または方程式問題
OptimizationProblem オブジェクト | EquationProblem オブジェクト
最適化問題または方程式問題。OptimizationProblem オブジェクトまたは EquationProblem オブジェクトとして指定します。最適化問題は optimproblem を使用して作成し、方程式問題は eqnproblem を使用して作成します。
警告
問題ベースのアプローチでは、目的関数、非線形等式、または非線形不等式における複素数値をサポートしていません。関数の計算に複素数値が含まれていると、それが中間値としてであっても、最終結果が不正確になる場合があります。
例: prob = optimproblem; prob.Objective = obj; prob.Constraints.cons1 = cons1;
例: prob = eqnproblem; prob.Equations = eqs;
x0 — 初期点
構造体 | OptimizationValues オブジェクトのベクトル
初期点。prob の変数名に等しいフィールド名をもつ構造体として指定します。
一部の Global Optimization Toolbox ソルバーでは、x0 を複数の初期点を表す OptimizationValues オブジェクトのベクトルにすることができます。関数 optimvalues を使用して、点を作成します。これらのソルバーには次のものがあります。
ga(Global Optimization Toolbox)、gamultiobj(Global Optimization Toolbox)、paretosearch(Global Optimization Toolbox)、およびparticleswarm(Global Optimization Toolbox)。これらのソルバーは、初期母集団のメンバーとして複数の開始点を受け入れます。MultiStart(Global Optimization Toolbox).このソルバーは、fminconなどのローカル ソルバーの複数の初期点を受け入れます。surrogateopt(Global Optimization Toolbox).このソルバーは、初期代理の生成に有効な複数の初期点を受け入れます。
名前付きインデックス変数と共に x0 を使用する例については、名前付きインデックス変数による最適化の初期点の作成を参照してください。
例: prob に変数 x と y がある場合: x0.x = [3,2,17]; x0.y = [pi/3,2*pi/3]
データ型: struct
ms — 複数開始点のソルバー
MultiStart オブジェクト | GlobalSearch オブジェクト
複数開始点のソルバー。MultiStart (Global Optimization Toolbox) オブジェクトまたは GlobalSearch (Global Optimization Toolbox) オブジェクトとして指定します。MultiStart コマンドまたは GlobalSearch コマンドを使用して、ms を作成します。
現在、GlobalSearch は fmincon ローカル ソルバーのみをサポートし、MultiStart は fmincon、fminunc、および lsqnonlin の各ローカル ソルバーのみをサポートしています。
例: ms = MultiStart;
例: ms = GlobalSearch(FunctionTolerance=1e-4);
名前と値の引数
引数の任意のペアを Name1=Value1,...,NameN=ValueN のように指定します。Name は引数名、Value は対応する値です。名前と値の引数は、他の引数より後に指定されている必要があります。ただし、各ペアの順序は任意です。
R2021a 以前では、それぞれの名前と値をコンマで区切り、Name を引用符で囲みます。
例: solve(prob,'Options',opts)
MinNumStartPoints — MultiStart の開始点の最小数
20 (既定値) | 正の整数
MultiStart (Global Optimization Toolbox) の開始点の最小数。正の整数として指定します。この引数は、ms 引数を使用して solve を呼び出す場合にのみ適用されます。solve は x0 のすべての値を開始点として使用します。MinNumStartPoints が x0 の値の数より大きい場合、solve は問題の範囲内でランダムかつ一様に多くの開始点を生成します。成分が非有界の場合、solve は MultiStart の既定の疑似境界を使用して点を生成します。
例: solve(prob,x0,ms,MinNumStartPoints=50)
データ型: double
Options — 最適化オプション
optimoptions によって作成されたオブジェクト | オプション構造体
最適化オプション。optimoptions で作成したオブジェクトまたはオプション構造体 (optimset で作成したものなど) として指定します。
'solver' 引数のリファレンスで詳しく述べているとおり、関数 solve は内部的に、関連するソルバーを呼び出します。options にソルバーとの互換性があることを確認します。たとえば、intlinprog ではオプションを構造体にすることはできません。lsqnonneg ではオプションをオブジェクトにすることはできません。
intlinprog の解または解を求める速度を改善するためのオプション設定については、整数線形計画法の調整を参照してください。linprog の場合、既定の 'dual-simplex' アルゴリズムの方が、一般にメモリ効率が高く、迅速です。状況によっては、Algorithm オプションが 'interior-point' の場合に、linprog が大規模な問題をより迅速に解くことがあります。非線形問題の解を改善するためのオプション設定については、一般的に使用される最適化オプション: 調整とトラブルシューティングおよび結果の向上を参照してください。
例: options = optimoptions('intlinprog','Display','none')
Solver — 最適化ソルバー
'intlinprog' | 'linprog' | 'lsqlin' | 'lsqcurvefit' | 'lsqnonlin' | 'lsqnonneg' | 'quadprog' | 'fminbnd' | 'fminunc' | 'fmincon' | 'fminsearch' | 'fzero' | 'fsolve' | 'coneprog' | 'ga' | 'gamultiobj' | 'paretosearch' | 'patternsearch' | 'particleswarm' | 'surrogateopt' | 'simulannealbnd'
最適化ソルバー。リストされているソルバーの名前として指定します。以下の表には、最適化問題について、Global Optimization Toolbox のソルバーを含め、問題のタイプごとに使用可能なソルバーが示されています。方程式問題の詳細については、最適化ソルバーの詳細の後に示しています。
整数制約をもつ非線形問題を prob2struct で変換する場合、結果として得られる問題構造体は選択したソルバーに依存します。Global Optimization Toolbox ライセンスをお持ちでない場合は、このソルバーを指定する必要があります。詳細については、非線形問題ベースの最適化における整数制約を参照してください。
最適化問題のタイプごとに、既定のソルバーを以下の表に示します。
| 問題のタイプ | 既定のソルバー |
|---|---|
| 線形計画法 (LP) | linprog |
| 混合整数線形計画法 (MILP) | intlinprog |
| 二次計画法 (QP) | quadprog |
| 2 次錐計画法 (SOCP) | coneprog |
| 線形最小二乗法 | lsqlin |
| 非線形最小二乗法 | lsqnonlin |
| 非線形計画法 (NLP) | |
| 混合整数非線形計画法 (MINLP) | ga (Global Optimization Toolbox) |
| 多目的 | gamultiobj (Global Optimization Toolbox) |
次の表で、
はその問題のタイプにソルバーを使用できることを表し、"x" はソルバーを使用できないことを表しています。
問題のタイプ | LP | MILP | QP | SOCP | 線形最小二乗法 | 非線形最小二乗法 | NLP | MINLP |
|---|---|---|---|---|---|---|---|---|
| ソルバー | ||||||||
linprog |
| x | x | x | x | x | x | x |
intlinprog |
|
| x | x | x | x | x | x |
quadprog |
| x |
|
|
| x | x | x |
coneprog |
| x | x |
| x | x | x | x |
lsqlin | x | x | x | x |
| x | x | x |
lsqnonneg | x | x | x | x |
| x | x | x |
lsqnonlin | x | x | x | x |
|
| x | x |
fminunc |
| x |
| x |
|
|
| x |
fmincon |
| x |
|
|
|
|
| x |
fminbnd | x | x | x | x |
|
|
| x |
fminsearch | x | x | x | x |
|
|
| x |
patternsearch (Global Optimization Toolbox) |
| x |
|
|
|
|
| x |
ga (Global Optimization Toolbox) |
|
|
|
|
|
|
|
|
particleswarm (Global Optimization Toolbox) |
| x |
| x |
|
|
| x |
simulannealbnd (Global Optimization Toolbox) |
| x |
| x |
|
|
| x |
surrogateopt (Global Optimization Toolbox) |
|
|
|
|
|
|
|
|
gamultiobj (Global Optimization Toolbox) |
|
|
|
|
|
|
|
|
paretosearch (Global Optimization Toolbox) |
| x |
|
|
|
|
| x |
メモ
最小二乗問題のソルバーとして lsqcurvefit を選択した場合、solve は lsqnonlin を使用します。solve に関して lsqcurvefit ソルバーと lsqnonlin ソルバーは同一です。
注意
最大化問題 (prob.ObjectiveSense が "max" または "maximize") の場合は、最小二乗ソルバー (名前が lsq で始まるソルバー) を指定しないでください。これらのソルバーは最大化を実行できないので、指定すると solve でエラーが発生します。
以下の表には、方程式の求解について、問題のタイプごとに使用可能なソルバーが示されています。以下の表では、
* は、その問題のタイプの既定のソルバーを示します。
Y は、使用可能なソルバーを示します。
N は、使用できないソルバーを示します。
方程式でサポートされているソルバー
| 方程式のタイプ | lsqlin | lsqnonneg | fzero | fsolve | lsqnonlin |
|---|---|---|---|---|---|
| 線形 | * | N | Y (スカラーのみ) | Y | Y |
| 範囲付き線形 | * | Y | N | N | Y |
| スカラー非線形 | N | N | * | Y | Y |
| 非線形方程式系 | N | N | N | * | Y |
| 範囲付き非線形方程式系 | N | N | N | N | * |
例: 'intlinprog'
データ型: char | string
ObjectiveDerivative — 目的関数に自動微分を使用するための指示
'auto' (既定値) | 'auto-forward' | 'auto-reverse' | 'finite-differences'
非線形目的関数に対して自動微分 (AD) を使用するための指示。'auto' (可能な場合に AD を使用)、'auto-forward' (可能な場合にフォワード モードの AD を使用)、'auto-reverse' (可能な場合にリバース モードの AD を使用)、または 'finite-differences' (AD を使用しない) として指定します。最適化変数および式でサポートされる演算で説明されているように、目的関数がサポートされている場合は、auto などを選択すると、基礎となるソルバーが問題の求解時に勾配情報を使用するようになります。例については、問題ベースの最適化における自動微分の効果を参照してください。
ソルバーは既定で次のタイプの AD を選択します。
一般的な非線形目的関数の場合、
fminconは既定で目的関数用のリバース モードの AD になります。fminconは、非線形制約の数が変数の数よりも少ない場合に既定で非線形制約関数用のリバース モードの AD になります。それ以外の場合、fminconは既定で非線形制約関数用のフォワード モードの AD になります。一般的な非線形目的関数の場合、
fminuncは既定でリバース モードの AD になります。最小二乗目的関数の場合、
fminconとfminuncは既定で目的関数用のフォワード モードの AD になります。問題ベースの最小二乗目的関数の定義については、問題ベースの最小二乗法の目的関数の記述を参照してください。lsqnonlinは、目的ベクトルに含まれる要素数が変数の数以上である場合に既定でフォワード モードの AD になります。それ以外の場合、lsqnonlinは既定でリバース モードの AD になります。fsolveは、方程式の数が変数の数以上の場合に既定でフォワード モードの AD になります。それ以外の場合、fsolveは既定でリバース モードの AD になります。
例: 'finite-differences'
データ型: char | string
ConstraintDerivative — 制約関数に自動微分を使用するための指示
'auto' (既定値) | 'auto-forward' | 'auto-reverse' | 'finite-differences'
非線形制約関数に対して自動微分 (AD) を使用するための指示。'auto' (可能な場合に AD を使用)、'auto-forward' (可能な場合にフォワード モードの AD を使用)、'auto-reverse' (可能な場合にリバース モードの AD を使用)、または 'finite-differences' (AD を使用しない) として指定します。最適化変数および式でサポートされる演算で説明されているように、制約関数がサポートされている場合は、auto などを選択すると、基礎となるソルバーが問題の求解時に勾配情報を使用するようになります。例については、問題ベースの最適化における自動微分の効果を参照してください。
ソルバーは既定で次のタイプの AD を選択します。
一般的な非線形目的関数の場合、
fminconは既定で目的関数用のリバース モードの AD になります。fminconは、非線形制約の数が変数の数よりも少ない場合に既定で非線形制約関数用のリバース モードの AD になります。それ以外の場合、fminconは既定で非線形制約関数用のフォワード モードの AD になります。一般的な非線形目的関数の場合、
fminuncは既定でリバース モードの AD になります。最小二乗目的関数の場合、
fminconとfminuncは既定で目的関数用のフォワード モードの AD になります。問題ベースの最小二乗目的関数の定義については、問題ベースの最小二乗法の目的関数の記述を参照してください。lsqnonlinは、目的ベクトルに含まれる要素数が変数の数以上である場合に既定でフォワード モードの AD になります。それ以外の場合、lsqnonlinは既定でリバース モードの AD になります。fsolveは、方程式の数が変数の数以上の場合に既定でフォワード モードの AD になります。それ以外の場合、fsolveは既定でリバース モードの AD になります。
例: 'finite-differences'
データ型: char | string
EquationDerivative — 方程式に自動微分を使用するための指示
'auto' (既定値) | 'auto-forward' | 'auto-reverse' | 'finite-differences'
非線形制約関数に対して自動微分 (AD) を使用するための指示。'auto' (可能な場合に AD を使用)、'auto-forward' (可能な場合にフォワード モードの AD を使用)、'auto-reverse' (可能な場合にリバース モードの AD を使用)、または 'finite-differences' (AD を使用しない) として指定します。最適化変数および式でサポートされる演算で説明されているように、方程式関数がサポートされている場合は、auto などを選択すると、基礎となるソルバーが問題の求解時に勾配情報を使用するようになります。例については、問題ベースの最適化における自動微分の効果を参照してください。
ソルバーは既定で次のタイプの AD を選択します。
一般的な非線形目的関数の場合、
fminconは既定で目的関数用のリバース モードの AD になります。fminconは、非線形制約の数が変数の数よりも少ない場合に既定で非線形制約関数用のリバース モードの AD になります。それ以外の場合、fminconは既定で非線形制約関数用のフォワード モードの AD になります。一般的な非線形目的関数の場合、
fminuncは既定でリバース モードの AD になります。最小二乗目的関数の場合、
fminconとfminuncは既定で目的関数用のフォワード モードの AD になります。問題ベースの最小二乗目的関数の定義については、問題ベースの最小二乗法の目的関数の記述を参照してください。lsqnonlinは、目的ベクトルに含まれる要素数が変数の数以上である場合に既定でフォワード モードの AD になります。それ以外の場合、lsqnonlinは既定でリバース モードの AD になります。fsolveは、方程式の数が変数の数以上の場合に既定でフォワード モードの AD になります。それ以外の場合、fsolveは既定でリバース モードの AD になります。
例: 'finite-differences'
データ型: char | string
出力引数
アルゴリズム
拡張機能
バージョン履歴
R2017b で導入
You can also select a web site from the following list:
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)