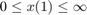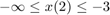このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

patternsearch

パターン検索を使用して関数の最小値を見つける

ページ内をすべて折りたたむ

構文

x = patternsearch(fun,x0)

x = patternsearch(fun,x0,A,b)

x = patternsearch(fun,x0,A,b,Aeq,beq)

x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub)

x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

x = patternsearch(problem)

[x,fval] = patternsearch(___)

[x,fval,exitflag,output] = patternsearch(___)

説明

x = patternsearch(fun,x0) は、目的関数の値を計算する関数ハンドル fun の局所最小値 x を見つけます。x0 は、パターン検索アルゴリズムの初期点を指定する実数ベクトルです。

メモ

追加パラメーターの受け渡しは、必要に応じて他のパラメーターを目的関数と非線形制約関数に渡す方法を説明します。

例

x = patternsearch(fun,x0,A,b) は、線形不等式 A*x ≤ b を条件として fun を最小化します。線形不等式制約を参照してください。

例

x = patternsearch(fun,x0,A,b,Aeq,beq) は、線形等式 Aeq*x = beq および A*x ≤ b に従って fun を最小化します。線形不等式が存在しない場合は、A = [] と b = [] を設定します。

x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub) は、解が常に lb ≤ x ≤ ub の範囲に存在するように、設計変数 x に上限と下限を定義します。線形等式が存在しない場合は、Aeq = [] と beq = [] を設定します。x(i) に下限がない場合は、 lb(i) = -Inf を設定します。x(i) に上限がない場合は、 ub(i) = Inf を設定します。

例

x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) は、 nonlcon で定義された非線形不等式 c(x) または等式 ceq(x) に従って最小化を行います。 patternsearch は、 c(x) ≤ 0 および ceq(x) = 0 となるように fun を最適化します。境界が存在しない場合は、lb = []、ub = []、またはその両方を設定します。

例

x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) は、options で指定された最適化オプションを使って fun を最小化します。optimoptions を使用してこれらのオプションを設定してください。非線形不等式制約または非線形等式制約がない場合は nonlcon = [] を設定します。

例

x = patternsearch(problem) は、problem で説明されている構造体 problem の最小値を求めます。

[x,fval] = patternsearch(___) は、どの構文でも、解 x での目的関数 fun の値を返します。

例

[x,fval,exitflag,output] = patternsearch(___) はさらに、patternsearch の終了条件を記述する値である exitflag と、最適化プロセスに関する情報を含む構造体 output を返します。

例

すべて折りたたむ

制約なしパターン探索最小化

スクリプトを開く

patternsearch ソルバーを使用して制約のない問題を最小化します。

次の 2 変数の目的関数を作成します。MATLAB® パスで、次のコードを psobj.m という名前のファイルに保存します。

function y = psobj(x)

y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));

目的関数を @psobj に設定します。

fun = @psobj;

点 [0,0] から始めて、最小値を見つけます。

x0 = [0,0];
x = patternsearch(fun,x0)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

x =

   -0.7037   -0.1860

線形不等式制約によるパターン検索

スクリプトを開く

いくつかの線形不等式制約に従って関数を最小化します。

次の 2 変数の目的関数を作成します。MATLAB® パスで、次のコードを psobj.m という名前のファイルに保存します。

function y = psobj(x)

y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));

目的関数を @psobj に設定します。

fun = @psobj;

2 つの線形不等式制約を設定します。

A = [-3,-2;
    -4,-7];
b = [-1;-8];

点 [0.5,-0.5] から始めて、最小値を見つけます。

x0 = [0.5,-0.5];
x = patternsearch(fun,x0,A,b)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

x =

    5.2827   -1.8758

境界付きパターン検索

スクリプトを開く

制限された制約のみを持つ関数の最小値を見つけます。

次の 2 変数の目的関数を作成します。MATLAB® パスで、次のコードを psobj.m という名前のファイルに保存します。

function y = psobj(x)

y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));

目的関数を @psobj に設定します。

fun = @psobj;

$0 \le x(1) \le\infty$ と $-\infty \le x(2) \le -3$ のときの最小値を見つけます。

lb = [0,-Inf];
ub = [Inf,-3];
A = [];
b = [];
Aeq = [];
beq = [];

点 [1,-5] から始めて、最小値を見つけます。

x0 = [1,-5];
x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

x =

    0.1880   -3.0000

非線形制約によるパターン検索

スクリプトを開く

非線形不等式制約に従う関数の最小値を見つけます。

次の 2 変数の目的関数を作成します。MATLAB® パスで、次のコードを psobj.m という名前のファイルに保存します。

function y = psobj(x)

y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));

目的関数を @psobj に設定します。

fun = @psobj;

非線形制約を作成する

$\frac{{xy}}{2} + {\left( {x + 2} \right)^2} + \frac{{{{\left( {y - 2}
\right)}^2}}}{2} \le 2.$

これを行うには、MATLAB パスで、次のコードを ellipsetilt.m という名前のファイルに保存します。

function [c,ceq] = ellipsetilt(x)
ceq = [];
c = x(1)*x(2)/2 + (x(1)+2)^2 + (x(2)-2)^2/2 - 2;

初期点[-2,-2]からpatternsearchを開始します。

x0 = [-2,-2];
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = @ellipsetilt;
x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

Optimization finished: mesh size less than options.MeshTolerance 
and constraint violation is less than options.ConstraintTolerance.

x =

   -1.5144    0.0875

さまざまな`patternsearch`アルゴリズムを試す

ライブスクリプトを開く

場合によっては、異なる patternsearch アルゴリズムの動作が著しく異なることがあります。どのアルゴリズムが問題に最適かを予測するのは難しいかもしれませんが、さまざまなアルゴリズムを簡単に試すことができます。この例では、この例を実行するときに使用できる sawtoothxy 目的関数を使用します。この関数は、全体的または複数の局所的最小値を見つけるで説明およびプロットされています。

type sawtoothxy

function f = sawtoothxy(x,y)
[t r] = cart2pol(x,y); % change to polar coordinates
h = cos(2*t - 1/2)/2 + cos(t) + 2;
g = (sin(r) - sin(2*r)/2 + sin(3*r)/3 - sin(4*r)/4 + 4) ...
    .*r.^2./(r+1);
f = g.*h;
end

この目的関数を最小化する際のさまざまなアルゴリズムの動作を確認するには、非対称の境界をいくつか設定します。また、真の解 sol = [0 0] から離れた初期点 x0 を設定します (sawtoothxy(0,0) = 0 )。

rng default
x0 = 12*randn(1,2);
lb = [-15,-26];
ub = [26,15];
fun = @(x)sawtoothxy(x(1),x(2));

"classic" patternsearch アルゴリズムを使用して sawtoothxy 関数を最小化します。

optsc = optimoptions("patternsearch",Algorithm="classic");
[sol,fval,eflag,output] = patternsearch(fun,...
    x0,[],[],[],[],lb,ub,[],optsc)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

sol = 1×2
10^-5 ×

    0.9825         0

fval = 1.3278e-09

eflag = 1

output = struct with fields:
         function: @(x)sawtoothxy(x(1),x(2))
      problemtype: 'boundconstraints'
       pollmethod: 'gpspositivebasis2n'
    maxconstraint: 0
     searchmethod: []
       iterations: 52
        funccount: 168
         meshsize: 9.5367e-07
         rngstate: [1x1 struct]
          message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'

"classic" アルゴリズムは、52 回の反復と 168 回の関数評価でグローバルソリューションに到達します。

"nups" アルゴリズムを試してください。

rng default % For reproducibility
optsn = optimoptions("patternsearch",Algorithm="nups");
[sol,fval,eflag,output] = patternsearch(fun,...
    x0,[],[],[],[],lb,ub,[],optsn)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

sol = 1×2

    6.3204   15.0000

fval = 85.9256

eflag = 1

output = struct with fields:
         function: @(x)sawtoothxy(x(1),x(2))
      problemtype: 'boundconstraints'
       pollmethod: 'nups'
    maxconstraint: 0
     searchmethod: []
       iterations: 29
        funccount: 88
         meshsize: 7.1526e-07
         rngstate: [1x1 struct]
          message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'

今回は、ソルバーはわずか 29 回の反復と 88 回の関数評価でローカルソリューションに到達しますが、そのソリューションはグローバルソリューションではありません。

座標方向にステップを踏まない "nups-mads" アルゴリズムを使用してみてください。

rng default % For reproducibility
optsm = optimoptions("patternsearch",Algorithm="nups-mads");
[sol,fval,eflag,output] = patternsearch(fun,...
    x0,[],[],[],[],lb,ub,[],optsm)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

sol = 1×2
10^-4 ×

   -0.5275    0.0806

fval = 1.5477e-08

eflag = 1

output = struct with fields:
         function: @(x)sawtoothxy(x(1),x(2))
      problemtype: 'boundconstraints'
       pollmethod: 'nups-mads'
    maxconstraint: 0
     searchmethod: []
       iterations: 55
        funccount: 189
         meshsize: 9.5367e-07
         rngstate: [1x1 struct]
          message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'

今回は、ソルバーは 55 回の反復と 189 回の関数評価でグローバルソリューションに到達します。これは、'classic' アルゴリズムに似ています。

デフォルト以外のオプションを使用したパターン検索

patternsearch ソリューションプロセスの進行状況を観察するためのオプションを設定します。

次の 2 変数の目的関数を作成します。MATLAB^® パスで、次のコードを psobj.m という名前のファイルに保存します。

function y = psobj(x)

y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));

目的関数を @psobj に設定します。

fun = @psobj;

反復表示を行い、各反復で目的関数をプロットするには、options を設定します。

options = optimoptions('patternsearch','Display','iter','PlotFcn',@psplotbestf);

点 [0,0] から始めて、目的の制約のない最小値を見つけます。

x0 = [0,0];
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

Iter     f-count          f(x)      MeshSize     Method
    0        1              1             1      
    1        4       -5.88607             2     Successful Poll
    2        8       -5.88607             1     Refine Mesh
    3       12       -5.88607           0.5     Refine Mesh
    4       16       -5.88607          0.25     Refine Mesh

(output trimmed)

   63      218       -7.02545     1.907e-06     Refine Mesh
   64      221       -7.02545     3.815e-06     Successful Poll
   65      225       -7.02545     1.907e-06     Refine Mesh
   66      229       -7.02545     9.537e-07     Refine Mesh
Optimization terminated: mesh size less than options.MeshTolerance.

x =

   -0.7037   -0.1860

関数値と最小点を取得する

スクリプトを開く

関数の最小値を見つけ、最小値の位置と値の両方を報告します。

次の 2 変数の目的関数を作成します。MATLAB® パスで、次のコードを psobj.m という名前のファイルに保存します。

function y = psobj(x)

y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));

目的関数を @psobj に設定します。

fun = @psobj;

点 [0,0] から始めて、目的の制約のない最小値を見つけます。最小値 x の位置と fun(x) の値の両方を返します。

x0 = [0,0];
[x,fval] = patternsearch(fun,x0)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

x =

   -0.7037   -0.1860


fval =

   -7.0254

すべての出力の取得

スクリプトを開く

patternsearch 解決プロセスを調べるには、すべての出力を取得します。

次の 2 変数の目的関数を作成します。MATLAB® パスで、次のコードを psobj.m という名前のファイルに保存します。

function y = psobj(x)

y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));

目的関数を @psobj に設定します。

fun = @psobj;

点 [0,0] から始めて、目的の制約のない最小値を見つけます。解x、解における目的関数値fun(x)、終了フラグ、および出力構造を返します。

x0 = [0,0];
[x,fval,exitflag,output] = patternsearch(fun,x0)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

x =

   -0.7037   -0.1860


fval =

   -7.0254


exitflag =

     1


output = 

  struct with fields:

         function: @psobj
      problemtype: 'unconstrained'
       pollmethod: 'gpspositivebasis2n'
    maxconstraint: []
     searchmethod: []
       iterations: 66
        funccount: 229
         meshsize: 9.5367e-07
         rngstate: [1x1 struct]
          message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'

exitflag は 1 であり、局所的最小値への収束を示します。

output 構造には、patternsearch が何回反復したか、関数が何回評価されたかなどの情報が含まれています。この出力構造をデフォルト以外のオプションを使用したパターン検索の結果と比較してください。この例では、この情報の一部は取得されますが、たとえば関数評価の回数は取得されません。

入力引数

すべて折りたたむ

`fun` — 最小化される機能
関数ハンドル | 関数名

最小化する関数。関数ハンドルまたは関数名として指定します。fun 関数はベクトル x を受け取り、実数スカラー f を返します。これは x で評価された目的関数です。

ファイルの関数ハンドルとしてfunを指定できます

x = patternsearch(@myfun,x0)

ここで、myfunは次のようなMATLAB関数である。

function f = myfun(x)
f = ...            % Compute function value at x

funは匿名関数の関数ハンドルにもなります

x = patternsearch(@(x)norm(x)^2,x0,A,b);

例: fun = @(x)sin(x(1))*cos(x(2))

データ型: char | function_handle | string

`x0` — 初期点
実数ベクトル

初期点。実数ベクトルとして指定されます。patternsearch は、x0 の要素数を使用して、fun が受け入れる変数の数を決定します。

例: x0 = [1,2,3,4]

データ型: double

`A` — 線形不等式制約
実数行列

線形不等式制約。実数行列として指定されます。A は M 行 nvars 列の行列で、M は不等式の数です。

A は M 個の線形不等式を符号化します。

A*x <= b,

ここで、x は nvars 個の変数 x(:) の列ベクトル、b は M 個の要素をもつ列ベクトルです。

例えば、

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

次の制約を与えます:

A = [1,2;3,4;5,6];
b = [10;20;30];

例: 制御変数の合計が 1 以下になるように指定するには、制約 A = ones(1,N) と b = 1 を指定します。

データ型: double

`b` — 線形不等式制約
実数ベクトル

実数ベクトルで指定される線形不等式制約です。b は、行列 A に関連する M 要素ベクトルです。b を行ベクトルとして渡す場合、ソルバーは b を列ベクトル b(:) に内部的に変換します。

b は M 個の線形不等式を符号化します。

A*x <= b,

ここで、x は N 個の変数 x(:) の列ベクトル、A は M 行 N 列の行列です。

例えば、

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

次の制約を与えます:

A = [1,2;3,4;5,6];
b = [10;20;30];

例: 制御変数の合計が 1 以下になるように指定するには、制約 A = ones(1,N) と b = 1 を指定します。

データ型: double

`Aeq` — 線形等式制約
実数行列

線形等式制約。実数行列として指定されます。Aeq は Me 行 nvars 列の行列で、Me は等式の数です。

Aeq は Me 個の線形等式を符号化します。

Aeq*x = beq,

ここで、x は N 個の変数 x(:) の列ベクトル、beq は Me 個の要素をもつ列ベクトルです。

例えば、

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

次の制約を与えます:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

例: 制御変数の合計が 1 になるように指定するには、制約 Aeq = ones(1,N) と beq = 1 を指定します。

データ型: double

`beq` — 線形等式制約
実数ベクトル

実数ベクトルで指定される線形等式制約です。beq は、行列 Aeq に関連する Me 要素ベクトルです。beq を行ベクトルとして渡す場合、ソルバーは beq を列ベクトル beq(:) に内部的に変換します。

beq は Me 個の線形等式を符号化します。

Aeq*x = beq,

ここで、x は N 個の変数 x(:) の列ベクトル、Aeq は Meq 行 N 列の行列です。

例えば、

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

次の制約を与えます:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

例: 制御変数の合計が 1 になるように指定するには、制約 Aeq = ones(1,N) と beq = 1 を指定します。

データ型: double

`lb` — 下限
実数ベクトル | 実数配列

下限。実数ベクトルまたは実数配列として指定されます。x0の要素数がlbの要素数と等しい場合、lbは

x(i) >= lb(i)

これは、すべての i についてです。

numel(lb) < numel(x0) の場合、lb は次を指定します。

x(i) >= lb(i)

for

1 <= i <= numel(lb)

この場合、ソルバーによって警告が発行されます。

例: すべての制御変数が正であることを指定するには、lb = zeros(size(x0))

データ型: double

`ub` — 上限
実数ベクトル | 実数配列

実数ベクトルまたは実数配列として指定される上限です。x0の要素数がubの要素数と等しい場合、ubは

x(i) <= ub(i)

これは、すべての i についてです。

numel(ub) < numel(x0) の場合、ub は次を指定します。

x(i) <= ub(i)

for

1 <= i <= numel(ub)

この場合、ソルバーによって警告が発行されます。

例: すべての制御変数が1未満であることを指定するには、ub = ones(size(x0))

データ型: double

`nonlcon` — 非線形制約
関数ハンドル | 関数名

非線形制約。関数ハンドルまたは関数名として指定されます。nonlcon は、ベクトルまたは配列 x を受け、2 つの配列 c(x) および ceq(x) を返す関数です。

c(x) は、x での非線形不等式制約の配列です。patternsearch は次の条件を満たそうとします。
c(x) <= 0
c のすべてのエントリについて。
ceq(x) は、x での非線形等式制約の配列です。patternsearch は次の条件を満たそうとします。
ceq(x) = 0
ceq のすべてのエントリについて。

以下に例を示します。

x = patternsearch(@myfun,x0,A,b,Aeq,beq,lb,ub,@mycon)

ここで mycon は次のような MATLAB 関数です。

function [c,ceq] = mycon(x)
c = ...     % Compute nonlinear inequalities at x.
ceq = ...   % Compute nonlinear equalities at x.

詳細については、非線形制約を参照してください。

データ型: char | function_handle | string

`options` — 最適化オプション
`optimoptions` によって返されるオブジェクト | 構造体

最適化オプション。optimoptions によって返されるオブジェクト (推奨)、または構造体として指定されます。

次の表は最適化オプションについて説明しています。optimoptions は、斜体で示されたオプションを非表示にします。optimoptions で非表示になっているオプションを参照してください。{} はデフォルト値を示します。オプションの詳細については、パターン検索オプションを参照してください。

patternsearch のオプション

オプション	説明	値
`Algorithm`	`patternsearch` が使用するアルゴリズム。`Algorithm` 設定は利用可能なオプションに影響します。アルゴリズムの詳細については、パターン検索ポーリングの仕組みおよび非一様パターン検索 (NUPS) アルゴリズムを参照してください。アルゴリズムの効果の例については、patternsearch アルゴリズムを調べるとライブエディタータスクの最適化における patternsearch アルゴリズムの調査を参照してください。	`{"classic"}` \| `"nups"` \| `"nups-gps"` \| `"nups-mads"`
Cache	`Cache` を `"on"` に設定すると、`patternsearch` はポーリングするメッシュポイントの履歴を保持します。後続の反復では、`patternsearch` はすでにポーリングされたポイントに近いポイントをポーリングしません。目的関数の計算中に `patternsearch` の実行速度が遅い場合は、このオプションを使用します。目的関数が確率的である場合は、このオプションを使用しないでください。メモ `Cache` は、ソルバーを並列で実行すると機能しません。	`"on"` \| `{"off"}`
CacheSize	履歴のサイズ。	非負のスカラー \| `{1e4}`
CacheTol	`patternsearch` が現在のポイントをポーリングしないようにするための、現在のメッシュポイントから履歴内の任意のポイントまでの最大距離。`Cache` オプションが `"on"` に設定されている場合に使用します。	非負のスカラー \| `{eps}`
`ConstraintTolerance`	制約に対する許容度。オプション構造の場合は、`TolCon` を使用します。	正のスカラー \| `{1e-6}`
`Display`	表示レベル。つまり、解決プロセス中に `patternsearch` がコマンドラインに返す情報の量です。	`"off"` \| `"iter"` \| `"diagnose"` \| `{"final"}`
`FunctionTolerance`	関数の許容範囲。関数値の変化が `FunctionTolerance` 未満で、メッシュサイズが `StepTolerance` 未満の場合、反復は停止します。このオプションは、MADS (メッシュアダプティブダイレクトサーチ) ポーリングには適用されません。オプション構造の場合は、`TolFun` を使用します。	非負のスカラー \| `{1e-6}`
`InitialMeshSize`	アルゴリズムの初期メッシュサイズ。パターン検索ポーリングの仕組みを参照してください。	正のスカラー \| `{1.0}`
InitialPenalty	ペナルティパラメータの初期値。パターン探索のための非線形制約ソルバーアルゴリズムを参照してください。	正のスカラー \| `{10}`
`MaxFunctionEvaluations`	目的関数評価の最大数。オプション構造の場合は、`MaxFunEvals` を使用します。	非負整数 \| `{"2000*numberOfVariables"}`、`numberOfVariables`は問題変数の数
`MaxIterations`	反復最大回数オプション構造の場合は、`MaxIter` を使用します。	非負整数 \| `{"100*numberOfVariables"}`、`numberOfVariables`は問題変数の数
MaxMeshSize	ポーリングまたは検索ステップで使用される最大メッシュサイズ。パターン検索ポーリングの仕組みを参照してください。	非負のスカラー \| `{Inf}`
`MaxTime`	最適化に許可される合計時間 (秒単位)。オプション構造の場合は、`TimeLimit` を使用します。	非負のスカラー \| `{Inf}`
`MeshContractionFactor`	失敗した反復のメッシュ収縮係数。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。オプション構造の場合は、`MeshContraction` を使用します。	正のスカラー \| `{0.5}`
`MeshExpansionFactor`	反復を成功させるためのメッシュ拡張係数。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。オプション構造の場合は、`MeshExpansion` を使用します。	正のスカラー \| `{2.0}`
MeshRotate	ポイントが最適であると宣言する前にパターンを回転させるフラグ。メッシュオプションを参照してください。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。	`"off"` \| `{"on"}`
`MeshTolerance`	メッシュサイズの許容範囲。オプション構造の場合は、`TolMesh` を使用します。	非負のスカラー \| `{1e-6}`
`OutputFcn`	各反復で最適化関数によって呼び出される関数。関数ハンドルまたは関数ハンドルのセル配列として指定します。オプション構造の場合は、`OutputFcns` を使用します。	関数ハンドルまたは関数ハンドルのセル配列 \| `{[]}`
PenaltyFactor	ペナルティ更新パラメータ。パターン探索のための非線形制約ソルバーアルゴリズムを参照してください。	正のスカラー \| `{100}`
`PlotFcn`	パターン検索からの出力のプロット。組み込みプロット関数の名前、関数ハンドル、または組み込みプロット関数または関数ハンドルの名前のセル配列として指定します。オプション構造の場合は、`PlotFcns` を使用します。	`{[]}` \| `"psplotbestf"` \| `"psplotfuncount"` \| `"psplotmeshsize"` \| `"psplotbestx"` \| `"psplotmaxconstr"` \| カスタムプロット関数
PlotInterval	プロットの反復回数。`1` は反復ごとにプロットすることを意味し、`2` は 1 回おきの反復ごとにプロットすることを意味します。	正の整数 \| `{1}`
`PollMethod`	パターン検索で使用されるポーリング戦略。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。メモ問題に線形等式制約がある場合は、MADS ポーリングは使用できません。	`{"GPSPositiveBasis2N"}` `\|` `"GPSPositiveBasisNp1"` `\|` `"GSSPositiveBasis2N"` `\|` `"GSSPositiveBasisNp1"` `\|` `"MADSPositiveBasis2N"` `\|` `"MADSPositiveBasisNp1"`
`PollOrderAlgorithm`	パターン検索におけるポーリング方向の順序。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。オプション構造の場合は、`PollingOrder` を使用します。	`"Random"` \| `"Success"` \| `{"Consecutive"}`
`ScaleMesh`	変数の自動スケーリング。オプション構造の場合は、`ScaleMesh` = `"on"` または `"off"` を使用します。	`{true}`\| `false`
`SearchFcn`	パターン検索で使用される検索のタイプ。名前または関数ハンドルとして指定します。オプション構造の場合は、`SearchMethod` を使用します。	`"GPSPositiveBasis2N" \| "GPSPositiveBasisNp1" \| "GSSPositiveBasis2N" \| "GSSPositiveBasisNp1" \| "MADSPositiveBasis2N" \| "MADSPositiveBasisNp1" \| "searchga" \| "searchlhs" \| "searchneldermead" \| "rbfsurrogate" \| {[]} \|` カスタム検索機能
`StepTolerance`	変数の許容範囲。位置の変化とメッシュサイズの両方が `StepTolerance` 未満の場合、反復は停止します。このオプションはMADSポーリングには適用されません。オプション構造の場合は、`TolX` を使用します。	非負のスカラー \| `{1e-6}`
TolBind	バインディング許容度。制約パラメータを参照してください。	非負のスカラー \| `{1e-3}`
`UseCompletePoll`	現在のポイントの周りの投票を完了するためのフラグ。パターン検索ポーリングの仕組みを参照してください。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。メモ `"classic"` アルゴリズムの場合、ベクトル化または並列ポーリングのために `UseCompletePoll` を `true` に設定する必要があります。同様に、ベクトル化または並列検索の場合は `UseCompleteSearch` を `true` に設定します。 R2019a 以降では、`UseParallel` オプションを `true` に設定すると、`patternsearch` が内部的に `UseCompletePoll` 設定を `true` にオーバーライドし、関数が並列にポーリングするようになります。オプション構造の場合は、`CompletePoll` = `"on"` または `"off"` を使用します。	`true` \| `{false}`
`UseCompleteSearch`	検索方法がポーリング方式の場合に、現在のポイントの周囲での検索を完了するためのフラグ。検索と投票を参照してください。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。メモ `"classic"` アルゴリズムの場合、ベクトル化または並列検索のために `UseCompleteSearch` を `true` に設定する必要があります。オプション構造の場合は、`CompleteSearch` = `"on"` または `"off"` を使用します。	`true` \| `{false}`
`UseParallel`	目的関数と非線形制約関数を並列に計算するためのフラグ。ベクトル化と並列化のオプションおよびGlobal Optimization Toolbox で並列処理を使用する方法を参照してください。メモ `"classic"` アルゴリズムの場合、ベクトル化または並列ポーリングのために `UseCompletePoll` を `true` に設定する必要があります。同様に、ベクトル化または並列検索の場合は `UseCompleteSearch` を `true` に設定します。 R2019a 以降では、`UseParallel` オプションを `true` に設定すると、`patternsearch` が内部的に `UseCompletePoll` 設定を `true` にオーバーライドし、関数が並列にポーリングするようになります。メモ `Cache` は、ソルバーを並列で実行すると機能しません。	`true` \| `{false}`
`UseVectorized`	関数がベクトル化されるかどうかを指定します。ベクトル化と並列化のオプションおよび目的関数と制約関数をベクトル化するを参照してください。メモ `"classic"` アルゴリズムの場合、ベクトル化または並列ポーリングのために `UseCompletePoll` を `true` に設定する必要があります。同様に、ベクトル化または並列検索の場合は `UseCompleteSearch` を `true` に設定します。オプション構造の場合は、`Vectorized` = `"on"` または `"off"` を使用します。	`true` \| `{false}`

例: options = optimoptions("patternsearch",MaxIterations=150,MeshTolerance=1e-4)

`problem` — 問題構造体
構造体

次のフィールドをもつ構造体として指定される問題構造体です。

objective — 目的関数
x0 — 出発点
Aineq — 線形不等式制約の行列
bineq — 線形不等式制約のベクトル
Aeq — 線形等式制約の行列
beq — 線形等式制約のベクトル
lb — x の下限
ub — x の上限
nonlcon — 非線形制約関数
solver — 'patternsearch'
options — optimoptions または構造体で作成されたオプション
rngstate — 乱数ジェネレータの状態をリセットするためのオプションフィールド

メモ

rngstate を除く problem 内のすべてのフィールドは必須です。

データ型: struct

出力引数

すべて折りたたむ

`x` — 解
実数ベクトル

解。実数ベクトルとして返されます。x のサイズは、x0 と同じサイズです。exitflag が正の場合、x は通常、問題に対するローカルソリューションになります。

`fval` — 解での目的関数値
実数

解での目的関数値。実数として返されます。一般的に、fval = fun(x) になります。

`exitflag` — `patternsearch` の停止理由
整数

patternsearch の停止理由。整数として返されます。

終了フラグ	意味
`1`	"非線形制約なし" — メッシュサイズの大きさが指定した許容誤差より小さく、制約違反が `ConstraintTolerance` より小さいことを示します。
`1`	"非線形制約あり" — "相補性測度" (この表の後で定義) の大きさが `sqrt(ConstraintTolerance)` より小さく、部分問題を解くのに `MeshTolerance` より細かいメッシュが使用され、制約違反が `ConstraintTolerance` より小さいことを示します。
`2`	`x` の変化とメッシュサイズがどちらも指定した許容誤差より小さく、制約違反が `ConstraintTolerance` より小さいことを示します。
`3`	`fval` の変化とメッシュサイズがどちらも指定した許容誤差より小さく、制約違反が `ConstraintTolerance` より小さいことを示します。
`4`	ステップの大きさがマシンの精度より小さく、制約違反が `ConstraintTolerance` より小さいことを示します。
`0`	関数評価または反復の最大回数に到達していることを示します。
`-1`	出力関数またはプロット関数によって最適化が停止したことを示します。
`-2`	実行可能点が検出されませんでした。

非線形制約ソルバーで、"相補性測度" は要素が c_iλ_i であるベクトルのノルムです。ここで、c_i は非線形不等式制約違反、λ_i は対応するラグランジュ乗数です。

`output` — 最適化プロセスに関する情報
構造体

最適化プロセスに関する情報。次のフィールドをもつ構造体として返されます。

function — 目的関数。
problemtype — 問題の種類。次のいずれかです:
- 'unconstrained'
- 'boundconstraints'
- 'linearconstraints'
- 'nonlinearconstr'
pollmethod — ポーリング技術。
searchmethod — 使用された検索手法（ある場合）。
iterations — 合計反復回数。
funccount — 関数評価の合計回数。
meshsize — x でのメッシュサイズ。
maxconstraint — 最大制約違反（ある場合）。
rngstate — アルゴリズムが開始する直前の MATLAB 乱数ジェネレーターの状態。ランダム検索方式またはランダムポーリング方式を使用する場合、rngstate の値を使用して出力を再現できます。ga に対する同一の手法について説明している結果を再現するを参照してください。
message — アルゴリズムが終了した理由。

アルゴリズム

デフォルトでは、線形制約がない場合、patternsearch は座標方向に沿った適応メッシュに基づいて最小値を探します。ダイレクト検索とは何ですか?およびパターン検索ポーリングの仕組みを参照してください。

Algorithm オプションを "nups" またはそのバリエーションのいずれかに設定すると、 patternsearch は非一様パターン検索 (NUPS) アルゴリズムで説明されているアルゴリズムを使用します。このアルゴリズムは、設定できるオプションが少ないなど、いくつかの点でデフォルトのアルゴリズムと異なります。

代替機能

アプリ

[最適化] ライブエディタータスクが patternsearch にビジュアルインターフェイスを提供します。

参照

[1] Audet, Charles, and J. E. Dennis Jr. “Analysis of Generalized Pattern Searches.” SIAM Journal on Optimization. Volume 13, Number 3, 2003, pp. 889–903.

[2] Conn, A. R., N. I. M. Gould, and Ph. L. Toint. “A Globally Convergent Augmented Lagrangian Barrier Algorithm for Optimization with General Inequality Constraints and Simple Bounds.” Mathematics of Computation. Volume 66, Number 217, 1997, pp. 261–288.

[3] Abramson, Mark A. Pattern Search Filter Algorithms for Mixed Variable General Constrained Optimization Problems. Ph.D. Thesis, Department of Computational and Applied Mathematics, Rice University, August 2002.

[4] Abramson, Mark A., Charles Audet, J. E. Dennis, Jr., and Sebastien Le Digabel. “ORTHOMADS: A deterministic MADS instance with orthogonal directions.” SIAM Journal on Optimization. Volume 20, Number 2, 2009, pp. 948–966.

[5] Kolda, Tamara G., Robert Michael Lewis, and Virginia Torczon. “Optimization by direct search: new perspectives on some classical and modern methods.” SIAM Review. Volume 45, Issue 3, 2003, pp. 385–482.

[6] Kolda, Tamara G., Robert Michael Lewis, and Virginia Torczon. “A generating set direct search augmented Lagrangian algorithm for optimization with a combination of general and linear constraints.” Technical Report SAND2006-5315, Sandia National Laboratories, August 2006.

[7] Lewis, Robert Michael, Anne Shepherd, and Virginia Torczon. “Implementing generating set search methods for linearly constrained minimization.” SIAM Journal on Scientific Computing. Volume 29, Issue 6, 2007, pp. 2507–2530.

拡張機能

自動並列サポート
Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

並列実行するには、'UseParallel' オプションを true に設定します。

options = optimoptions('solvername','UseParallel',true)

詳細については、Global Optimization Toolbox で並列処理を使用する方法を参照してください。

バージョン履歴

R2006a より前に導入

参考

ga | optimoptions | paretosearch | 最適化

オプション	説明	値
`Algorithm`	`patternsearch` が使用するアルゴリズム。`Algorithm` 設定は利用可能なオプションに影響します。アルゴリズムの詳細については、パターン検索ポーリングの仕組みおよび非一様パターン検索 (NUPS) アルゴリズムを参照してください。アルゴリズムの効果の例については、patternsearch アルゴリズムを調べるとライブエディタータスクの最適化における patternsearch アルゴリズムの調査を参照してください。	`{"classic"}` \| `"nups"` \| `"nups-gps"` \| `"nups-mads"`
Cache	`Cache` を `"on"` に設定すると、`patternsearch` はポーリングするメッシュポイントの履歴を保持します。後続の反復では、`patternsearch` はすでにポーリングされたポイントに近いポイントをポーリングしません。目的関数の計算中に `patternsearch` の実行速度が遅い場合は、このオプションを使用します。目的関数が確率的である場合は、このオプションを使用しないでください。メモ `Cache` は、ソルバーを並列で実行すると機能しません。	`"on"` \| `{"off"}`
CacheSize	履歴のサイズ。	非負のスカラー \| `{1e4}`
CacheTol	`patternsearch` が現在のポイントをポーリングしないようにするための、現在のメッシュポイントから履歴内の任意のポイントまでの最大距離。`Cache` オプションが `"on"` に設定されている場合に使用します。	非負のスカラー \| `{eps}`
`ConstraintTolerance`	制約に対する許容度。オプション構造の場合は、`TolCon` を使用します。	正のスカラー \| `{1e-6}`
`Display`	表示レベル。つまり、解決プロセス中に `patternsearch` がコマンドラインに返す情報の量です。	`"off"` \| `"iter"` \| `"diagnose"` \| `{"final"}`
`FunctionTolerance`	関数の許容範囲。関数値の変化が `FunctionTolerance` 未満で、メッシュサイズが `StepTolerance` 未満の場合、反復は停止します。このオプションは、MADS (メッシュアダプティブダイレクトサーチ) ポーリングには適用されません。オプション構造の場合は、`TolFun` を使用します。	非負のスカラー \| `{1e-6}`
`InitialMeshSize`	アルゴリズムの初期メッシュサイズ。パターン検索ポーリングの仕組みを参照してください。	正のスカラー \| `{1.0}`
InitialPenalty	ペナルティパラメータの初期値。パターン探索のための非線形制約ソルバーアルゴリズムを参照してください。	正のスカラー \| `{10}`
`MaxFunctionEvaluations`	目的関数評価の最大数。オプション構造の場合は、`MaxFunEvals` を使用します。	非負整数 \| `{"2000*numberOfVariables"}`、`numberOfVariables`は問題変数の数
`MaxIterations`	反復最大回数オプション構造の場合は、`MaxIter` を使用します。	非負整数 \| `{"100*numberOfVariables"}`、`numberOfVariables`は問題変数の数
MaxMeshSize	ポーリングまたは検索ステップで使用される最大メッシュサイズ。パターン検索ポーリングの仕組みを参照してください。	非負のスカラー \| `{Inf}`
`MaxTime`	最適化に許可される合計時間 (秒単位)。オプション構造の場合は、`TimeLimit` を使用します。	非負のスカラー \| `{Inf}`
`MeshContractionFactor`	失敗した反復のメッシュ収縮係数。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。オプション構造の場合は、`MeshContraction` を使用します。	正のスカラー \| `{0.5}`
`MeshExpansionFactor`	反復を成功させるためのメッシュ拡張係数。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。オプション構造の場合は、`MeshExpansion` を使用します。	正のスカラー \| `{2.0}`
MeshRotate	ポイントが最適であると宣言する前にパターンを回転させるフラグ。メッシュオプションを参照してください。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。	`"off"` \| `{"on"}`
`MeshTolerance`	メッシュサイズの許容範囲。オプション構造の場合は、`TolMesh` を使用します。	非負のスカラー \| `{1e-6}`
`OutputFcn`	各反復で最適化関数によって呼び出される関数。関数ハンドルまたは関数ハンドルのセル配列として指定します。オプション構造の場合は、`OutputFcns` を使用します。	関数ハンドルまたは関数ハンドルのセル配列 \| `{[]}`
PenaltyFactor	ペナルティ更新パラメータ。パターン探索のための非線形制約ソルバーアルゴリズムを参照してください。	正のスカラー \| `{100}`
`PlotFcn`	パターン検索からの出力のプロット。組み込みプロット関数の名前、関数ハンドル、または組み込みプロット関数または関数ハンドルの名前のセル配列として指定します。オプション構造の場合は、`PlotFcns` を使用します。	`{[]}` \| `"psplotbestf"` \| `"psplotfuncount"` \| `"psplotmeshsize"` \| `"psplotbestx"` \| `"psplotmaxconstr"` \| カスタムプロット関数
PlotInterval	プロットの反復回数。`1` は反復ごとにプロットすることを意味し、`2` は 1 回おきの反復ごとにプロットすることを意味します。	正の整数 \| `{1}`
`PollMethod`	パターン検索で使用されるポーリング戦略。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。メモ問題に線形等式制約がある場合は、MADS ポーリングは使用できません。	`{"GPSPositiveBasis2N"}` `\|` `"GPSPositiveBasisNp1"` `\|` `"GSSPositiveBasis2N"` `\|` `"GSSPositiveBasisNp1"` `\|` `"MADSPositiveBasis2N"` `\|` `"MADSPositiveBasisNp1"`
`PollOrderAlgorithm`	パターン検索におけるポーリング方向の順序。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。オプション構造の場合は、`PollingOrder` を使用します。	`"Random"` \| `"Success"` \| `{"Consecutive"}`
`ScaleMesh`	変数の自動スケーリング。オプション構造の場合は、`ScaleMesh` = `"on"` または `"off"` を使用します。	`{true}`\| `false`
`SearchFcn`	パターン検索で使用される検索のタイプ。名前または関数ハンドルとして指定します。オプション構造の場合は、`SearchMethod` を使用します。	`"GPSPositiveBasis2N" \| "GPSPositiveBasisNp1" \| "GSSPositiveBasis2N" \| "GSSPositiveBasisNp1" \| "MADSPositiveBasis2N" \| "MADSPositiveBasisNp1" \| "searchga" \| "searchlhs" \| "searchneldermead" \| "rbfsurrogate" \| {[]} \|` カスタム検索機能
`StepTolerance`	変数の許容範囲。位置の変化とメッシュサイズの両方が `StepTolerance` 未満の場合、反復は停止します。このオプションはMADSポーリングには適用されません。オプション構造の場合は、`TolX` を使用します。	非負のスカラー \| `{1e-6}`
TolBind	バインディング許容度。制約パラメータを参照してください。	非負のスカラー \| `{1e-3}`
`UseCompletePoll`	現在のポイントの周りの投票を完了するためのフラグ。パターン検索ポーリングの仕組みを参照してください。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。メモ `"classic"` アルゴリズムの場合、ベクトル化または並列ポーリングのために `UseCompletePoll` を `true` に設定する必要があります。同様に、ベクトル化または並列検索の場合は `UseCompleteSearch` を `true` に設定します。 R2019a 以降では、`UseParallel` オプションを `true` に設定すると、`patternsearch` が内部的に `UseCompletePoll` 設定を `true` にオーバーライドし、関数が並列にポーリングするようになります。オプション構造の場合は、`CompletePoll` = `"on"` または `"off"` を使用します。	`true` \| `{false}`
`UseCompleteSearch`	検索方法がポーリング方式の場合に、現在のポイントの周囲での検索を完了するためのフラグ。検索と投票を参照してください。このオプションは、`Algorithm` が `"classic"` の場合にのみ適用されます。メモ `"classic"` アルゴリズムの場合、ベクトル化または並列検索のために `UseCompleteSearch` を `true` に設定する必要があります。オプション構造の場合は、`CompleteSearch` = `"on"` または `"off"` を使用します。	`true` \| `{false}`
`UseParallel`	目的関数と非線形制約関数を並列に計算するためのフラグ。ベクトル化と並列化のオプションおよびGlobal Optimization Toolbox で並列処理を使用する方法を参照してください。メモ `"classic"` アルゴリズムの場合、ベクトル化または並列ポーリングのために `UseCompletePoll` を `true` に設定する必要があります。同様に、ベクトル化または並列検索の場合は `UseCompleteSearch` を `true` に設定します。 R2019a 以降では、`UseParallel` オプションを `true` に設定すると、`patternsearch` が内部的に `UseCompletePoll` 設定を `true` にオーバーライドし、関数が並列にポーリングするようになります。メモ `Cache` は、ソルバーを並列で実行すると機能しません。	`true` \| `{false}`
`UseVectorized`	関数がベクトル化されるかどうかを指定します。ベクトル化と並列化のオプションおよび目的関数と制約関数をベクトル化するを参照してください。メモ `"classic"` アルゴリズムの場合、ベクトル化または並列ポーリングのために `UseCompletePoll` を `true` に設定する必要があります。同様に、ベクトル化または並列検索の場合は `UseCompleteSearch` を `true` に設定します。オプション構造の場合は、`Vectorized` = `"on"` または `"off"` を使用します。	`true` \| `{false}`

patternsearch

構文

説明

例

制約なしパターン探索最小化

線形不等式制約によるパターン検索

境界付きパターン検索

非線形制約によるパターン検索

さまざまなpatternsearchアルゴリズムを試す

デフォルト以外のオプションを使用したパターン検索

関数値と最小点を取得する

すべての出力の取得

入力引数

fun — 最小化される機能 関数ハンドル | 関数名

x0 — 初期点 実数ベクトル

A — 線形不等式制約 実数行列

b — 線形不等式制約 実数ベクトル

Aeq — 線形等式制約 実数行列

beq — 線形等式制約 実数ベクトル

lb — 下限 実数ベクトル | 実数配列

ub — 上限 実数ベクトル | 実数配列

nonlcon — 非線形制約 関数ハンドル | 関数名

options — 最適化オプション optimoptions によって返されるオブジェクト | 構造体

problem — 問題構造体 構造体

出力引数

x — 解 実数ベクトル

fval — 解での目的関数値 実数

exitflag — patternsearch の停止理由 整数

output — 最適化プロセスに関する情報 構造体

アルゴリズム

代替機能

アプリ

参照

拡張機能

自動並列サポート Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

バージョン履歴

参考

トピック

さまざまな`patternsearch`アルゴリズムを試す

`fun` — 最小化される機能
関数ハンドル | 関数名

`x0` — 初期点
実数ベクトル

`A` — 線形不等式制約
実数行列

`b` — 線形不等式制約
実数ベクトル

`Aeq` — 線形等式制約
実数行列

`beq` — 線形等式制約
実数ベクトル

`lb` — 下限
実数ベクトル | 実数配列

`ub` — 上限
実数ベクトル | 実数配列

`nonlcon` — 非線形制約
関数ハンドル | 関数名

`options` — 最適化オプション
`optimoptions` によって返されるオブジェクト | 構造体

`problem` — 問題構造体
構造体

`x` — 解
実数ベクトル

`fval` — 解での目的関数値
実数

`exitflag` — `patternsearch` の停止理由
整数

`output` — 最適化プロセスに関する情報
構造体

自動並列サポート
Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。