このページは機械翻訳を使用して翻訳されました。元の英語を参照するには、ここをクリックします。

`patternsearch` アルゴリズムを調べる

R2022b 以降、patternsearch には 4 つのアルゴリズムがあります。

"classic"
"nups" (非均一パターン検索)
"nups-gps"
"nups-mads"

この例では、アルゴリズムの選択が、滑らかでない目的関数を持つ境界付き問題にどのように影響するかを示します。

目的関数

この例の目的関数は、例を実行するときに使用できる 2 次元 ps_example 関数に基づいています。

type ps_example

function f = ps_example(x)
%PS_EXAMPLE objective function for patternsearch.

%   Copyright 2003-2021 The MathWorks, Inc.

f = zeros(1,size(x,1));
for i = 1:size(x,1)
    if  x(i,1) < -5
        f(i) = (x(i,1)+5)^2 + abs(x(i,2));
    elseif x(i,1) < -3
        f(i) = -2*sin(x(i,1)) + abs(x(i,2));
    elseif x(i,1) < 0
        f(i) = 0.5*x(i,1) + 2 + abs(x(i,2));
    elseif x(i,1) >= 0
        f(i) = .3*sqrt(x(i,1)) + 5/2 +abs(x(i,2));
    end
end

2 つの次元ごとに原点からの疑似ランダムオフセットを作成し、結果の目的を追加することで、ps_example 関数を任意の偶数次元に拡張します。この例の最後にある testps ヘルパー関数のコードをご覧ください。

N = 10 次元を指定し、各コンポーネントの境界を -20 ～ 20 に設定します。x0 = [0 0 ... 0] の地点から patternsearch を開始します。

N = 10;
lb = -20*ones(1,N);
ub = -lb;
x0 = zeros(size(lb));

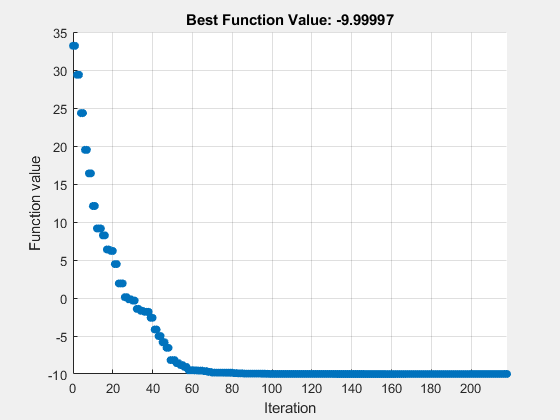
クラシックアルゴリズムを実行する

"classic" アルゴリズムを使用し、目的関数の値を表示するためのオプションを設定します。

optscl = optimoptions("patternsearch",Algorithm="classic",PlotFcn="psplotbestf");

最適化を実行します。

[xclassic,fvalclassic,eflagclassic,outputclassic] = ...
    patternsearch(@testps,x0,[],[],[],[],lb,ub,[],optscl)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

xclassic = 1×10

   -7.9575    5.9058   -8.5047   -5.5481   -8.9402   -2.8633   -7.5058    0.8919   -5.6967    2.9322

fvalclassic = -10.0000

eflagclassic = 1

outputclassic = struct with fields:
         function: @testps
      problemtype: 'boundconstraints'
       pollmethod: 'gpspositivebasis2n'
    maxconstraint: 0
     searchmethod: []
       iterations: 218
        funccount: 3487
         meshsize: 9.5367e-07
         rngstate: [1x1 struct]
          message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'

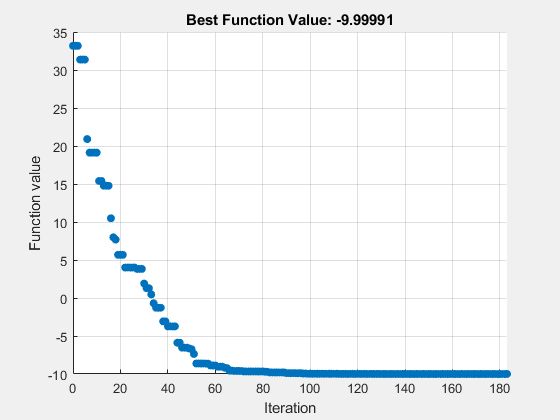
NUPSアルゴリズムを実行する

"nups" アルゴリズムを使用するためのオプションを設定します。再現可能な結果を得るには、ランダムシードを設定します。

optsnups = optimoptions(optscl,Algorithm="nups");
rng default % For reproducibility
[xnups,fvalnups,eflagnups,outputnups] = ...
    patternsearch(@testps,x0,[],[],[],[],lb,ub,[],optsnups)

patternsearch stopped because the mesh size was less than options.MeshTolerance.

xnups = 1×10

   -7.9575    5.9058   -8.5047   -5.5480   -8.9401   -2.8633   -7.5058    0.8919   -5.6967    2.9322

fvalnups = -9.9999

eflagnups = 1

outputnups = struct with fields:
         function: @testps
      problemtype: 'boundconstraints'
       pollmethod: 'nups'
    maxconstraint: 0
     searchmethod: []
       iterations: 183
        funccount: 1827
         meshsize: 8.5928e-07
         rngstate: [1x1 struct]
          message: 'patternsearch stopped because the mesh size was less than options.MeshTolerance.'

この場合、"nups" アルゴリズムは、より少ない関数評価を使用しながら、"classic" アルゴリズムと本質的に同じソリューションに到達します。

さらなる探究

"nups-gps" アルゴリズムと "nups-mads" アルゴリズムを試して、この問題でのパフォーマンスを確認することもできます。どのアルゴリズムが問題に対して最も効果的であるかを常に予測できるわけではありませんが、"nups" は多くの適応機能を組み込んでおり、最適なアルゴリズムである可能性が高いため、適切な開始アルゴリズムになる可能性があります。

補助関数

次のコードは、補助関数 testps を作成します。

function y = testps(x) 
    N = numel(x); % Number of variables
    if mod(N,2) == 1
        disp("Number of variables must be even.")
        return
    end
    strm = RandStream("twister",Seed=1); % Set Seed for consistency
    % Use RandStream to avoid affecting the global stream
    dsp = 5*randn(strm,size(x));
    z = x - dsp; % Include random offsets
    y = 0;
    for i = 1:N/2
        y = y + ps_example(z([2*i-1,2*i]));
    end
end

参考

patternsearch

patternsearch アルゴリズムを調べる