パターン探索ポーリングの仕組み

このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

パターン探索ポーリングの仕組み

コンテキスト

patternsearch は、最適点に近づく一連の点、x0、x1、x2、... を見つけます。目的関数の値は、シーケンス内の各ポイントから次のポイントにかけて減少するか、同じままになります。このセクションでは、GPSアルゴリズムを使用した最適化で説明されている関数のパターン探索がどのように機能するかについて説明します。

説明を簡略化するために、このセクションでは、デフォルトの最大正基底 2 N を使用し、ScaleMesh オプションを false に設定して、一般化パターン探索(GPS) がどのように機能するかについて説明します。

このセクションでは、patternsearch アルゴリズムが境界または線形制約でどのように機能するかについては説明しません。境界と線形制約の場合、patternsearch は、すべての境界と線形制約を満たすように、ポール点を反復ごとに実行可能になるように変更します。

このセクションでは非線形制約は扱いません。patternsearch が非線形制約でどのように動作するかを理解するには、パターン探索のための非線形制約ソルバーアルゴリズムを参照してください。

成功したポーリング

パターン探索は、指定した初期点 x0 から始まります。この例では、x0 = [2.1 1.7] となります。

反復1

最初の反復では、メッシュサイズは 1 で、GPS アルゴリズムはパターンベクトルを初期点 x0 = [2.1 1.7] に追加して、次のメッシュポイントを計算します。

[1 0] + x0 = [3.1 1.7]
[0 1] + x0 = [2.1 2.7]
[-1 0] + x0 = [1.1 1.7]
[0 -1] + x0 = [2.1 0.7]

アルゴリズムは、上記に示した順序でメッシュポイントで目的関数を計算します。次の図は、初期点とメッシュポイントにおける目的関数の値を示しています。

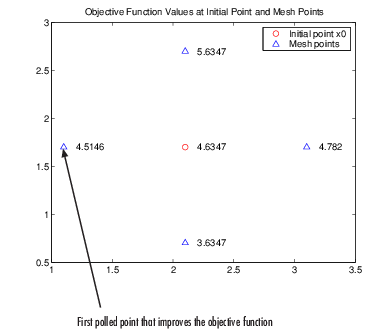
アルゴリズムは、メッシュポイントの目的関数値を計算して、その値が x0 の値である 4.6347 より小さいメッシュポイントを見つけるまでメッシュポイントをポーリングします。この場合、最初に見つかるポイントは [1.1 1.7] であり、目的関数の値は 4.5146 なので、反復 1 でのポーリングは成功となります。アルゴリズムは、シーケンスの次の点を次の値に設定します。

x1 = [1.1 1.7]

メモ

デフォルトでは、GPSパターン探索アルゴリズムは、現在のポイントよりも適応値が小さいメッシュポイントを見つけるとすぐに、現在の反復を停止します。その結果、アルゴリズムはすべてのメッシュポイントをポーリングしない可能性があります。UseCompletePoll オプションを true に設定すると、アルゴリズムですべてのメッシュポイントをポーリングできます。

反復2

ポーリングが成功すると、アルゴリズムは現在のメッシュサイズを MeshExpansionFactor オプションのデフォルト値である 2 で乗算します。初期メッシュサイズは 1 なので、2 回目の反復ではメッシュサイズは 2 になります。反復 2 のメッシュには次の点が含まれます。

2*[1 0] + x1 = [3.1 1.7]
2*[0 1] + x1 = [1.1 3.7]
2*[-1 0] + x1 = [-0.9 1.7]
2*[0 -1] + x1 = [1.1 -0.3]

次の図は、ポイント x1 とメッシュポイント、および対応する目的関数の値を示しています。

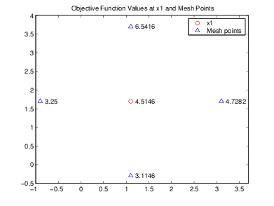
アルゴリズムは、値が 4.5146 (x1 の値) より小さいメッシュポイントが見つかるまでメッシュポイントをポーリングします。最初に見つかったポイントは [-0.9 1.7] であり、ここで目的関数の値は 3.25 なので、反復 2 でのポーリングは再び成功します。アルゴリズムは、シーケンスの2番目のポイントを次のように設定します。

x2 = [-0.9 1.7]

ポーリングが成功したため、アルゴリズムは現在のメッシュサイズを 2 倍にして、3 回目の反復でメッシュサイズを 4 にします。

失敗した世論調査

4回目の反復で、現在のポイントは

x3 = [-4.9 1.7]

メッシュサイズは8なので、メッシュは点から構成されます

8*[1 0] + x3 = [3.1 1.7]
8*[0 1] + x3 = [-4.9 9.7]
8*[-1 0] + x3 = [-12.9 1.7]
8*[0 -1] + x3 = [-4.9 -1.3]

次の図は、メッシュポイントとその目的関数の値を示しています。

この反復では、どのメッシュポイントも x3 の値よりも小さい目的関数値を持たないため、ポーリングは失敗となります。この場合、アルゴリズムは次の反復で現在のポイントを変更しません。つまり、

x4 = x3;

次の反復では、アルゴリズムは現在のメッシュサイズに 0.5 (MeshContractionFactor オプションの既定値) を掛けて、次の反復でのメッシュサイズが 4 になるようにします。次に、アルゴリズムはより小さなメッシュサイズでポーリングを行います。

MADSにおける成功と失敗のポーリング

PollMethod オプションを 'MADSPositiveBasis2N' または 'MADSPositiveBasisNp1' に設定すると、patternsearch は異なるポーリングタイプを使用するようになり、他のポーリングアルゴリズムとは異なる方法でポーリングに反応するようになります。

MADS ポーリングでは、各反復で新しく生成された疑似ランダムメッシュベクトルが使用されます。ベクトルは、ランダムな下三角行列の列からランダムにシャッフルされた要素です。行列の要素は 1/ $\sqrt{mesh size}$ までの整数サイズを持ちます。ポーリングでは、メッシュベクトルはメッシュサイズで乗算されるため、ポール点は現在のポイントから最大 $\sqrt{mesh size}$ になります。

失敗したポーリングでは、MeshContractionFactor オプションを無視して、メッシュが 4 倍に縮小されます。同様に、ポーリングが成功すると、MeshExpansionFactor オプションは無視され、メッシュが 4 倍に拡張されます。MaxMeshSize オプションの設定に関係なく、最大メッシュサイズは 1 です。

さらに、ポーリングが成功した場合、patternsearch は成功したポイントから開始して再度ポーリングを実行します。この追加のポーリングでは、サイズ 1 未満のまま、係数 4 で拡張された同じメッシュベクトルが使用されます。追加の世論調査では、先ほど成功したのと同じ方向を再度調べます。

各反復での結果の表示

Display オプションを 'iter' に設定すると、各反復でのパターン探索の結果を表示できます。これにより、パターン探索の進行状況を評価し、必要に応じて options に変更を加えることができます。

この設定では、パターン探索コマンドラインに各反復に関する情報が表示されます。最初の4つの反復は

Iter     f-count          f(x)      MeshSize     Method
    0        1        4.63474             1      
    1        4        4.51464             2     Successful Poll
    2        7           3.25             4     Successful Poll
    3       10      -0.264905             8     Successful Poll
    4       14      -0.264905             4     Refine Mesh

Method の下のエントリ Successful Poll は、現在の反復が成功したことを示します。たとえば、反復 2 でのポーリングは成功します。その結果、f(x) の下に表示される反復 2 で計算されたポイントの目的関数の値は、反復 1 の値よりも小さくなります。

反復 4 では、エントリ Refine Mesh によって、ポーリングが失敗したことが示されます。その結果、反復 4 での関数値は反復 3 から変更されません。

デフォルトでは、パターン探索は、ポーリングが成功するたびにメッシュサイズを 2 倍にし、ポーリングが失敗するたびにメッシュサイズを半分にします。

さらなる反復

パターン探索は停止する前に 60 回の反復を実行します。次のプロットは、パターン探索の最初の 13 回の反復で計算されたシーケンス内のポイントを示しています。

ポイントの下の数字は、アルゴリズムがポイントを見つける最初の反復を示します。ポーリングが失敗した後も最良のポイントは変わらないため、プロットには成功したポーリングに対応する反復回数のみが表示されます。たとえば、反復 4 および 5 での最適なポイントは、反復 3 での最適なポイントと同じです。

ポーリング方法

各反復で、パターン探索は現在のメッシュ内のポイントをポーリングします。つまり、メッシュポイントで目的関数を計算し、関数値が現在のポイントの関数値よりも小さい関数があるかどうかを確認します。パターン探索ポーリングの仕組みはポーリングの例を示しています。PollMethod オプションでメッシュを定義するパターンを指定できます。デフォルトのパターン 'GPSPositiveBasis2N' は、次の 2 つの N 方向で構成されます。ここで、N は目的関数の独立変数の数です。

[1 0 0...0]
[0 1 0...0]
...
[0 0 0...1]
[–1 0 0...0]
[0 –1 0...0]
[0 0 0...–1].

たとえば、目的関数に 3 つの独立変数がある場合、GPS Positive basis 2N は次の 6 つのベクトルで構成されます。

[1 0 0]
[0 1 0]
[0 0 1]
[–1 0 0]
[0 –1 0]
[0 0 –1]。

あるいは、PollMethod オプションを 'GPSPositiveBasisNp1' に設定して、次の N + 1 方向で構成されるパターンを設定することもできます。

[1 0 0...0]
[0 1 0...0]
...
[0 0 0...1]
[–1 –1 –1...–1].

たとえば、目的関数に 3 つの独立変数がある場合、'GPSPositiveBasisNp1' は次の 4 つのベクトルで構成されます。

[1 0 0]
[0 1 0]
[0 0 1]
[–1 –1 –1]。

パターン探索では、PollMethod として 'GPSPositiveBasis2N' を使用するよりも 'GPSPositiveBasisNp1' を使用した方が、アルゴリズムが各反復で探索するポイントが少なくなるため、実行速度が速くなることがあります。この例では説明されていませんが、'MADSPositiveBasis2N' ではなく 'MADSPositiveBasisNp1' を使用する場合も同じことが当てはまり、GSS でも同様です。たとえば、patternsearch と Optimize ライブエディタータスクを使用した制約付き最小化の線形制約の例でパターン探索を実行すると、アルゴリズムは 'GPSPositiveBasis2N' (デフォルトの PollMethod) を使用して 1588 回の関数評価を実行しますが、'GPSPositiveBasisNp1' を使用した場合は 877 回の関数評価しか実行しません。詳細については、patternsearch を用いた大域的最小値の探索を参照してください。

ただし、目的関数に多くの局所的最小値がある場合、'GPSPositiveBasis2N' を PollMethod として使用すると、各反復で現在のポイントの周囲のより多くのポイントが探索されるため、大域的最小値ではない局所的最小値を見つけることを回避できる可能性があります。

ポーリングを完了する

デフォルトでは、パターン探索によって目的関数の値を改善するメッシュポイントが見つかった場合、ポーリングが停止され、そのポイントが次の反復の現在のポイントとして設定されます。この問題が発生すると、一部のメッシュポイントがポーリングされない可能性があります。これらのポーリングされていないポイントの一部は、パターン探索で最初に見つかった目的関数の値よりもさらに低い目的関数の値を持つ可能性があります。

複数の局所最小値がある問題の場合、パターン探索で各反復でメッシュポイントを すべて ポーリングし、最適な目的関数値を持つものを選択することが望ましい場合があります。これにより、パターン探索では各反復でより多くのポイントを探索できるようになり、大域的最小値ではない局所的最小値を回避できる可能性があります。パターン探索でメッシュ全体をポーリングし、UseCompletePoll オプションを true に設定します。

パターン探索の停止条件

次のいずれかの条件が発生すると、アルゴリズムは停止します。

メッシュサイズは MeshTolerance オプションよりも小さくなります。
アルゴリズムによって実行される反復回数が、MaxIterations オプションの値に達します。
アルゴリズムによって実行される目的関数評価の合計数が、MaxFunctionEvaluations オプションの値に達します。
MaxTime オプションの値に達するまでアルゴリズムが実行される時間 (秒)。
ポーリングが成功すると、前の 2 回の反復で見つかったポイント間の距離とメッシュサイズは両方とも StepTolerance オプションよりも小さくなります。
ポーリングが成功すると、前の 2 回の反復における目的関数の変化は FunctionTolerance オプションよりも小さくなり、メッシュサイズは StepTolerance オプションよりも小さくなります。

ConstraintTolerance オプションは停止基準として使用されません。非線形制約に関する実現可能性を決定します。

MADS アルゴリズムは、メッシュサイズ停止基準で、ポールパラメーターΔ_p と呼ばれる追加のパラメーターを使用します。

$Δ_{p} = {\begin{array}{l} N \sqrt{Δ_{m}} & for positive basis N + 1 poll \\ \sqrt{Δ_{m}} & for positive basis 2 N poll, \end{array}$

ここでΔ_mはメッシュサイズです。MADS 停止基準は次のとおりです。

Δ_p ≤ MeshTolerance.

パターン探索の堅牢性

パターン探索アルゴリズムは、目的関数の障害に対して堅牢です。つまり、patternsearch は、NaN、Inf、または複素数値をもたらす関数評価を許容します。初期点 x0 の目的関数が実数の有限値である場合、patternsearch はポール点の失敗を目的関数の値が大きいものとして扱い、無視します。

たとえば、ポーリング内のすべてのポイントが NaN と評価された場合、patternsearch はポーリングが失敗したと見なし、メッシュを縮小して再評価します。ポーリング内の 1 つのポイントでも、これまでのどのポイントよりも小さい値と評価された場合、patternsearch はポーリングが成功したと見なし、メッシュを拡張します。