このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

一般化パターン探索における完全ポーリングの使用

R2025a

次の関数を考えてみましょう。

$f (x_{1}, x_{2}) = {\begin{array}{l} x_{1}^{2} + x_{2}^{2} - 25 & for x_{1}^{2} + x_{2}^{2} \leq 25 \\ x_{1}^{2} + {(x_{2} - 9)}^{2} - 16 & for x_{1}^{2} + {(x_{2} - 9)}^{2} \leq 16 \\ 0 & otherwise . \end{array}$

次の図は関数のプロットを示しています。

図を生成するコード

[X,Y] = meshgrid(-6:.1:6,-6:.1:14);
Z = zeros(size(X));
for i = 1:size(X,1)
for j=1:size(X,2)
Z(i,j) = poll_example([X(i,j),Y(i,j)]);
end;end;
surf(X,Y,Z,'LineStyle','none');
view([-60,30])
annotation('textarrow',[0.24 0.38],...
    [0.11 0.47],'String',{'Local minimum at [0,9]'});
annotation('textarrow',[0.68 0.6],...
    [0.15 0.26],'String',{'Global minimum at [0,0]'});

関数の大域的最小値は (0, 0) で発生し、その値は -25 です。ただし、この関数は (0, 9) でも局所的最小値を持ち、その値は -16 になります。

関数を計算するファイルを作成するには、次のコードをコピーして、MATLAB^® エディターの新しいファイルに貼り付けます。

function z = poll_example(x)
if x(1)^2 + x(2)^2 <= 25
    z = x(1)^2 + x(2)^2 - 25;
elseif x(1)^2 + (x(2) - 9)^2 <= 16
    z = x(1)^2 + (x(2) - 9)^2 - 16;
else z = 0;
end
end

MATLAB パス上のフォルダーにファイル名を poll_example.m としてファイルを保存します。

関数に対してパターン探索を実行するには、次のように入力します。

options = optimoptions('patternsearch','Display','iter');
[x,fval] = patternsearch(@poll_example,[0,5],...
    [],[],[],[],[],[],[],options)

MATLAB は反復と解のテーブルを返します。

x =

     0     9


fval =

   -16

アルゴリズムは、初期点 f(0, 5) = 0. で関数を評価することから始まります。ポーリングでは、最初の反復中に次のものが評価されます。

f((0, 5) + (1, 0)) = f(1, 5) = 0

(1)

f((0, 5) + (0, 1)) = f(0, 6) = -7

(2)

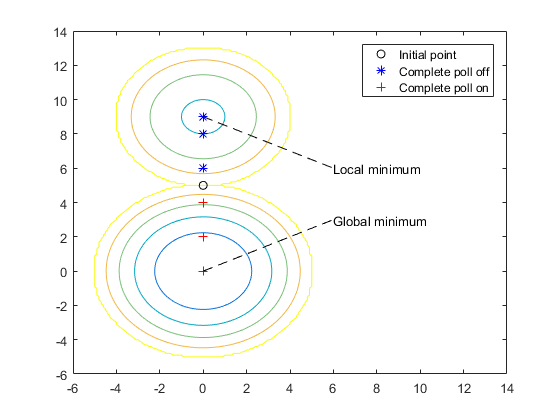
探索は、目的関数の値が初期点よりも小さいメッシュポイント (0, 6) をポーリングするとすぐに、現在のメッシュのポーリングを停止し、次の反復で現在のポイントを (0, 6) に設定します。その結果、最初の反復では、探索は（0、9）の局所的最小値に向かって移動します。これは、コマンドライン表示の最初の 2 行を見るとわかります。

Iter     f-count     f(x)      MeshSize     Method
    0        1         0             1      
    1        3        -7             2     Successful Poll

パターン探索では、最初の反復で目的関数の評価が 2 回のみ実行されるため、関数の合計数が 1 から 3 に増加することに注意してください。

次に、UseCompletePoll を true に設定して最適化を再実行します。

options.UseCompletePoll = true;
[x,fval] = patternsearch(@poll_example,[0,5],...
    [],[],[],[],[],[],[],options);

今回は、パターン探索(0, 0) で大域的最小値が見つかります。この実行と前回の実行の違いは、UseCompletePoll が true に設定されている場合、最初の反復でパターン探索が4 つのメッシュポイントすべてをポーリングすることです。

f((0, 5) + (1, 0)) = f(1, 5) = 0

(3)

f((0, 5) + (0, 1)) = f(0, 6) = -6

(4)

f((0, 5) + (-1, 0)) = f(-1, 5) = 0

(5)

f((0, 5) + (0, -1)) = f(0, 4) = -9

(6)

最後のメッシュポイントは目的関数の値が最も低いため、パターン探索では次の反復でそのポイントが現在のポイントとして選択されます。コマンドライン表示の最初の 2 行にこれが表示されます。

Iter     f-count     f(x)      MeshSize     Method
    0        1         0             1      
    1        5        -9             2     Successful Poll

この場合、目的関数は最初の反復で 4 回評価されます。その結果、パターン探索は(0, 0) の大域的最小値に向かって移動します。

次の図は、完全なポーリング が Off に設定されている場合に返されるポイントのシーケンスと、完全なポーリング が On の場合に返されるポイントのシーケンスを比較しています。

図を生成するコード

function graph_poll_example

[X,Y] = meshgrid(-6:.1:14,-6:.1:14);
Z = zeros(size(X));
for i = 1:size(X,1)
    for j=1:size(X,2)
        Z(i,j) = poll_example([X(i,j),Y(i,j)]);
    end;
end;
contour(X,Y,Z);
hold on

h = plot(0,5,'ko');

opts = optimoptions('patternsearch','OutputFcn',@plotpnt,'UseCompletePoll',false);
[thex,thefv] = patternsearch(@poll_example,[0,5],...
    [],[],[],[],[],[],[],opts);

opts = optimoptions('patternsearch','OutputFcn',@plotpnt,'UseCompletePoll',true);
[thex,thefv] = patternsearch(@poll_example,[0,5],...
    [],[],[],[],[],[],[],opts);
hold off

legend([h,ff,tt],'Initial point','Complete poll off','Complete poll on')

line([0,6],[9,6],'Color','k','LineStyle','--')
line([0,6],[0,3],'Color','k','LineStyle','--')

text(6,6,'Local minimum')
text(6,3,'Global minimum')

function [stop,opts,optchanged] = plotpnt(optimvalues,opts,flag)
    if strcmp(flag,'iter')
        if isequal(opts.UseCompletePoll,true)
            tt = plot(optimvalues.x(1),optimvalues.x(2),'r+');
        else
            ff = plot(optimvalues.x(1),optimvalues.x(2),'b*');
        end
    end
stop = false;
optchanged = false;
end

end

一般化パターン探索における完全ポーリングの使用

参考

トピック