patternsearch と Optimize を使用した制約付き最小化ライブエディタータスク - MATLAB & Simulink

このページは機械翻訳を使用して翻訳されました。元の英語を参照するには、ここをクリックします。

`patternsearch` と `Optimize` を使用した制約付き最小化ライブエディタータスク

この例では、視覚的なアプローチを提供する最適化ライブエディタータスクとコマンドラインの両方を使用して、制約付き最小化問題を解決する方法を示します。

問題の説明

この問題では、patternsearch を使用して非線形関数を最小化するときに、線形制約と非線形制約を使用します。目的関数は次のとおりです。

$F (x) = \frac{1}{2} x^{T} H x + f^{T} x,$

ここで、

H = [36 17 19 12  8 15; 
     17 33 18 11  7 14; 
     19 18 43 13  8 16;
     12 11 13 18  6 11; 
      8  7  8  6  9  8; 
     15 14 16 11  8 29];

f = [ 20 15 21 18 29 24 ]';
 
F = @(x)0.5*x'*H*x + f'*x;

線形制約は

$\begin{matrix} A \cdot x \leq b, \\ A e q \cdot x = b e q, \end{matrix}$

ここで、

A = [-8 7 3 -4 9 0];
b = 7;
Aeq = [7 1 8 3 3 3;
      5 0 -5 1 -5 8;
     -2 -6 7 1 1 9;
      1 -1 2 -2 3 -3];
beq = [84 62 65 1]';

続行する前に、前述のコードセクションを入力して、問題の変数をワークスペースに取得します。

最適化ライブエディタータスクで`patternsearch`を使用して解決する

[ホーム] タブの [ファイル] セクションで [新規ライブスクリプト] ボタンをクリックして、新しいライブスクリプトを作成します。
[最適化] ライブエディタータスクを挿入します。[挿入] タブをクリックしてから、[コード] セクションで、[タスク]、[最適化] を選択します。
この例の場合は、ソルバーベースのタスクを選択します。
問題の種類を指定
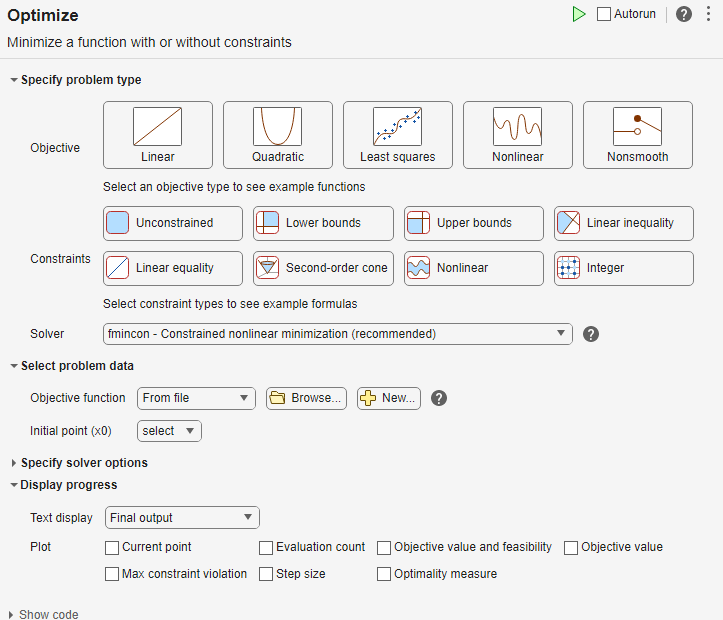
タスクの Specify problem type セクションで、Objective > Nonlinear ボタンをクリックします。
Constraints > Linear inequality ボタンと Linear equality ボタンをクリックします。
Solver > patternsearch - Pattern searchを選択します。
問題データの選択
タスクの Select problem data セクションに問題の変数を入力します。目的関数を指定するには、Objective function > Function handle を選択し、F を選択します。
不等式制約を A と b に設定します。等式制約を Aeq と beq に設定します。
初期ポイントを設定するには、まずタスクの上に新しいセクションを作成する必要があります。これを行うには、[Insert] タブの [Section Break] ボタンをクリックします。タスクの上の新しいセクションに、初期点の次のコードを入力します。
```
x0 = [2 1 0 9 1 0]';
```
セクションを実行して、x0 をワークスペースに配置します。セクションを実行するには、セクション内にカーソルを置き、Ctrl+Enter を押すか、行番号の左側にある青い縞模様のバーをクリックします。
タスクの Select problem data セクションで、x0 を初期ポイントとして設定します。
ソルバーオプションを指定する
この問題は線形制約されているため、追加のソルバーオプションを指定します。タスクの Specify solver options セクションを展開し、 Add ボタンをクリックします。Poll settings > Poll method を GSSPositiveBasis2N に設定します。線形制約問題に対する GSS ポーリング法の効率性の詳細については、投票オプションの効率を比較するを参照してください。
表示オプションを設定する
タスクの Display progress セクションで、Best value および Mesh size プロット関数を選択します。
設定は次のようになります。
ソルバーの実行と結果の検証
ソルバーを実行するには、タスクウィンドウの右上にあるオプションボタン [⁝] をクリックして、[セクションの実行] を選択します。
プロットは別の図ウィンドウとタスク出力領域に表示されます。
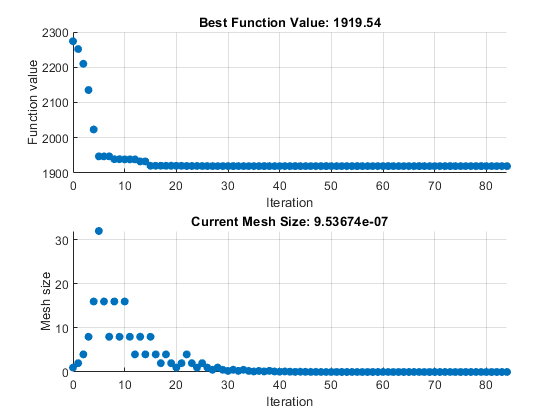
解点と解における目的関数の値を取得するには、タスクの上部を確認します。
Optimize ライブエディタータスクは、ソリューションを solution という名前の変数に返し、目的関数の値を objectiveValue という名前の変数に返します。これらの値を表示するには、タスクの下のセクションに次のコードを入力してセクションを実行するか、MATLAB^® コマンドラインでコードを入力します。
```
disp(solution)
```
```
    8.5165
   -6.1094
    4.0989
    1.2877
   -4.2348
    2.1812
```
```
disp(objectiveValue)
```
```
   1.9195e+03
```
非線形制約を含める
次の非線形制約を問題に追加します。
$\begin{matrix} - 1.5 + x_{1} x_{2} + x_{1} - x_{2} \leq 0 \\ - x_{1} x_{2} - 10 \leq 0. \end{matrix}$
これらの制約を含めるには、まず Constraints > Nonlinear ボタンをクリックします。
Select problem data セクションの Constraints の下で、Nonlinear > Local function を選択し、New ボタンをクリックします。タスクの下側の新しいセクションに関数が表示されます。結果のコードを編集して、次の行を含めます。
```
function [c, ceq] = double_ineq(x)
c = [-1.5 + x(1)*x(2) + x(1) - x(2);
    -x(1)*x(2) - 10];
ceq = [];
end
```
Nonlinear 制約セクションで、double_ineq を選択します。
非線形制約アルゴリズムにより、patternsearch は多くの関数評価を実行します。Specify solver options セクションで、現在のオプションの右側にあるプラス記号をクリックして、追加のオプションを表示します。次に、関数評価の最大制限を 5e4 に増やします。
タスクを再度実行して最適化を再実行します。

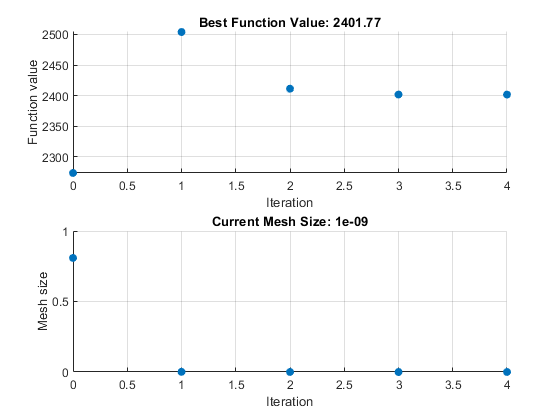
ソリューションと目的関数の値を表示します。

disp(solution)

disp(objectiveValue)

   2.4018e+03

目的関数の値は、非線形制約のない問題の値よりも高くなります。以前のソリューションは、非線形制約に関しては実行可能ではありません。

非線形制約アルゴリズムによって patternsearch アルゴリズムが変更され、修正された問題を解決するために別の外部ループが含まれるようになったため、プロットでは以前よりも反復回数が大幅に少なくなっていることがわかります。外側のループは、各主要な反復で問題に対する変更を減らします。この場合、アルゴリズムは外側の反復を 4 回だけ実行します。アルゴリズムの詳細については、パターン探索のための非線形制約ソルバーアルゴリズムを参照してください。

コマンドラインで`patternsearch`を使用して解決する

元の問題 (線形制約のみ) をコマンドラインで解決するには、次のコードを実行します。

x0 = [2 1 0 9 1 0]';
options = optimoptions('patternsearch',...
    'PollMethod','GSSPositiveBasis2N',...
    'PlotFcn',{'psplotbestf','psplotmeshsize'});
lb = [];
ub = [];
nonlcon = [];
[x,fval] = patternsearch(F,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

Optimization terminated: mesh size less than options.MeshTolerance.

x =

    8.5165
   -6.1094
    4.0989
    1.2877
   -4.2348
    2.1812


fval =

   1.9195e+03

patternsearch は、最適化ライブエディタータスクの例に示されている最初のプロットのペアを生成します。

非線形制約を含めるには、次のコードを MATLAB パス上の double_ineq.m という名前のファイルに保存します。

function [c, ceq] = double_ineq(x)
c = [-1.5 + x(1)*x(2) + x(1) - x(2);
    -x(1)*x(2) - 10];
ceq = [];
end

非線形制約付きでソルバーが完了するまで実行できるようにするには、許可される関数評価の数を増やします。

options.MaxFunctionEvaluations = 5e4;

非線形制約を含む問題を解きます。

nonlcon = @double_ineq;
[x,fval] = patternsearch(F,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

    7.2083
   -1.3873
    4.9579
   -3.1393
   -3.1843
    4.7457


fval =

   2.4018e+03

patternsearch は、最適化ライブエディタータスクの例に示されている 2 番目のプロットペアも生成します。

最適化ライブエディタータスクとコマンドラインの両方を使用して問題を定式化して解決することができ、同じ結果が得られます。コマンドラインはより合理化されていますが、ソルバーの選択、問題の設定、プロット関数などのオプションの選択に関するヘルプは少なくなっています。また、Optimize を使用して問題を開始し、[最適化] ライブエディタータスクまたはソルバーを使用した制約付き非線形問題のように、コマンドラインで使用するためのコードを生成することもできます。

参考

patternsearch