このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

パターン探索を用いた制約付き最小化、ソルバーベース

この例では、パターン探索を使用して、非線形不等式制約と境界に従って目的関数を最小化する方法を示します。この例の問題ベースのバージョンについては、パターン探索を用いた制約付き最小化、問題ベースを参照してください。

制約付き最小化問題

この問題では、最小化する目的関数は 2 次元変数 x の単純な関数です。

simple_objective(x) = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;

この機能は、L.C.W. DixonとG.P. Szego [1]によって説明されているように、「カム」として知られています。

さらに、この問題には非線形の制約と境界があります。

   x(1)*x(2) + x(1) - x(2) + 1.5 <= 0  (nonlinear constraint)
   10 - x(1)*x(2) <= 0                 (nonlinear constraint)
   0 <= x(1) <= 1                      (bound)
   0 <= x(2) <= 13                     (bound)

目的関数をコード化する

次のコードを含む simple_objective.m という名前の MATLAB ® ファイルを作成します。

type simple_objective

function y = simple_objective(x)
%SIMPLE_OBJECTIVE Objective function for PATTERNSEARCH solver

%   Copyright 2004 The MathWorks, Inc.  

x1 = x(1);
x2 = x(2);
y = (4-2.1.*x1.^2+x1.^4./3).*x1.^2+x1.*x2+(-4+4.*x2.^2).*x2.^2;

patternsearch などのソルバーは単一の入力 x を受け入れます。ここで、x には問題内の変数の数と同じ数の要素があります。目的関数は目的関数のスカラー値を計算し、それを単一の出力引数 y で返します。

制約関数のコーディング

次のコードを含む simple_constraint.m という名前の MATLAB ファイルを作成します。

type simple_constraint

function [c, ceq] = simple_constraint(x)
%SIMPLE_CONSTRAINT Nonlinear inequality constraints.

%   Copyright 2005-2007 The MathWorks, Inc.

c = [1.5 + x(1)*x(2) + x(1) - x(2); 
     -x(1)*x(2) + 10];

% No nonlinear equality constraints:
ceq = [];

制約関数は、すべての不等式制約と等式制約の値を計算し、それぞれベクトル c と ceq を返します。c の値は、ソルバーがゼロ以下にしようとする非線形不等式制約を表します。ceq の値は、ソルバーがゼロに等しくしようとする非線形等式制約を表します。この例には非線形等式制約がないため、ceq = [] となります。詳細は、非線形制約を参照してください。

patternsearchを使用して最小化

目的関数を関数ハンドルとして指定します。

ObjectiveFunction = @simple_objective;

問題の範囲を指定します。

lb = [0 0];   % Lower bounds
ub = [1 13];  % Upper bounds

非線形制約関数を関数ハンドルとして指定します。

ConstraintFunction = @simple_constraint;

ソルバーの初期点を指定します。

x0 = [0.5 0.5];   % Starting point

最適点 x と最適点 fval における関数値を要求して、ソルバーを呼び出します。

[x,fval] = patternsearch(ObjectiveFunction,x0,[],[],[],[],lb,ub, ...
    ConstraintFunction)

Optimization finished: mesh size less than options.MeshTolerance 
and constraint violation is less than options.ConstraintTolerance.

x = 1×2

    0.8122   12.3122

fval = 
9.1324e+04

視覚化を追加する

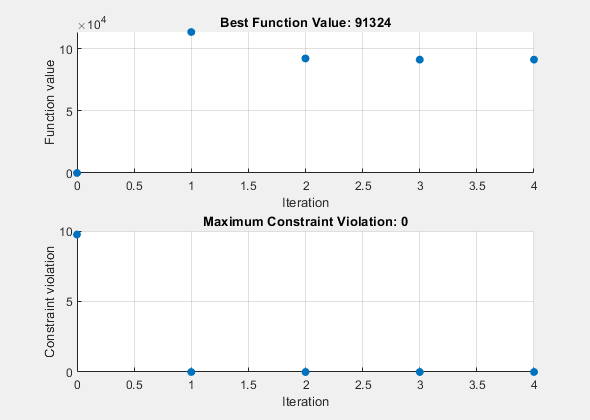
ソルバーの進行状況を観察するには、2 つのプロット関数を選択するオプションを指定します。プロット関数 psplotbestf は、各反復における最適な目的関数の値をプロットし、プロット関数 psplotmaxconstr は、各反復における最大制約違反をプロットします。これら 2 つのプロット関数をセル配列に設定します。また、Display オプションを 'iter' に設定して、コマンド ウィンドウにソルバーの進行状況に関する情報を表示します。

options = optimoptions(@patternsearch,'PlotFcn',{@psplotbestf,@psplotmaxconstr}, ...
                                      'Display','iter');

options 引数を含めてソルバーを実行します。

[x,fval] = patternsearch(ObjectiveFunction,x0,[],[],[],[],lb,ub, ...
    ConstraintFunction,options)

                                      Max
  Iter   Func-count       f(x)      Constraint   MeshSize      Method
    0         1     0.373958         9.75       0.9086    
    1        18       113581    1.617e-10        0.001   Increase penalty
    2       147        92267            0        1e-05   Increase penalty
    3       373      91333.2            0        1e-07   Increase penalty
    4       638        91324            0        1e-09   Increase penalty
Optimization finished: mesh size less than options.MeshTolerance 
and constraint violation is less than options.ConstraintTolerance.

x = 1×2

    0.8122   12.3122

fval = 
9.1324e+04

非線形制約により、patternsearch は各反復で多くのサブ問題を解決します。プロットと反復表示の両方に示されているように、解決プロセスには反復がほとんどありません。ただし、反復表示の Func-count 列には、反復ごとに多数の関数評価が表示されます。プロットと反復表示の両方から、初期点が実行不可能であり、目的関数が初期点で低いことがわかります。解決プロセス中、目的関数の値は最初は増加し、その後最終値まで減少します。

参考文献

1] Dixon, L. C. W., and G .P. Szego (eds.).Towards Global Optimisation 2.North-Holland:Elsevier Science Ltd., Amsterdam, 1978.

参考

トピック

• 制約の作成