このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

パターン探索オプションの効果

この例では、パターン探索のいくつかのオプションの効果を示します。オプションには、プロット、停止基準、およびソリューションを高速化するためのその他のアルゴリズム制御が含まれます。patternsearch アルゴリズムで使用可能なオプションの一覧については、パターン探索アルゴリズムのオプションテーブル を参照してください。

基本的なパターン探索アルゴリズムは驚くほど単純です。現在のポイントの周りのシフトの有限メッシュを設定し、メッシュ ポイントで目的関数を評価し (ポーリング と呼ばれます)、改善された目的関数値が見つかった場合はメッシュ間隔を広げ、改善が見つからない場合は間隔を狭めます。詳細は、パターン探索ポーリングの仕組みを参照してください。この例では、いくつかのメッシュ スケーリング オプション、メッシュ サイズの停止基準、およびポーリングに加えて代替探索方法の使用の効果を示します。

パターン探索の問題を設定する

最小化する問題は、線形等式制約と不等式制約に従う 6 つの変数の二次関数です。この例を実行すると、目的関数 lincontest7 が利用可能になります。

type lincontest7

function y = lincontest7(x)
%LINCONTEST7 objective function.
%   y = LINCONTEST7(X) evaluates y for the input X. Make sure that x is a column 
%   vector, whereas objective function gets a row vector.

%   Copyright 2003-2017 The MathWorks, Inc.
x = x(:);

%Define a quadratic problem in terms of H and f 
H = [36 17 19 12  8 15; 
     17 33 18 11  7 14; 
     19 18 43 13  8 16;
     12 11 13 18  6 11; 
      8  7  8  6  9  8; 
     15 14 16 11  8 29];

f = [ 20 15 21 18 29 24 ]';
 
y = 0.5*x'*H*x + f'*x;

関数ハンドル @lincontest7 を目的関数として指定します。

objectiveFcn = @lincontest7;

目的関数は長さ 6 の行ベクトルを受け入れます。最適化の初期点を指定します。

x0 = [2 1 0 9 1 0];

制約 Aineq*x <= Bineq と Aeq*x = Beq を表す線形制約マトリックスを作成します。詳細は、線形制約を参照してください。

Aineq = [-8 7 3 -4 9 0 ];
Bineq = [7];
Aeq = [7 1 8 3 3 3; 5 0 5 1 5 8; 2 6 7 1 1 8; 1 0 0 0 0 0];
Beq = [84 62 65 1];

patternsearch ソルバーを実行し、解に到達するまでに必要な反復回数と関数評価回数をメモします。

[X1,Fval,Exitflag,Output] = patternsearch(objectiveFcn,x0,Aineq,Bineq,Aeq,Beq);

patternsearch stopped because the mesh size was less than options.MeshTolerance.

fprintf('The number of iterations is: %d\n', Output.iterations);

The number of iterations is: 80

fprintf('The number of function evaluations is: %d\n', Output.funccount);

The number of function evaluations is: 737

fprintf('The best function value found is: %g\n', Fval);

The best function value found is: 2189.18

視覚化を追加する

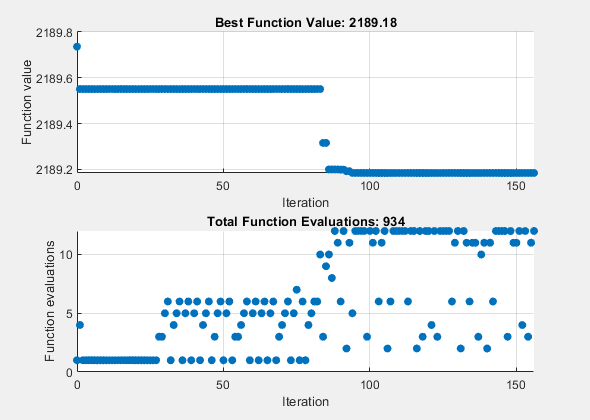
2 つのプロット関数を選択するオプションを指定して、最適化プロセスを監視します。プロット関数 psplotbestf は、反復ごとに最適な目的関数の値をプロットし、プロット関数 psplotfuncount は、反復ごとに目的関数が評価される回数をプロットします。これら 2 つのプロット関数をセル配列に設定します。

opts = optimoptions(@patternsearch,'PlotFcn',{@psplotbestf,@psplotfuncount});

opts 引数を含めて patternsearch ソルバーを実行します。この問題には上限制約や下限制約がなく、非線形制約もないため、7 番目、8 番目、9 番目の引数には空の配列 ([]) を渡します。

[X1,Fval,ExitFlag,Output] = patternsearch(objectiveFcn,x0,Aineq,Bineq, ...
    Aeq,Beq,[],[],[],opts);

patternsearch stopped because the mesh size was less than options.MeshTolerance.

メッシュオプション

パターン探索では、メッシュ内のポイントで目的関数を評価します。メッシュのサイズは解析速度に影響を与える可能性があります。オプションを使用してメッシュのサイズを制御できます。

初期メッシュサイズ

各反復におけるメッシュは、現在のメッシュ サイズによって拡大縮小され、現在のポイントに追加される一連の探索方向の範囲です。デフォルトでは、ソルバーは初期メッシュ サイズ 1 で開始されます。初期メッシュ サイズを 1/2 から開始するには、InitialMeshSize オプションを設定します。

opts = optimoptions(opts,'InitialMeshSize',1/2);

メッシュのスケーリング

メッシュをスケーリングして、スケーリングが不十分な最適化問題の最小化を改善できます。スケーリングでは、パターンをある程度回転させ、探索方向に沿ってスケーリングします。ScaleMesh オプションはデフォルトでオン (true) になっていますが、問題が適切にスケーリングされている場合はオフにすることができます。一般に、問題のスケールが不十分な場合は、このオプションを true に設定すると、関数評価の回数を減らすことができます。この問題では、lincontest7 が適切にスケールされた目的関数であるため、ScaleMesh を false に設定します。

opts = optimoptions(opts,'ScaleMesh',false);

メッシュアクセラレータ

直接探索法では、導関数ベースの最適化法に比べて多くの関数評価が必要になります。パターン探索アルゴリズムは、最適点の近傍を素早く見つけることができますが、最小値自体の検出には時間がかかる場合があります。patternsearch ソルバーは、アクセラレータを使用して関数評価の回数を削減できます。アクセラレータがオンの場合 (opts.AccelerateMesh = true)、ソルバーは最小メッシュ サイズに達した後、急速にメッシュ サイズを縮小します。このオプションは滑らかな問題にのみ推奨されます。他の種類の問題では、精度が多少低下する可能性があります。AccelerateMesh オプションはデフォルトではオフ (false) になっています。この問題では、目的関数が滑らかであるため、AccelerateMesh を true に設定します。

opts = optimoptions(opts,'AccelerateMesh',true);

patternsearch ソルバーを実行します。

[X2,Fval,ExitFlag,Output] = patternsearch(objectiveFcn,x0,Aineq,Bineq, ...
    Aeq,Beq,[],[],[],opts);

patternsearch stopped because the mesh size was less than options.MeshTolerance.

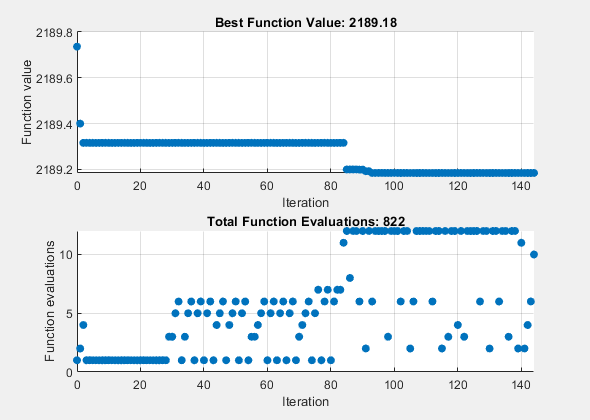
fprintf('The number of iterations is: %d\n', Output.iterations);

The number of iterations is: 146

fprintf('The number of function evaluations is: %d\n', Output.funccount);

The number of function evaluations is: 560

fprintf('The best function value found is: %g\n', Fval);

The best function value found is: 2189.18

メッシュ オプション設定により、反復回数と関数評価回数が削減されますが、精度の低下は見られません。

停止基準と許容範囲

MeshTolerance はメッシュ サイズの許容差です。メッシュ サイズが MeshTolerance より小さい場合、ソルバーは停止します。StepTolerance は、現在のポイントから次のポイントまでの変化に対する最小許容値です。FunctionTolerance は、現在のポイントから次のポイントまでの関数値の変化に対する最小許容値です。

MeshTolerance をデフォルト値の 10 分の 1 の 1e-7 に設定します。この設定により、関数評価と反復の回数が増え、より正確なソリューションが得られる可能性があります。

opts.MeshTolerance = 1e-7;

パターン探索における探索方法

パターン探索アルゴリズムは、SearchFcn オプションの値に基づいて、反復ごとに追加の探索方法を使用できます。SearchFcn を使用して探索方法を指定すると、patternsearch はメッシュ探索の前に指定された探索を最初に実行します。探索方法が成功した場合、patternsearch はその反復処理でメッシュ探索 (一般にポーリング関数と呼ばれる) をスキップします。探索方法で現在のポイントを改善できなかった場合、patternsearch はメッシュ探索を実行します。

SearchFcn には、最適化アルゴリズムである searchga や searchneldermead など、さまざまな探索方法を指定できます。これら 2 つの探索方法は、デフォルト設定である最初の反復でのみ使用します。これらのいずれかの方法をすべての反復で使用しても、結果が改善されず、計算コストが高くなる可能性があります。ただし、反復ごとに、または場合によっては 10 反復ごとに、ラテン超方格点を生成する searchlhs メソッドを使用できます。

探索方法の他の選択肢には、正基底 N+1 や正基底 2N などのポーリング方法があります。推奨される戦略は、探索方法として正基底 N+1 (パターンを作成するには最大で N+1 個のポイントが必要) を使用し、ポーリング方法として正基底 2N (パターンを作成するには 2N 個のポイントが必要) を使用することです。

探索方法として positivebasisnp1 を使用するようにオプション構造を更新します。PollFcn オプションでは正の基底 2N がデフォルトなので、このオプションを設定しないでください。

opts.SearchFcn = @positivebasisnp1;

patternsearch ソルバーを実行します。

[X5,Fval,ExitFlag,Output] = patternsearch(objectiveFcn,x0,Aineq,Bineq,Aeq,Beq, ...
    [],[],[],opts);

patternsearch stopped because the change in X and the mesh size were less than options.StepTolerance.

fprintf('The number of iterations is: %d\n', Output.iterations);

The number of iterations is: 44

fprintf('The number of function evaluations is: %d\n', Output.funccount);

The number of function evaluations is: 562

fprintf('The best function value found is: %g\n', Fval);

The best function value found is: 2189.18

メッシュ許容値が以前の値よりも小さくなり、ソルバーを停止する停止基準になったとしても、反復と関数評価の合計数は減少します。

参考

トピック

• メッシュオプションの設定
• パターン探索オプション
• カスタムプロット関数