このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。
パターン探索がワシントン山を登る
この例では、パターン探索によって関数を最適化する方法を視覚的に示します。この関数は、ワシントン山付近の地形の高さを x-y 位置の関数として表します。ワシントン山の頂上を見つけるには、高さの負の目的関数を最小化します。(この例のワシントン山は、米国北東部の最高峰です。)
米国地質調査所は、グリッド上の x-y 位置の関数として地形の高さに関するデータを提供しています。任意のポイントでの高さを評価できるように、目的関数は近くのグリッド ポイントから高さを補間します。
もちろん、max 関数を使用して、グリッドに指定された高さの最大値を単純に見つける方が速くなります。この例のポイントは、パターン探索アルゴリズムがどのように動作するかを示すことです。このアルゴリズムは、グリッド ポイントだけでなく、連続領域上で定義された関数に対しても機能します。また、目的関数を評価するのに計算コストが高い場合、max 関数で必要なように完全なグリッドでこの評価を実行すると、グリッド ポイントの小さなサブセットをサンプリングするパターン探索アルゴリズムを使用するよりもはるかに効率が悪くなります。
パターン探索の仕組み
パターン探索は、ポーリングと呼ばれる次の方法で目的関数の局所的最小値を見つけます。この説明では、パターン探索量を説明する単語は太字で表記されています。探索は初期点から開始され、最初のステップでは 現在のポイント として取得されます。
1.通常は座標方向のプラスとマイナスに メッシュ サイズ を掛けた点の パターン を生成し、このパターンを 現在の点 の中央に配置します。
2.パターン のすべてのポイントで目的関数を評価します。
3.パターン の最小目標が 現在のポイント の値よりも低い場合、ポーリングは 成功 となり、次の処理が行われます。
3a.見つかった最小のポイントが 現在のポイント になります。
3b.メッシュ サイズが 2 倍になります。
3c.アルゴリズムはステップ 1 に進みます。
4.ポーリングが 成功 しなかった場合、次の処理が行われます。
4a.メッシュ サイズが半分になります。
4b.メッシュ サイズがしきい値を下回ると、反復は停止します。
4c.それ以外の場合、現在のポイントが保持され、アルゴリズムはステップ 1 に進みます。
この単純なアルゴリズムは、いくつかの小さな変更を加えることで、最適化のための堅牢かつ簡単な方法を提供します。目的関数の勾配は必要ありません。制約にも適していますが、この例と説明では制約のない問題のみを扱います。
パターン探索の準備
パターン探索を準備するには、472 x 345 グリッドの USGS データを含む mtWashington.mat にデータをロードします。標高 Z はフィートで表されます。ベクトル x と y には、それぞれ東方向と北方向のグリッド間隔の基本値が含まれます。データ ファイルには、探索の開始点 X0 も含まれています。
load mtWashington目的関数の計算とプロット ルーチンを実行する 3 つの MATLAB ® ファイルがあります。内容は以下のとおりです。
1. terrainfun は、任意の x-y 位置での高さの負の値を評価します。terrainfun は、MATLAB 関数 interp2 を使用して 2 次元線形補間を実行します。Z データを取得し、すべての x-y ポイントでの高さの負の評価を可能にします。
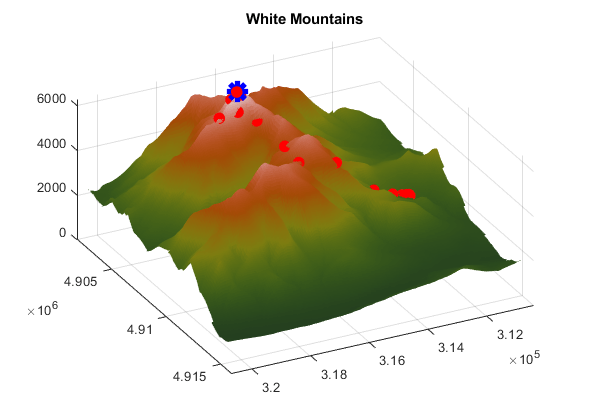
2. psoutputwashington は、ワシントン山の 3D レンダリングを描画します。さらに、実行が進むにつれて、各ポイントの周囲に、以前訪れたポイントよりも良い (高い) 球体が描画されます。
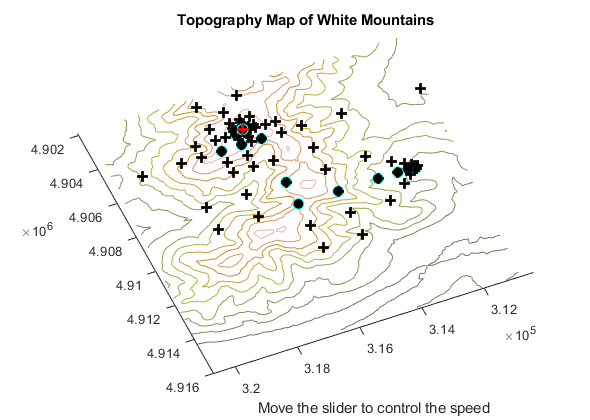
3. psplotwashington は、ワシントン山の等高線地図を描き、走行速度を制御するスライダーを監視します。パターン探索アルゴリズムが最適解を探す場所を、そのポイントに + 記号を描画することで示します。また、各ポイントの周囲に、以前訪れたポイントよりも優れた球体を描画します。
この例では、patternsearch は terrainfun を目的関数として使用し、psoutputwashington を出力関数として使用し、psplotwashington をプロット関数として使用します。匿名関数構文で patternsearch に渡す関数を準備します。
mtWashObjectiveFcn = @(xx) terrainfun(xx, x, y, Z); mtWashOutputFcn = @(xx,arg1,arg2) psoutputwashington(xx,arg1,arg2, x, y, Z); mtWashPlotFcn = @(xx,arg1) psplotwashington(xx,arg1, x, y, Z);
パターン探索オプションの設定
次に、パターン探索のオプションを作成します。このオプション セットでは、メッシュ サイズが 1 未満に縮小するとアルゴリズムが停止し、メッシュはスケールされず (各方向で同じサイズ)、初期メッシュ サイズは 10 に設定され、出力関数とプロット関数が設定されます。
options = optimoptions(@patternsearch,'MeshTolerance',1,'ScaleMesh',false, ... 'InitialMeshSize',10,'UseCompletePoll',true,'PlotFcn',mtWashPlotFcn, ... 'OutputFcn',mtWashOutputFcn,'UseVectorized',true);
パターン探索の進行を観察する
この例を実行すると、 2 つのウィンドウが表示されます。1 つは、パターン探索アルゴリズムがワシントン山の 2 次元等高線地図上で選択したポイントを示しています。このウィンドウには、アルゴリズムの反復間の遅延 (パターン探索の仕組みの説明のステップ 1 に戻るとき) を制御するスライダーがあります。スライダーを低い位置に設定すれば実行速度が速くなり、高い位置に設定すれば実行速度が遅くなります。
もう一方のウィンドウには、ワシントン山の 3 次元プロットと、パターン探索アルゴリズムが実行する手順が表示されます。実行中にこのプロットを回転させて、さまざまなビューを取得できます。
[xfinal ffinal] = patternsearch(mtWashObjectiveFcn,X0,[],[],[],[],[], ...
[],[],options)patternsearch stopped because the mesh size was less than options.MeshTolerance.
xfinal = 1×2
316130 4904295
ffinal = -6280
最後のポイント xfinal は、パターン探索アルゴリズムが終了した場所を示します。これは、ワシントン山の頂上の xy 位置です。最終的な目的関数 ffinal は、ワシントン山の高さ 6,280 フィートの負の値です。(ワシントン山天文台によれば、これは 6,288 フィートになるはずです)。
ファイル terrainfun.m、psoutputwashington.m、psplotwashington.m を調べて、補間とグラフィックスがどのように機能するかを確認します。
パターン探索アルゴリズムには多くのオプションがあります。たとえば、アルゴリズムは、パターン内のすべてのポイントをポーリングするのではなく、改善であるとわかった最初のポイントを取得できます。さまざまな順序でポイントをポーリングできます。また、ポーリングには決定論的パターンとランダムパターンの両方を使用できます。詳細については、Global Optimization Toolbox ユーザーズ ガイドを参照してください。