paretosearch

x = paretosearch(fun,nvars) は、多目的関数 fun の非劣点を見つけます。nvars 引数は最適化問題の次元 (決定変数の数) です。

x = paretosearch(fun,nvars,A,b) は、線形不等式 A*x ≤ b に従う非劣点を見つけます。線形不等式制約を参照してください。

x = paretosearch(fun,nvars,A,b,Aeq,beq) は、線形制約 Aeq*x = beq および A*x ≤ b に従って非劣点を見つけます。線形不等式が存在しない場合は、A = [] と b = [] を設定します。

x = paretosearch(fun,nvars,A,b,Aeq,beq,lb,ub) は x の設計変数の下限と上限のセットを定義し、x は常に lb ≤ x ≤ ub の範囲内になります。線形等式が存在しない場合は、Aeq = [] と beq = [] を設定します。x(i) に下限がない場合は、 lb(i) = -Inf を設定します。x(i) に上限がない場合は、 ub(i) = Inf を設定します。

x = paretosearch(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon) は、 nonlcon で定義された非線形不等式 c(x) を適用します。paretosearch 関数は、 c(x) ≤ 0 となる非優越点を見つけます。境界が存在しない場合は、lb = []、ub = []、またはその両方を設定します。

メモ

現在、paretosearch は非線形等式制約 ceq(x) = 0 をサポートしていません。

x = paretosearch(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options) は、 options で指定された最適化オプションを使用して非優越点を見つけます。optimoptions を使用してこれらのオプションを設定してください。非線形不等式制約または非線形等式制約がない場合は nonlcon = [] を設定します。

x = paretosearch(problem) は problem の非優越点を見つけます。ここで、 problem は problem で記述される構造です。

[x,fval] = paretosearch(___) は、任意の入力変数に対して、 x のすべてのソリューション (行) に対する fun のすべての目的関数の値である行列 fval を返します。出力 fval には nf 列があり、 nf は目的の数で、 x と同じ行数になります。

[x,fval,exitflag,output] = paretosearch(___) は、アルゴリズムが停止した理由を識別する整数である exitflag と、解決プロセスに関する情報を含む構造体である output も返します。

[x,fval,exitflag,output,residuals] = paretosearch(___) は、解点 x における制約値を含む構造体である residuals も返します。

例

パレート最前線を見つける

2 次元変数の 2 つの目的関数のパレート面上の点を見つけます。

fun = @(x)[norm(x-[1,2])^2;norm(x+[2,1])^2];
rng default % For reproducibility
x = paretosearch(fun,2);

Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

解を散布図としてプロットします。

plot(x(:,1),x(:,2),'m*')
xlabel('x(1)')
ylabel('x(2)')

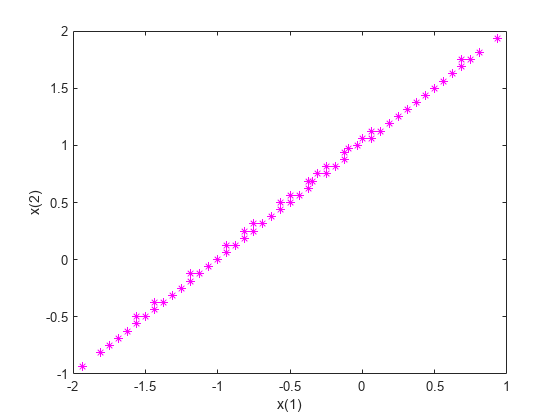
理論的には、この問題の解は [-2,-1] から [1,2] への直線です。paretosearch は、この直線に近い等間隔の点を返します。

線形制約によるパレートフロントの作成

線形制約 x(1) + x(2) <= 1 に従う 2 次元の 2 目的問題のパレートフロントを作成します。

fun = @(x)[norm(x-[1,2])^2;norm(x+[2,1])^2];
A = [1,1];
b = 1;
rng default % For reproducibility
x = paretosearch(fun,2,A,b);

Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

解を散布図としてプロットします。

plot(x(:,1),x(:,2),'m*')
xlabel('x(1)')
ylabel('x(2)')

理論的には、この問題の解は [-2,-1] から [0,1] への直線です。paretosearch は、この直線に近い等間隔の点を返します。

境界付きパレートフロントを作成する

境界 x(1) >= 0 と x(2) <= 1 に従う 2 次元の 2 目的問題のパレートフロントを作成します。

fun = @(x)[norm(x-[1,2])^2;norm(x+[2,1])^2];
lb = [0,-Inf]; % x(1) >= 0
ub = [Inf,1]; % x(2) <= 1
rng default % For reproducibility
x = paretosearch(fun,2,[],[],[],[],lb,ub);

Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

解を散布図としてプロットします。

plot(x(:,1),x(:,2),'m*')
xlabel('x(1)')
ylabel('x(2)')

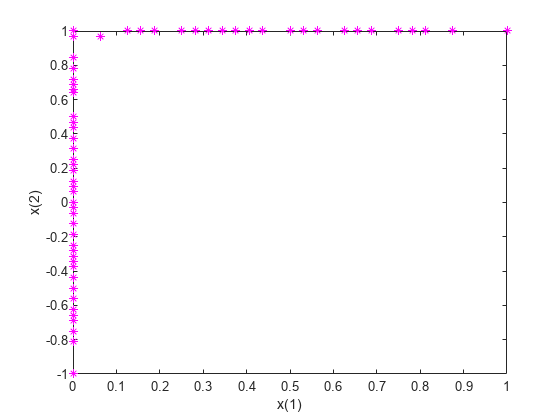
すべての解点は制約境界 x(1) = 0 または x(2) = 1 上にあります。

非線形制約を持つパレートフロントを作成する

境界 -1.1 <= x(i) <= 1.1 と非線形制約 norm(x)^2 <= 1.2 に従う 2 次元の 2 目的問題のパレートフロントを作成します。非線形制約関数はこの例の最後に表示され、この例をライブスクリプトとして実行すると機能します。それ以外の方法でこの例を実行するには、非線形制約関数を MATLAB® パス上のファイルとして含めます。

非線形制約の効果をよりよく確認するには、大きなパレートセットサイズを使用するようにオプションを設定します。

rng default % For reproducibility
fun = @(x)[norm(x-[1,2])^2;norm(x+[2,1])^2];
lb = [-1.1,-1.1];
ub = [1.1,1.1];
options = optimoptions('paretosearch','ParetoSetSize',200);
x = paretosearch(fun,2,[],[],[],[],lb,ub,@circlecons,options);

Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

解を散布図としてプロットします。円形制約境界のプロットを含めます。

figure
plot(x(:,1),x(:,2),'k*')
xlabel('x(1)')
ylabel('x(2)')
hold on
rectangle('Position',[-1.2 -1.2 2.4 2.4],'Curvature',1,'EdgeColor','r')
xlim([-1.2,0.5])
ylim([-0.5,1.2])
axis square
hold off

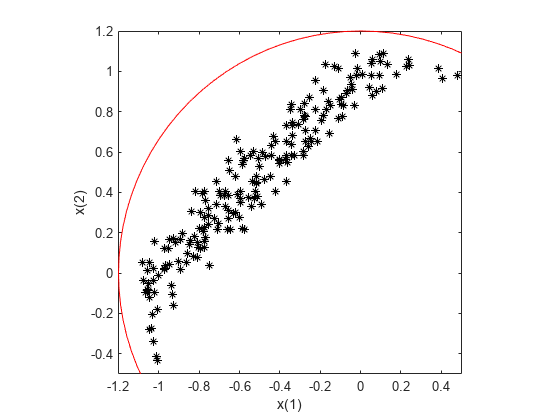
正の x(1) 値または負の x(2) 値を持つ解点は、非線形制約境界に近くなります。

function [c,ceq] = circlecons(x)
ceq = [];
c = norm(x)^2 - 1.2;
end

オプションを使用してパレートフロントを見つける

paretosearch の進行状況を監視するには、'psplotparetof' プロット関数を指定します。

fun = @(x)[norm(x-[1,2])^2;norm(x+[2,1])^2];
options = optimoptions('paretosearch','PlotFcn','psplotparetof');
lb = [-4,-4];
ub = -lb;
x = paretosearch(fun,2,[],[],[],[],lb,ub,[],options);

Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

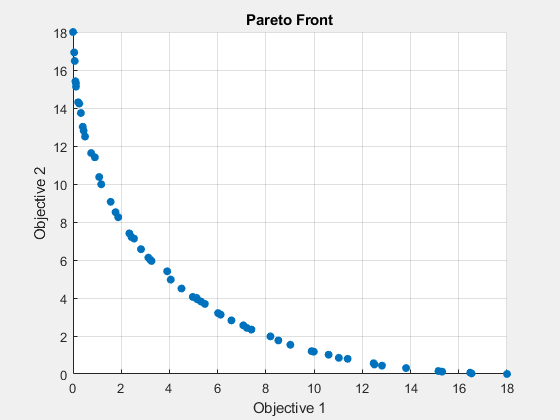
解は半径 18 の四分の一円弧のように見え、解析解であることが示されます。

関数空間とパラメータ空間でパレート最前線を見つける

x と fval の両方の出力を使用して paretosearch を呼び出すことにより、関数空間とパラメーター空間の両方でパレートフロントを取得します。関数空間とパラメーター空間の両方でパレート集合をプロットするためのオプションを設定します。

fun = @(x)[norm(x-[1,2])^2;norm(x+[2,1])^2];
lb = [-4,-4];
ub = -lb;
options = optimoptions('paretosearch','PlotFcn',{'psplotparetof' 'psplotparetox'});
rng default % For reproducibility
[x,fval] = paretosearch(fun,2,[],[],[],[],lb,ub,[],options);

Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

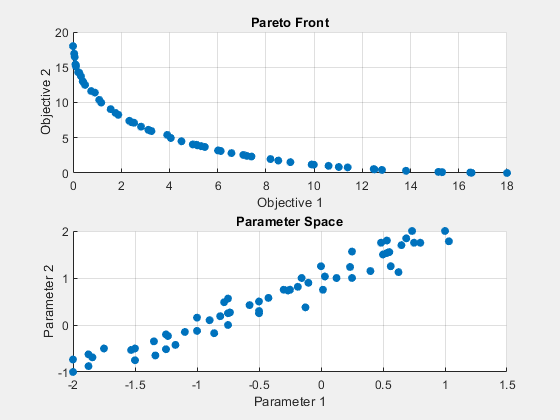
目的関数空間における解析解は、半径 18 の四分の一円弧です。パラメータ空間では、解析解は [-2,-1] から [1,2] への直線になります。解点は分析曲線に近くなります。

パレート集合ソリューションの監視

パレート集合の解決プロセスを監視するためのオプションを設定します。また、解決プロセスを理解できるように、paretosearch からさらに多くの出力を取得します。

options = optimoptions('paretosearch','Display','iter',...
    'PlotFcn',{'psplotparetof' 'psplotparetox'});
fun = @(x)[norm(x-[1,2])^2;norm(x+[2,1])^2];
lb = [-4,-4];
ub = -lb;
rng default % For reproducibility
[x,fval,exitflag,output] = paretosearch(fun,2,[],[],[],[],lb,ub,[],options);

Iter   F-count   NumSolutions  Spread       Volume 
   0        60        11          -         3.7872e+02
   1       386        12       7.6126e-01   3.4654e+02
   2       702        27       9.5232e-01   2.9452e+02
   3      1029        27       6.6332e-02   2.9904e+02
   4      1357        36       1.3874e-01   3.0070e+02
   5      1690        37       1.5379e-01   3.0200e+02
   6      2014        50       1.7828e-01   3.0252e+02
   7      2214        59       1.8536e-01   3.0320e+02
   8      2344        60       1.9435e-01   3.0361e+02
   9      2464        60       2.1055e-01   3.0388e+02

Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

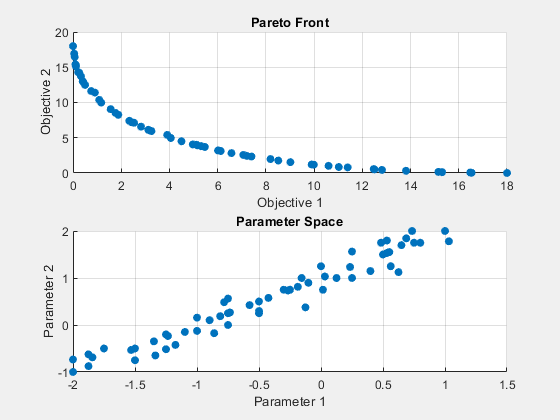
追加の出力を調べます。

fprintf('Exit flag %d.\n',exitflag)

Exit flag 1.

disp(output)

         iterations: 10
          funccount: 2464
             volume: 303.6076
    averagedistance: 0.0250
             spread: 0.2105
      maxconstraint: 0
            message: 'Pareto set found that satisfies the constraints. ...'
           rngstate: [1x1 struct]

パレート残差を取得する

パレートフロント制約残差を取得して調べます。線形不等式制約 sum(x) <= -1/2 と非線形不等式制約 norm(x)^2 <= 1.2 を持つ問題を作成します。精度を向上させるには、パレートフロントに 200 個のポイントを使用し、1e-7 の ParetoSetChangeTolerance を使用し、自然な境界 -1.2 <= x(i) <= 1.2 を指定します。

非線形制約関数はこの例の最後に表示され、この例をライブスクリプトとして実行すると機能します。それ以外の方法でこの例を実行するには、非線形制約関数を MATLAB® パス上のファイルとして含めます。

fun = @(x)[norm(x-[1,2])^2;norm(x+[2,1])^2];
A = [1,1];
b = -1/2;
lb = [-1.2,-1.2];
ub = -lb;
nonlcon = @circlecons;
rng default % For reproducibility
options = optimoptions('paretosearch','ParetoSetChangeTolerance',1e-7,...
    'PlotFcn',{'psplotparetof' 'psplotparetox'},'ParetoSetSize',200);

すべての出力を使用して paretosearch を呼び出します。

[x,fval,exitflag,output,residuals] = paretosearch(fun,2,A,b,[],[],lb,ub,nonlcon,options);

Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

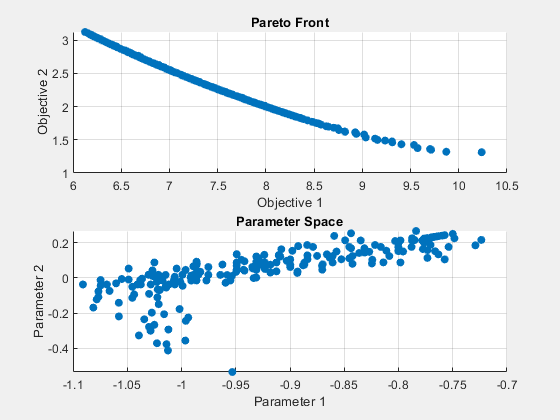
不等式制約により、制約のない集合と比較してパレート集合のサイズが縮小されます。返された残差を調べます。

fprintf('The maximum linear inequality constraint residual is %f.\n',max(residuals.ineqlin))

The maximum linear inequality constraint residual is 0.000000.

fprintf('The maximum nonlinear inequality constraint residual is %f.\n',max(residuals.ineqnonlin))

The maximum nonlinear inequality constraint residual is -0.000537.

返される残差の最大値は負であり、返されるポイントはすべて実行可能であることを意味します。返される残差の最大値はゼロに近いため、各制約がいくつかのポイントに対してアクティブであることを意味します。

function [c,ceq] = circlecons(x)
ceq = [];
c = norm(x)^2 - 1.2;
end

入力引数

`fun` — 最適化する目的関数
関数ハンドル | 関数名

最適化する目的関数。関数ハンドルまたは関数名として指定します。

fun は、長さ nvars の double x の実数行ベクトルを受け取り、目的関数値の実数ベクトル F(x) を返す関数です。fun の書き方の詳細については、目的関数を計算するを参照してください。

UseVectorized オプションを true に設定すると、fun はサイズが n 行 nvars 列の行列を受け入れます。ここで、行列は n 個の個体を表します。fun はサイズが n 行 m 列の行列を返します。ここで、m は目的関数の数です。適応度関数をベクトル化するを参照してください。

例: @(x)[sin(x),cos(x)]

データ型: char | function_handle | string

`nvars` — 変数の数
正の整数

変数の数。正の整数として指定されます。ソルバーは長さ nvars から fun の行ベクトルを渡します。

例: 4

データ型: double

`A` — 線形不等式制約
実数行列

線形不等式制約。実数行列として指定されます。A は M 行 nvars 列の行列で、M は不等式の数です。

A は M 個の線形不等式を符号化します。

A*x <= b,

ここで、x は nvars 個の変数 x(:) の列ベクトル、b は M 個の要素をもつ列ベクトルです。

例えば、

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

次の制約を与えます:

A = [1,2;3,4;5,6];
b = [10;20;30];

例: 制御変数の合計が 1 以下になるように指定するには、制約 A = ones(1,N) と b = 1 を指定します。

データ型: double

`b` — 線形不等式制約
実数ベクトル

実数ベクトルで指定される線形不等式制約です。b は、行列 A に関連する M 要素ベクトルです。b を行ベクトルとして渡す場合、ソルバーは b を列ベクトル b(:) に内部的に変換します。

b は M 個の線形不等式を符号化します。

A*x <= b,

ここで、x は N 個の変数 x(:) の列ベクトル、A は M 行 N 列の行列です。

例えば、

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

次の制約を与えます:

A = [1,2;3,4;5,6];
b = [10;20;30];

例: 制御変数の合計が 1 以下になるように指定するには、制約 A = ones(1,N) と b = 1 を指定します。

データ型: double

`Aeq` — 線形等式制約
実数行列

線形等式制約。実数行列として指定されます。Aeq は Me 行 nvars 列の行列で、Me は等式の数です。

Aeq は Me 個の線形等式を符号化します。

Aeq*x = beq,

ここで、x は N 個の変数 x(:) の列ベクトル、beq は Me 個の要素をもつ列ベクトルです。

例えば、

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

次の制約を与えます:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

例: 制御変数の合計が 1 になるように指定するには、制約 Aeq = ones(1,N) と beq = 1 を指定します。

データ型: double

`beq` — 線形等式制約
実数ベクトル

実数ベクトルで指定される線形等式制約です。beq は、行列 Aeq に関連する Me 要素ベクトルです。beq を行ベクトルとして渡す場合、ソルバーは beq を列ベクトル beq(:) に内部的に変換します。

beq は Me 個の線形等式を符号化します。

Aeq*x = beq,

ここで、x は N 個の変数 x(:) の列ベクトル、Aeq は Meq 行 N 列の行列です。

例えば、

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

次の制約を与えます:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

例: 制御変数の合計が 1 になるように指定するには、制約 Aeq = ones(1,N) と beq = 1 を指定します。

データ型: double

`lb` — 下限
`[]` (既定値) | 実数ベクトルまたは配列

下限。実数ベクトルまたは倍精度浮動小数点配列として指定します。lb は、 lb ≤ x ≤ ub 内の要素ごとの下限を表します。

paretosearch は配列 lb をベクトル lb(:) に内部的に変換します。

例: lb = [0;-Inf;4] は x(1) ≥ 0, x(3) ≥ 4 を意味します。

データ型: double

`ub` — 上限
`[]` (既定値) | 実数ベクトルまたは配列

上限は、実数ベクトルまたは倍精度浮動小数点数の配列として指定されます。ub は、 lb ≤ x ≤ ub 内の要素ごとの上限を表します。

paretosearch は配列 ub をベクトル ub(:) に内部的に変換します。

例: ub = [Inf;4;10] は x(2) ≤ 4, x(3) ≤ 10 を意味します。

データ型: double

`nonlcon` — 非線形制約
関数ハンドル | 関数名

非線形制約。関数ハンドルまたは関数名として指定されます。nonlcon は、行ベクトル x を受け取り、2 つの行ベクトル c(x) と ceq(x) を返す関数です。

c(x) は、 x における非線形不等式制約の行ベクトルです。paretosearch 関数は、 c のすべてのエントリに対して c(x) <= 0 を満たそうとします。
ceq(x) は [] を返す必要があります。現在、paretosearch は非線形等式制約をサポートしていないためです。

UseVectorized オプションを true に設定すると、nonlcon はサイズが n 行 nvars 列の行列を受け入れます。ここで、行列は n 個の個体を表します。nonlcon は、最初の引数にサイズが n 行 mc 列の行列を返します。ここで、mc は非線形不等式制約の数です。適応度関数をベクトル化するを参照してください。

たとえば、x = paretosearch(@myfun,nvars,A,b,Aeq,beq,lb,ub,@mycon) の場合、mycon は次の MATLAB^® 関数になります。

function [c,ceq] = mycon(x)
c = ...     % Compute nonlinear inequalities at x.
ceq = []    % No nonlinear equalities at x.

詳細については、非線形制約を参照してください。

データ型: char | function_handle | string

`options` — 最適化オプション
`optimoptions` の出力 | 構造体

最適化オプション。optimoptions の出力または構造体として指定されます。

{} はデフォルト値を示します。オプションの詳細については、パターン検索オプションを参照してください。

paretosearch のオプション

オプション	説明	値
`ConstraintTolerance`	制約に対する許容度。オプション構造の場合は、`TolCon` を使用します。	非負のスカラー \| `{1e-6}`
`Display`	表示レベル。	`'off'` \| `'iter'` \| `'diagnose'` \| `{'final'}`
`InitialPoints`	`paretosearch` の初期ポイント。次のいずれかのデータ型を使用します。 `nvars` 列の行列。各行は 1 つの初期点を表します。次のフィールドを含む構造体 (`X0` を除くすべてのフィールドはオプションです): `X0` — `nvars` 列を持つ行列。各行は 1 つの初期点を表します。 `Fvals` — `numObjectives` 列の行列。各行は `X0` 内の対応するポイントにおける目的関数の値を表します。 `Cineq` — `numIneq` 列の行列。各行は `X0` 内の対応する点における非線形不等式制約値を表します。 `paretosearch` は、`Fvals` フィールドと `Cineq` フィールドの欠損値を計算します。	`nvars` 列のマトリックス \| 構造 \| `{[]}`
`MaxFunctionEvaluations`	目的関数評価の最大数。オプション構造の場合は、`MaxFunEvals` を使用します。	非負の整数 \| `patternsearch` の場合は `{'2000numberOfVariables'}`、`paretosearch` の場合は `{'3000(numberOfVariables+numberOfObjectives)'}`。ここで、`numberOfVariables` は問題変数の数、`numberOfObjectives` は目的関数の数です。
`MaxIterations`	反復最大回数オプション構造の場合は、`MaxIter` を使用します。	非負の整数 \| `patternsearch` の場合は `{'100numberOfVariables'}`、`paretosearch` の場合は `{'100(numberOfVariables+numberOfObjectives)'}`。ここで、`numberOfVariables` は問題変数の数、`numberOfObjectives` は目的関数の数です。
`MaxTime`	最適化に許可される合計時間 (秒単位)。オプション構造の場合は、`TimeLimit` を使用します。	非負のスカラー \| `{Inf}`
`MeshTolerance`	メッシュサイズの許容範囲。オプション構造の場合は、`TolMesh` を使用します。	非負のスカラー \| `{1e-6}`
`MinPollFraction`	ポーリングするパターンの最小部分。	0 から 1 までのスカラー \| `{0}`
`OutputFcn`	最適化関数が各反復で呼び出す関数。関数ハンドルまたは関数ハンドルのセル配列として指定します。オプション構造の場合は、`OutputFcns` を使用します。	関数ハンドルまたは関数ハンドルのセル配列 \| `{[]}`
`ParetoSetChangeTolerance`	反復ウィンドウ内の停止測定値の相対的な変化が `ParetoSetChangeTolerance` 以下になると、ソルバーは停止します。目標が 3 つ以下の場合、`paretosearch` はボリュームとスプレッドの測定を使用します。 4 つ以上の目標の場合、`paretosearch` は広がりと距離の測定を使用します。 paretosearch アルゴリズムの定義を参照してください。適用可能な測定値の相対的な変化が `ParetoSetChangeTolerance` 未満になるか、これらの測定値の時系列の二乗フーリエ変換の最大値が比較的小さい場合、ソルバーは停止します。paretosearch アルゴリズムを参照してください。メモ `ParetoSetChangeTolerance` < `sqrt(eps)` ~ 1.5e-8 の設定は推奨されません。	非負のスカラー \| `{1e-4}`
`ParetoSetSize`	パレート集合内の点の数。	正の整数 \| `{'max(numberOfObjectives, 60)'}`、`numberOfObjectives`は目的関数の数
`PlotFcn`	パターン検索からの出力のプロット。組み込みプロット関数の名前、関数ハンドル、または組み込みプロット関数または関数ハンドルの名前のセル配列として指定します。オプション構造の場合は、`PlotFcns` を使用します。	`{[]}` \| `'psplotfuncount'` \| `'psplotmaxconstr'` \| カスタムプロット関数複数の目的がある場合: `'psplotdistance'` \| `'psplotparetof'` \| `'psplotparetox'` \| `'psplotspread'` \| `'psplotvolume'` 目標は一つ: `'psplotbestf'` \| `'psplotmeshsize'` \| `'psplotbestx'`
`PollMethod`	パターン検索で使用されるポーリング戦略。メモ問題に線形等式制約がある場合は、MADS ポーリングは使用できません。	`{'GPSPositiveBasis2np2'}` `\|` `'GPSPositiveBasis2N'` `\|` `'GPSPositiveBasisNp1'` `\|` `'GSSPositiveBasis2N'` `\|` `'GSSPositiveBasisNp1'` `\|` `'MADSPositiveBasis2N'` `\|` `'MADSPositiveBasisNp1'` `\|` `'GSSPositiveBasis2np2'`
`UseParallel`	目的関数と非線形制約関数を並列に計算します。ベクトル化と並列化のオプションおよびGlobal Optimization Toolbox で並列処理を使用する方法を参照してください。メモ `patternsearch` でベクトル化または並列ポーリングを使用するには、`UseCompletePoll` を `true` に設定する必要があります。同様に、ベクトル化または並列検索の場合は `UseCompleteSearch` を `true` に設定します。 R2019a 以降では、`UseParallel` オプションを `true` に設定すると、`patternsearch` が内部的に `UseCompletePoll` 設定を `true` にオーバーライドし、関数が並列にポーリングするようになります。	`true` \| `{false}`
`UseVectorized`	関数がベクトル化されるかどうかを指定します。ベクトル化と並列化のオプションおよび目的関数と制約関数をベクトル化するを参照してください。メモ `patternsearch` でベクトル化または並列ポーリングを使用するには、`UseCompletePoll` を `true` に設定する必要があります。同様に、ベクトル化または並列検索の場合は `UseCompleteSearch` を `true` に設定します。オプション構造の場合は、`Vectorized` = `'on'` または `'off'` を使用します。	`true` \| `{false}`

例: options = optimoptions('paretosearch','Display','none','UseParallel',true)

`problem` — 問題構造体
構造体

次のフィールドをもつ構造体として指定される問題構造体です。

objective — 目的関数
nvars — 変数の数
Aineq — 線形不等式制約の行列
bineq — 線形不等式制約のベクトル
Aeq — 線形等式制約の行列
beq — 線形等式制約のベクトル
lb — x の下限
ub — x の上限
nonlcon — 非線形制約関数
solver — 'paretosearch'
options — optimoptions で作成されたオプション
rngstate — 乱数ジェネレータの状態をリセットするためのオプションフィールド

メモ

problem のすべてのフィールドは必須ですが、rngstate はオプションです。

データ型: struct

出力引数

`x` — パレート点
`m` 行 `nvars` 列の配列

パレートポイントは、m 行 nvars 列の配列として返されます。ここで、m はパレートフロント上のポイントの数です。x の各行は、パレート面上の 1 つの点を表します。

`fval` — パレートフロント上の関数値
`m` 行 `nf` 列の配列

パレートフロント上の関数値は、m 行 nf 列の配列として返されます。m はパレートフロント上の点の数、nf は目的関数の数です。fval の各行は、 x の 1 つのパレート点における関数値を表します。

`exitflag` — `paretosearch` の停止理由
整数

paretosearch が停止した理由は、この表の整数値の 1 つとして返されます。

終了フラグ	停止条件
`1`	以下の条件のいずれかが満たされます。すべての暫定解のメッシュサイズが `options.MeshTolerance` より小さく、制約 (ある場合) が `options.ConstraintTolerance` 内で満たされている。パレートセットの広がりの相対変化が `options.ParetoSetChangeTolerance` より小さく、制約 (ある場合) が `options.ConstraintTolerance` 内で満たされている。パレートセットの容積の相対変化が `options.ParetoSetChangeTolerance` より小さく、制約 (ある場合) が `options.ConstraintTolerance` 内で満たされている。
`0`	反復回数が `options.MaxIterations` を超過、または関数評価の回数が `options.MaxFunctionEvaluations` を超過しています。
`-1`	最適化は出力関数またはプロット関数によって停止されます。
`-2`	すべての制約を満たす点をソルバーが見つけられません。
`-5`	最適化時間が `options.MaxTime` を超過しています。

`output` — 最適化プロセスに関する情報
構造体

最適化プロセスに関する情報。次のフィールドをもつ構造体として返されます。

iterations — 合計反復回数。
funccount — 関数評価の合計回数。
volume — 関数空間内のパレート点から形成された集合のハイパーボリューム。paretosearch アルゴリズムの定義を参照してください。
averagedistance — 関数空間におけるパレート点の平均距離測定。paretosearch アルゴリズムの定義を参照してください。
spread — パレート点の平均拡散度。paretosearch アルゴリズムの定義を参照してください。
maxconstraint — 最大制約違反（ある場合）。
message — アルゴリズムが終了した理由。
rngstate — アルゴリズムが開始する直前の MATLAB 乱数ジェネレーターの状態。'MADSPositiveBasis2N' などのランダムポーリングメソッドを使用する場合、または初期母集団を作成するデフォルトの準ランダムメソッドを使用する場合は、rngstate の値を使用して出力を再現できます。ga に対する同一の手法について説明している結果を再現するを参照してください。

`residuals` — `x` での制約残差
構造体

x での制約残差は、これらのフィールドを含む構造体として返されます (フィールドサイズの用語とエントリの用語集は表の後に続きます)。

フィールド名	フィールドサイズ	エントリ
`lower`	`m` 行 `nvars` 列	`lb` – `x`
`upper`	`m` 行 `nvars` 列	`x` – `ub`
`ineqlin`	`m` 行 `ncon` 列	`A*x - b`
`eqlin`	`m` 行 `ncon` 列	`\|Aeq*x - b\|`
`ineqnonlin`	`m` 行 `ncon` 列	`c(x)`

m — パレート面上の返されたポイントの数 x
nvars — 制御変数の数
ncon — 関連するタイプの制約の数（Aの行数や返された非線形等式の数など）
c(x) — 非線形制約関数の数値

詳細