多目的最適化とは

このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

複数の制約を伴う単一の目的では、直面している問題を適切に表せない可能性があるため、複数の目的で問題を定式化する必要がある場合があります。もしそうなら、何らかの方法でトレードオフしなければならない目標のベクトル、

F(x) = [F₁(x), F₂(x),...,F_m(x)],

(1)

が存在します。これらの目標の相対的な重要性は、システムの最高の機能が決定され、目標間のトレードオフが完全に理解されるまで、通常はわかりません。目標の数が増えると、トレードオフは複雑になり、定量化が難しくなる可能性があります。設計者は、最適化サイクル全体を通じて自分の直感と好みを表現する能力に頼る必要があります。したがって、多目的設計戦略の要件は、自然な問題の定式化を表現でき、問題を解決し、数値的に扱いやすく現実的な設計問題に好みを入力できることです。

多目的最適化は、多数の制約または境界の対象となる目的ベクトルF(x)の最小化に関係しています:

$\begin{array}{l} \min_{x \in ℝ^{n}} F (x), subject to \\ G_{i} (x) = 0, i = 1, ..., k_{e}; G_{i} (x) \leq 0, i = k_{e} + 1, ..., k; l \leq x \leq u . \end{array}$

F(x) はベクトルなので、F(x) のいずれかの要素が競合する場合、この問題には一意の解がないことに注意してください。代わりに、Zadeh [4] の非劣性の概念 (Censor [1] および Da Cunha と Polak [2] ではパレート最適性とも呼ばれる) を使用して目的を特徴付ける必要があります。非劣性ソリューションとは、1 つの目的を改善するには別の目的を低下させる必要があるソリューションです。この概念をより正確に定義するために、パラメーター空間内の実行可能領域 Ω を考えてみましょう。x は、すべての制約を満たす n 次元の実数 $x \in ℝ^{n}$ の要素です。つまり、

$Ω = {x \in ℝ^{n}},$

は

$\begin{array}{l} G_{i} (x) = 0, i = 1, ..., k_{e}, \\ G_{i} (x) \leq 0, i = k_{e} + 1, ..., k, \\ l \leq x \leq u . \end{array}$

に従います。これにより、目的関数空間 Λ の対応する実行可能領域を定義できます。

$Λ = {y \in ℝ^{m} : y = F (x), x \in Ω} .$

パフォーマンスベクトル F(x) は、図図 14-1、パラメーター空間から目的関数空間へのマッピングに 2 次元で表されているように、パラメーター空間を目的関数空間にマッピングします。

図 14-1、パラメーター空間から目的関数空間へのマッピング

非劣性解点を定義できるようになりました。

定義:点 $x * \in Ω$ は、x*の近傍において、 $(x * + Δ x) \in Ω$ と

$\begin{array}{l} F_{i} (x * + Δ x) \leq F_{i} (x *), i = 1, ..., m, and \\ F_{j} (x * + Δ x) < F_{j} (x *) for at least one j . \end{array}$

が成り立つようなΔxが存在しないとき、非劣解である。

図図 14-2、非劣性ソリューションの集合の2次元表現において、非劣解の集合はCとDの間の曲線上にあります。点AとBは、特定の非劣点を表します。

図 14-2、非劣性ソリューションの集合

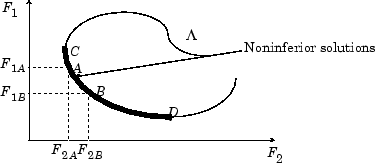
A と B は明らかに非劣勢の解決ポイントです。なぜなら、一方の目的 F₁ の改善には、もう一方の目的 F₂、つまり F_1B < F_1A, F_2B > F_2A の低下が必要であるからです。

Ω 内の劣った点は、すべての目的において改善が達成できる点を表すため、そのような点には価値がないことは明らかです。したがって、多目的最適化は、非劣性解点の世代と選択に関係します。

非劣性ソリューションは、パレート最適とも呼ばれます。多目的最適化における一般的な目標は、パレート最適解を構築することです。

多目的最適化とは

参考

トピック