gamultiobj アルゴリズム

このページは機械翻訳を使用して翻訳されました。元の英語を参照するには、ここをクリックします。

`gamultiobj` アルゴリズム

はじめに

このセクションでは、gamultiobj がパレート最適解上の点のセットを作成するために使用するアルゴリズムについて説明します。gamultiobj は、制御されたエリート遺伝的アルゴリズム (NSGA-II [3] のバリアント) を使用します。エリート主義的な GA は常に、適応度値 (ランク) がより高い個体を優先します。制御されたエリート GA は、適応度値が低い場合でも、集団の多様性を高めるのに役立つ個体を優先します。

多目的用語

gamultiobj アルゴリズムの用語のほとんどは遺伝的アルゴリズムの用語と同じです。ただし、このセクションで説明する追加の用語がいくつかあります。用語とアルゴリズムの詳細については、Deb [3] を参照してください。

優位性 — ベクトル値の目的関数 f に対して、点 x が点 y を優位にするのは次の場合です。
f_i(x) ≤ f_i(y) であり、すべての i が成立します。
f_j(x) < f_j(y) であり、一部の j が成立します。
「支配する」という用語は「劣る」という用語と同義です。y が x より劣っているときに、x は y を支配します。
点の集合 P 内の 非優越集合 は、 P のどの点によっても優越されない P 内の点 Q の集合です。
ランク — 実行可能な個体の場合、個体のランクの反復的な定義があります。ランク 1 の個体は他の個体によって支配されません。ランク 2 の個体はランク 1 の個体によってのみ支配されます。一般的に、ランク k の個体は、ランク k - 1 以下の個体によってのみ支配されます。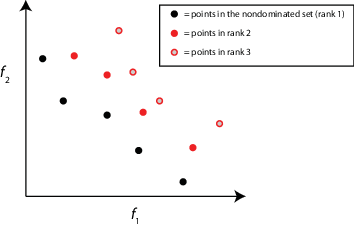
ランクが低いほど選ばれる可能性が高くなります（ランクが低いほど良い）。
実行不可能な個体はすべて、実行可能な個体よりもランクが低くなります。実行不可能な集団内では、順位はソートされた実行不可能性の尺度による順序に、実行可能なメンバーの最高順位を加えたものになります。
gamultiobj はランクを使用して親を選択します。
混雑距離 — 混雑距離は、個体とその最も近い隣人との近さの尺度です。gamultiobj アルゴリズムは、同じランクの個体間の距離を測定します。デフォルトでは、アルゴリズムは目的関数空間で距離を測定します。ただし、DistanceMeasureFcn オプションを {@distancecrowding,'genotype'} に設定することで、決定変数空間 (設計変数空間とも呼ばれます) で距離を測定することができます。
アルゴリズムは、極端な位置にある個体間の距離を Inf に設定します。残りの個体については、アルゴリズムは、個体のソートされた近隣個体間の正規化された絶対距離の次元の合計として距離を計算します。つまり、次元 m とソートされスケールされた個々の i の場合:
distance(i) = sum_m(x(m,i+1) - x(m,i-1)).
アルゴリズムは各次元を個別にソートするため、neighbors という用語は各次元の近隣を意味します。
同じランクでも距離が大きい個体は選択される可能性が高くなります (距離が大きいほど良い)。
デフォルトの @distancecrowding 関数とは異なる混雑距離測定を選択できます。多目的オプションを参照してください。
混雑距離は、停止基準の一部である拡散を計算する際の要素の 1 つです。混雑距離は、トーナメントの選択において、選ばれた 2 人の個人が同じ順位である場合に、同点判定の基準としても使用されます。
スプレッド — スプレッドはパレート集合の動きを表す尺度です。広がりを計算するために、gamultiobj アルゴリズムはまず、有限距離のパレートフロント上にあるポイントの混雑距離の標準偏差である σ を評価します。Q はこれらのポイントの数、d はこれらのポイント間の平均距離の測定値です。次に、アルゴリズムは、そのインデックスの現在の最小値のパレート点と、前の反復におけるそのインデックスの最小点との差のノルムの k 個の目的関数インデックスの合計である μ を評価します。スプレッドは
spread = (μ + σ)/(μ + Qd).
極端な目的関数の値が反復間であまり変化しない (つまり、μ が小さい) 場合、およびパレートフロント上の点が均等に分散している (つまり、σ が小さい) 場合、分散は小さくなります。
gamultiobj は停止条件でスプレッドを使用します。スプレッドがあまり変化せず、最終的なスプレッドが最近のスプレッドの平均よりも小さくなると、反復は停止します。停止条件を参照してください。

初期化

gamultiobj アルゴリズムの最初のステップは、初期集団を作成することです。アルゴリズムによって集団が作成されますが、InitialPopulationMatrix オプション (人口オプションを参照) を使用して初期集団または部分的な初期集団を指定することもできます。集団内の個体数は、PopulationSize オプションの値に設定されます。デフォルトでは、gamultiobj は境界と線形制約に関しては実行可能な集団を作成しますが、非線形制約に関しては必ずしも実行可能とは限りません。制約がない場合、または境界制約のみの場合はデフォルトの作成アルゴリズムは @gacreationuniform であり、線形または非線形制約がある場合は @gacreationlinearfeasible です。

gamultiobj は、母集団の目的関数と制約を評価し、それらの値を使用して母集団のスコアを作成します。

Iterations

gamultiobj アルゴリズムの主な反復は次のように進行します。

現在の集団の選択機能を使用して、次の世代の親を選択します。gamultiobj で使用できる唯一の組み込み選択関数はバイナリトーナメントです。カスタム選択機能を使用することもできます。
突然変異と交差によって、選択した親から子を作成します。
目的関数の値と実現可能性を計算して、子供たちにスコアを付けます。
現在の人口と子供を 1 つのマトリックス、つまり拡張人口に結合します。
拡張された集団内のすべての個体の順位と混雑距離を計算します。
各ランクの適切な数の個体を保持することで、拡張された集団を PopulationSize 個体になるようにトリミングします。

問題に整数または線形制約 (境界を含む) がある場合、アルゴリズムは集団の進化を変更します。整数と線形制約を参照してください。

停止条件

以下の停止条件が適用されます。各停止条件には終了フラグが関連付けられています。

終了フラグ値	停止条件
`1`	`options.MaxStallGenerations` 世代にわたるスプレッド値の相対的変化の幾何平均は `options.FunctionTolerance` 未満であり、最終的なスプレッドは過去 `options.MaxStallGenerations` 世代にわたる平均スプレッドよりも小さい
`0`	最大世代数を超えました
`-1`	出力関数またはプロット関数によって終了した最適化
`-2`	実行可能なポイントが見つかりません
`-5`	時間制限を超えました

終了フラグ 1 の場合、スプレッドの相対的変化の幾何平均は、k 世代前の相対的変化に対して ½^k の乗数を持ちます。

整数と線形制約

問題に整数または線形制約 (境界を含む) がある場合、アルゴリズムは集団の進化を変更します。

問題に整数制約と線形制約の両方がある場合、ソフトウェアは生成されたすべての個体をそれらの制約に関して実行可能になるように変更します。任意の作成、突然変異、または交差関数を使用でき、集団全体が整数制約と線形制約に関して実行可能なままになります。
問題に線形制約のみがある場合、ソフトウェアはそれらの制約に関して実行可能になるように個体を変更しません。線形制約に関して実現可能性を維持する作成、突然変異、および交差関数を使用する必要があります。そうしないと、人口が実現不可能になり、結果が実現不可能になる可能性があります。デフォルトの演算子は線形実行可能性を維持します: 作成の場合は gacreationlinearfeasible または gacreationnonlinearfeasible、突然変異の場合は mutationadaptfeasible、交差の場合は crossoverintermediate。

整数および線形実行可能性の内部アルゴリズムは、surrogateopt のアルゴリズムと似ています。問題に整数制約と線形制約がある場合、アルゴリズムはまず線形に実行可能な点を作成します。次に、アルゴリズムは、点を線形に実行可能な状態に保つヒューリスティックを使用して、線形に実行可能な点を整数に丸めることで、整数制約を満たそうとします。このプロセスで集団を構築するのに十分な実行可能なポイントを取得できなかった場合、アルゴリズムは intlinprog を呼び出して、境界、線形制約、および整数制約に関して実行可能なポイントをさらに見つけようとします。

その後、突然変異または交差によって新しい集団メンバーが作成されるときに、アルゴリズムは同様の手順を実行して、新しいメンバーが整数かつ線形実行可能であることを確認します。各新しいメンバーは、必要に応じて、整数および線形の制約と境界を満たしながら、元の値に可能な限り近くなるように変更されます。

参考文献

[1] Censor, Y. “Pareto Optimality in Multiobjective Problems,” Appl. Math. Optimiz., Vol. 4, pp 41–59, 1977.

[2] Da Cunha, N. O. and E. Polak. “Constrained Minimization Under Vector-Valued Criteria in Finite Dimensional Spaces,” J. Math. Anal. Appl., Vol. 19, pp 103–124, 1967.

[3] Deb, Kalyanmoy. “Multi-Objective Optimization using Evolutionary Algorithms,” John Wiley & Sons, Ltd, Chichester, England, 2001.

[4] Zadeh, L. A. “Optimality and Nonscalar-Valued Performance Criteria,” IEEE Trans. Automat. Contr., Vol. AC-8, p. 1, 1963.

参考

gamultiobj