このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

2つの目的のためのパレート フロント

R2025a

2つの目的を持つ多目的最適化

この例では、2 つの変数の 2 つの目的関数のパレート集合を見つける方法を示します。この例では、最小化のための 2 つの方法 (最適化ライブ エディター タスクの使用とコマンド ラインでの作業) を示します。

2目的関数f(x)（xも2次元）は、

f1(x)=x14+x24+x1x2−(x1x2)2−10x12f2(x)=x14+x24+x1x2−(x1x2)2.

最適化ライブ エディタータスクを使用してパレート集合を見つける

  1. [ホーム] タブの [ファイル] セクションで [新規ライブ スクリプト] ボタンをクリックして、新しいライブ スクリプトを作成します。

  2. 最適化ライブ エディター タスクを挿入します。[挿入] タブをクリックしてから、[コード] セクションで、[タスク]、[最適化] を選択します。

    Inserting Optimize Live Editor task

    Optimize task in Live Editor: Choose between problem-based (recommended) and solver-based

  3. Solver-based タスクをクリックします。

    Optimize Live Editor task

  4. 問題データの入力に使用するには、[Insert] タブの [セクション区切り] ボタンをクリックして新しいセクションを挿入します。新しいセクションがタスクの上と下に表示されます。

  5. タスクの上の新しいセクションで、次のコードを入力して、変数の数と下限と上限を定義します。 

    nvar = 2;
lb = [0 -5];
ub = [5 0];

  6. これらの変数をワークスペースに配置するには、Ctrl+Enter を押してセクションを実行します。

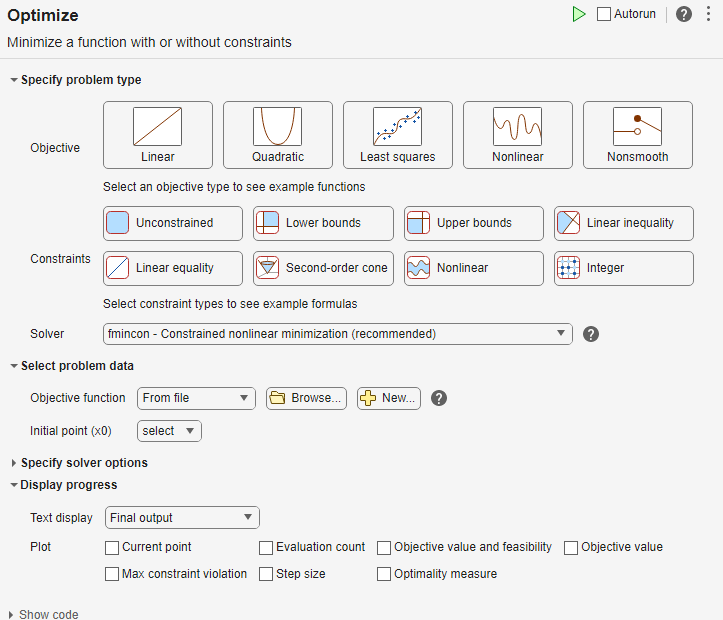
  7. 問題の種類の指定

    タスクの 問題の種類の指定 セクションで、目的 > 非線形 ボタンをクリックします。

  8. [制約] > [下限] ボタンと [上限] ボタンをクリックします。

  9. Solver > gamultiobj - Multiobjective optimization using genetic algorithmを選択します。

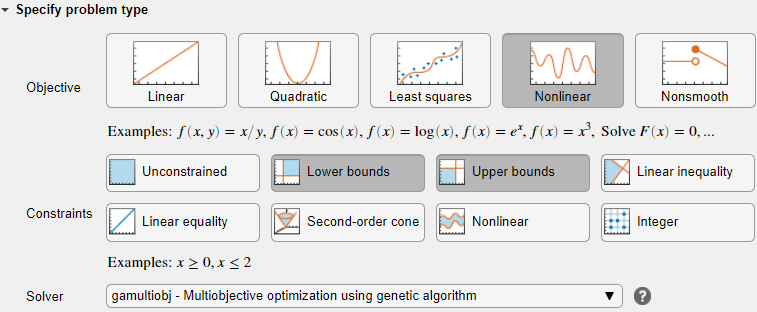
    Objective, constraints, and solver specified

  10. 問題データの選択

    問題のデータの選択 セクションで、[目的関数] > [ローカル関数] を選択し、新規 ボタンをクリックします。タスクの下側の新しいセクションに関数が表示されます。

  11. 結果の関数定義を編集して、次のコードを含めます。

    function f = mymulti1(x)

f(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - (x(1)*x(2))^2;
f(1) = f(2) - 10*x(1)^2;
end

  12. 問題のデータの選択 セクションで、ローカル関数 > mymulti1 関数を選択します。

  13. [変数の数] > [nvar] を選択します。

  14. [下限] > [ワークスペースから] > lbと[上限] > [ワークスペースから] > ubを選択します。

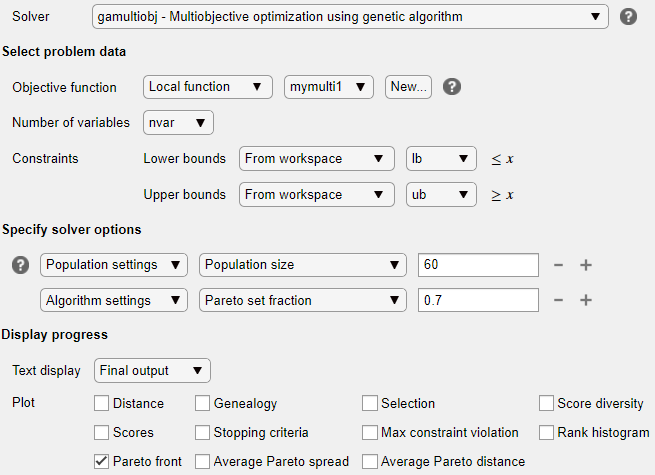
  15. ソルバーオプションを指定する

    タスクの ソルバー オプションの指定 セクションを展開し、 追加 ボタンをクリックします。より密度が高く、より連結されたパレート フロントを作成するには、Population settings > Population size > 60 を選択して、デフォルトよりも大きな母集団を指定します。

  16. デフォルト設定よりも多くの母集団をパレート フロントに配置するには、+ ボタンをクリックします。表示されたオプションから、Algorithm > Pareto set fraction > 0.7 を選択します。

  17. 表示オプションを設定する

    タスクの 進行状況の表示 セクションで、Pareto front プロット関数を選択します。

    Problem data, solver options, and display progress specified

  18. ソルバーの実行と結果の検証

    ソルバーを実行するには、タスク ウィンドウの右上にあるオプション ボタン [⁝] をクリックして、[セクションの実行] を選択します。別の Figure ウィンドウとタスク出力領域にプロットが表示されます。

    Set of points on a convex curve from about [-38,33] to about [-5,0]

    このプロットは、目的関数空間にプロットされた f の 2 つのコンポーネント間のトレードオフを示しています。詳細については、図 図 14-2、非劣性ソリューションの集合 を参照してください。

コマンドラインでパレート集合を見つける

同じ最適化をコマンド ラインで実行するには、次の手順を実行します。

  1. MATLAB® パスに mymulti1 目的関数ファイルを作成します。

    function f = mymulti1(x)

f(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - (x(1)*x(2))^2;
f(1) = f(2) - 10*x(1)^2;
end

  2. オプションと境界を設定します。

    options = optimoptions('gamultiobj','PopulationSize',60,...
          'ParetoFraction',0.7,'PlotFcn',@gaplotpareto);
lb = [0 -5];
ub = [5 0];

  3. オプションを使用して最適化を実行します。

    [solution,ObjectiveValue] = gamultiobj(@mymulti1,2,...
                          [],[],[],[],lb,ub,options);

最適化ライブ エディター タスクとコマンド ラインの両方を使用して問題を定式化して解決することができ、同じ結果が得られます。コマンドラインはより合理化されていますが、ソルバーの選択、問題の設定、プロット関数などのオプションの選択に関するヘルプは少なくなります。また、Optimize を使用して問題を開始し、[最適化] ライブ エディター タスクまたはソルバーを使用した制約付き非線形問題 のように、コマンド ラインで使用するためのコードを生成することもできます。

別の見方

この問題は他の観点から見ることもできます。次の図には、2 つの目的関数の水準曲線、gamultiobj によって計算されたパレート フロンティア (ボックス)、および真のパレート フロンティアの x 値 (ほぼ直線で接続されたひし形) のプロットが含まれています。真のパレート境界点は、目的関数のレベル曲線が平行になる点です。アルゴリズムは、目的関数の勾配が平行になる場所を見つけることによってこれらのポイントを計算します。この図はパラメーター空間にプロットされています。図 14-1、パラメーター空間から目的関数空間へのマッピング を参照してください。

目的関数の等高線とパレートフロンティア

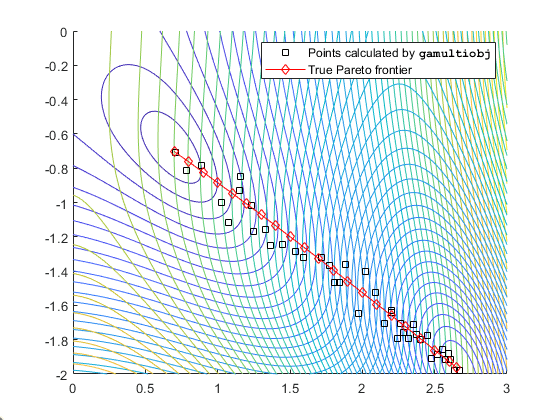
gamultiobj は線分の端点を見つけます。つまり、パレート限界の全範囲を見つけます。

最適化ライブ エディター タスクまたはコマンド ラインで最適化を実行して、ソリューション データ solution を作成します。

パレート最適曲線は、2 つの目的関数の勾配が正確に反対方向を指す、2 つの目的間の最適なトレードオフ曲線です。勾配は次のコードで gg と gf で指定されます。

function mout = mymulti2(x)
%
gg = [4*x(1)^3+x(2)-2*x(1)*(x(2)^2);
    x(1)+4*x(2)^3-2*(x(1)^2)*x(2)];
gf = gg - [20*x(1);0];

mout = gf(1)*gg(2) - gf(2)*gg(1);
2 つの勾配が平行の場合、mout = 0 になります。

このコードはプロットを作成します。

[x,y] = meshgrid(0:.01:3,-2:.01:0);
[myf,myg] = mymulti(x,y);
mygg = sqrt(myg+.26); % This spaces the contours better
myff = sqrt(myf+40); % This spaces the contours better
a = [.7,fzero(@(t)mymulti2([.7,t]),[-2;0])];
% fzero calculates where mout = 0
for jj = 0.8:0.1:2.6
    a = [a;[jj,fzero(@(t)mymulti2([jj,t]),[-2;0])]];
end
a = [a;[2.65,fzero(@(t)mymulti2([2.65,t]),[-2;0])]];
figure
hold on
contour(x,y,mygg,50)
contour(x,y,myff,50)
gam = plot(solution(:,1),solution(:,2),'ks');
tru = plot(a(:,1),a(:,2),'-dr');
legend([gam tru],'Points calculated by \bf{\fontname{Courier}gamultiobj}',...
    'True Pareto frontier')
hold off
関数 mymulti(x,y) は、多目的適応度関数のベクトル化されたバージョンです。
function [f,g] = mymulti(x,y)
%
g = x.^4 + y.^4 + x.*y - (x.^2).*(y.^2);
f = g - 10*x.^2;
end

参考

|

トピック