このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。
paretosearch アルゴリズム
paretosearchアルゴリズムの概要
paretosearch アルゴリズムは、一連のポイントに対してパターン探索を使用して、非優越ポイントを繰り返し探索します。多目的用語を参照してください。パターン探索は、各反復ですべての境界と線形制約を満たします。
理論的には、アルゴリズムは真のパレート フロントに近い点に収束します。収束についての議論と証明については、Custòdio et al. [1] を参照してください。その証明は、Lipschitz 連続目的関数と制約条件を持つ問題に適用されます。
paretosearchアルゴリズムの定義
paretosearch は、アルゴリズム内でいくつかの中間量と許容値を使用します。
| 数量 | 定義 |
|---|---|
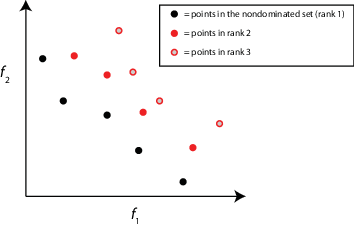
| ランク | ポイントのランクには反復的な定義があります。
|
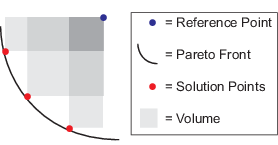
| ボリューム | 目的関数空間における点の集合pの超体積は、すべてのインデックスjに対して不等式を満たす。 fi(j) < pi < Mi, ここで、fi(j) はパレート集合内の j 番目の目的関数値の i 番目の要素であり、Mi はパレート集合内のすべてのポイントの i 番目の要素の上限です。この図では、M は参照点と呼ばれます。図の灰色の陰影は、一部の計算アルゴリズムが包含・除外計算の一部として使用する体積の部分を示しています。
詳細については、Fleischer [3] を参照してください。
ボリュームの変化はアルゴリズムを停止する要因の 1 つです。詳細は、停止条件を参照してください。 |
| 距離 | 距離は、個体とその最も近い隣人との近さを測る尺度です。 アルゴリズムは、極端な位置にある個体の距離を
アルゴリズムは各次元を個別に並べ替えるため、neighbors という用語は各次元の隣接要素を意味します。 同じランクであっても距離が大きい個体は選択される可能性が高くなります(距離が大きいほど良い)。 距離は、停止基準の一部である広がりの計算における要素の 1 つです。詳細は、停止条件を参照してください。 |
| 広がり | 広がりはパレート集合の動きを表す尺度です。広がりを計算するために、
極端な目的関数の値が反復間であまり変化しない (つまり、μ が小さい) 場合、およびパレート フロント上のポイントが均等に分散している (つまり、σ が小さい) 場合、分散は小さくなります。
|
ParetoSetChangeTolerance | 探索の停止条件。反復ウィンドウ内でボリューム、広がり、または距離が ParetoSetChangeTolerance 以上変化しない場合、paretosearch は停止します。詳細は、停止条件を参照してください。 |
MinPollFraction | 反復中にポーリングする場所の最小割合。 このオプションは、 |
paretosearchアルゴリズムのスケッチ
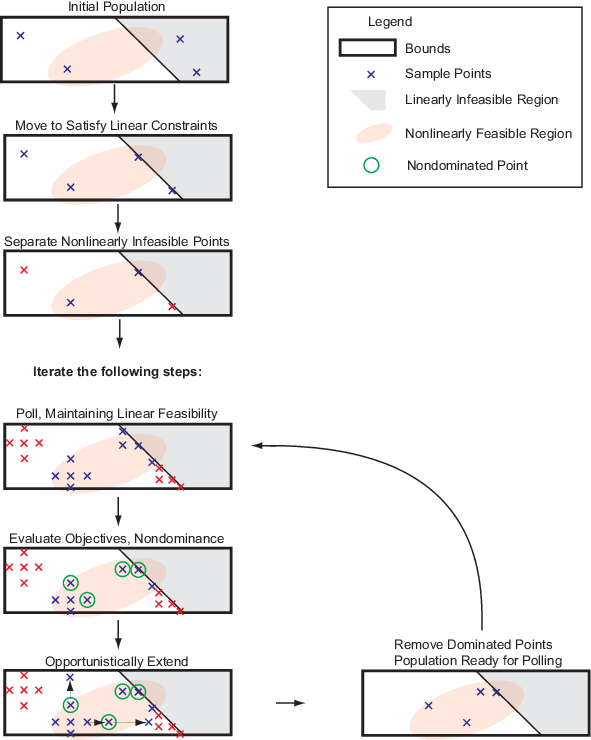
探索を初期化する
初期のポイント セットを作成するために、paretosearch はデフォルトで、問題の範囲に基づいて準ランダム サンプルから options.ParetoSetSize ポイントを生成します。詳細については、Bratley と Fox [2] を参照してください。問題の次元が 500 を超える場合、paretosearch は ラテンハイパーキューブ サンプリング を使用して初期点を生成します。
コンポーネントに境界がない場合、paretosearch は人工的な下限値 -10 と上限値 10 を使用します。
コンポーネントに境界が 1 つしかない場合、paretosearch はその境界を幅 20 + 2*abs(bound) の間隔の終点として使用します。たとえば、コンポーネントに上限がなく、下限が 15 の場合、paretosearch は 20 + 2*15 = 55 の間隔幅を使用するため、15 + 55 = 70 という人工的な上限を使用します。
options.InitialPoints でいくつかの初期点を渡すと、paretosearch はそれらのポイントを初期点として使用します。paretosearch は、必要に応じてさらにポイントを生成し、少なくとも options.ParetoSetSize の初期点を取得します。
次に、paretosearch は初期点をチェックし、境界と線形制約に関して実行可能であることを確認します。必要に応じて、paretosearch は線形計画問題を解くことによって、初期点を線形実行可能点の線形部分空間に投影します。このプロセスにより、いくつかのポイントが一致することがあり、その場合、paretosearch は重複するポイントを削除します。paretosearch は、人工的な境界の初期点を変更せず、指定された境界と線形制約に対してのみ変更します。
線形制約を満たすように点を移動した後、必要に応じて、paretosearch は点が非線形制約を満たしているかどうかを確認します。paretosearch は、すべての非線形制約を満たしていない点に Inf のペナルティ値を与えます。次に、paretosearch は残りの実行可能ポイントの欠落している目的関数値を計算します。
メモ
現在、paretosearch は非線形等式制約 ceq(x) = 0 をサポートしていません。
アーカイブと現職者の作成
paretosearch は 2 つのポイント セットを維持します。
archive—options.MeshTolerance未満のメッシュ サイズに関連付けられ、options.ConstraintTolerance内のすべての制約を満たす非優越点を含む構造。archive構造には2*options.ParetoSetSizeポイントしか含まれず、最初は空です。archive内の各ポイントには、ポイントが生成されたメッシュ サイズである関連付けられたメッシュ サイズが含まれています。iterates— 非支配点と、おそらく大きなメッシュ サイズまたは実行不可能性と関連付けられたいくつかの支配点を含む構造。iteratesの各ポイントには、関連付けられたメッシュ サイズが含まれます。iteratesには、最大options.ParetoSetSize個のポイントが含まれます。
より良いポイントを見つけるためのポーリング
paretosearch は iterates からポイントをポーリングし、ポーリングされたポイントは iterates のポイントから関連するメッシュ サイズを継承します。paretosearch アルゴリズムは、境界とすべての線形制約に関して実現可能性を維持するポーリングを使用します。
問題に非線形制約がある場合、paretosearch は各ポール点の実現可能性を計算します。paretosearch は、実行不可能なポイントのスコアを実行可能なポイントのスコアとは別に保持します。実行可能点のスコアは、その点の目的関数値のベクトルです。実行不可能な点のスコアは、非線形実行不可能性の合計です。
paretosearch は、iterates 内の各ポイントについて、少なくとも MinPollFraction*(パターン内のポイントの数) の位置をポーリングします。ポーリングされたポイントが、現職(元の)ポイントに対して少なくとも 1 つの非優位ポイントを与える場合、ポーリングは成功とみなされます。それ以外の場合、paretosearch は、非優勢ポイントが見つかるか、パターン内のポイントがなくなるまでポーリングを続けます。paretosearch がポイントを使い果たし、非優越ポイントを生成しない場合、paretosearch はポーリングが失敗したと宣言し、メッシュ サイズを半分にします。
ポーリングによって非優勢ポイントが見つかった場合、paretosearch は成功した方向にポーリングを繰り返し拡張し、拡張によって優勢ポイントが生成されるまで、メッシュ サイズをそのたびに 2 倍にします。この拡張中にメッシュ サイズが options.MaxMeshSize (デフォルト値: Inf) を超えると、ポーリングは停止します。目的関数の値が -Inf まで減少すると、paretosearch は問題が非有界であると宣言して停止します。
archive と iterates 構造を更新
iterates 内のすべてのポイントをポーリングした後、アルゴリズムは新しいポイントを iterates および archive 構造内のポイントと一緒に調べます。paretosearch は各ポイントのランク、つまりパレート フロント数を計算し、次の処理を実行します。
archiveでランク 1 ではないすべてのポイントを削除対象としてマークします。新しいランク
1ポイントをiteratesに挿入するためにマークします。iterates内で、関連付けられたメッシュ サイズがoptions.MeshToleranceより小さい実行可能なポイントをマークし、archiveに転送します。iterates内の支配点が、iteratesに新しい非支配点が追加されるのを妨げる場合にのみ、削除対象としてマークします。
次に、paretosearch は各ポイントの体積と距離の測定値を計算します。マークされたポイントが含まれることで archive がオーバーフローする場合は、最も大きなボリュームを持つポイントが archive を占有し、その他のポイントは残ります。同様に、iterates に追加するようにマークされた新しいポイントは、体積の順に iterates に入ります。
iterates がいっぱいで支配点がない場合、paretosearch は iterates に点を追加せず、反復が失敗したと宣言します。paretosearch は iterates のメッシュ サイズを 1/2 倍にします。
停止条件
目的関数が 3 つ以下の場合、paretosearch は停止手段としてボリュームと広がりを使用します。4 つ以上の目標の場合、paretosearch は距離と広がりを停止手段として使用します。この説明の残りの部分では、paretosearch が使用する 2 つの尺度を 適用可能な 尺度と呼びます。
アルゴリズムは、適用可能な測定値の最後の 8 つの値のベクトルを維持します。8 回の反復の後、アルゴリズムは各反復の開始時に 2 つの適用可能な測定値の値をチェックします (tol = options.ParetoSetChangeTolerance の場合)。
spreadConverged = abs(spread(end - 1) - spread(end)) <= tol*max(1,spread(end - 1));volumeConverged = abs(volume(end - 1) - volume(end)) <= tol*max(1,volume(end - 1));distanceConverged = abs(distance(end - 1) - distance(end)) <= tol*max(1,distance(end - 1));
いずれかの適用可能なテストが true の場合、アルゴリズムは停止します。それ以外の場合、アルゴリズムは、適用可能な測定値のフーリエ変換の二乗項の最大値から最初の項を引いた値を計算します。次に、アルゴリズムは最大値を削除された項 (変換の DC 成分) と比較します。削除されたいずれかの用語が 100*tol*(max of all other terms) より大きい場合、アルゴリズムは停止します。このテストでは、基本的に、測定値のシーケンスは変動しておらず、収束していることが判定されます。
さらに、プロット関数または出力関数によってアルゴリズムが停止したり、時間制限または関数評価制限を超えたためにアルゴリズムが停止したりする場合があります。
戻り値
アルゴリズムは、次のようにパレート フロント上の点を返します。
paretosearchは、archiveとiteratesのポイントを 1 つのセットに結合します。目的関数が 3 つ以下の場合、
paretosearchは、最大ボリュームから最小ボリュームまでのポイントを、最大ParetoSetSizeポイントまで返します。目的関数が 4 つ以上ある場合、
paretosearchは最大距離から最小距離までのポイントを最大ParetoSetSizeポイントまで返します。
並列計算とベクトル化関数評価のための変更
paretosearch が目的関数の値を並列またはベクトル化された形式で計算する場合 (UseParallel は true または UseVectorized は true です)、アルゴリズムにいくつかの変更が加えられます。
UseVectorizedがtrueの場合、paretosearchはMinPollFractionオプションを無視し、パターン内のすべてのポール点を評価します。並列計算を行う場合、
paretosearchはiterates内の各ポイントを順番に調べ、各ポイントから並列ポールを実行します。MinPollFractionの割合のポール点を返した後、paretosearchは、いずれかのポーリング ポイントがベース ポイントを支配しているかどうかを判断します。そうであれば、ポーリングは成功したとみなされ、他の並行評価は停止します。そうでない場合は、支配的なポイントが表示されるかポーリングが終了するまでポーリングは続行されます。paretosearchは、ワーカー上またはベクトル化された形式のいずれかで目的関数評価を実行しますが、両方では実行しません。UseParallelとUseVectorizedの両方をtrueに設定すると、paretosearchはワーカー上で目的関数の値を並列に計算しますが、ベクトル化されることはありません。この場合、paretosearchはMinPollFractionオプションを無視し、パターン内のすべてのポール点を評価します。
paretosearchを素早く実行する
paretosearch を実行する最も速い方法は、いくつかの要因によって異なります。
目的関数評価が遅い場合は、通常、並列コンピューティングを使用するのが最も速くなります。目的関数評価が高速な場合、並列コンピューティングのオーバーヘッドは大きくなる可能性がありますが、評価が低速な場合は、通常、より多くのコンピューティング能力を使用するのが最適です。
メモ
並列コンピューティングには Parallel Computing Toolbox™ ライセンスが必要です。
目的関数評価にそれほど時間がかからない場合は、通常、ベクトル化された評価を使用するのが最も高速です。ただし、ベクトル化された計算ではパターン全体が評価されるのに対し、シリアル評価ではパターンのごく一部のみが評価されるため、常にそうであるとは限りません。特に高次元では、評価回数の削減により、一部の問題では逐次評価が高速化される可能性があります。
ベクトル化コンピューティングを使用するには、目的関数が任意の行数の行列を受け入れる必要があります。各行は評価する 1 つのポイントを表します。目的関数は、受け入れる行数と同じ行数(目的関数ごとに 1 列)の目的関数値の行列を返す必要があります。単一目的の説明については、適応度関数をベクトル化する (
ga) または ベクトル化された目的関数 (patternsearch) を参照してください。
参照
[1] Custòdio, A. L., J. F. A. Madeira, A. I. F. Vaz, and L. N. Vicente. Direct Multisearch for Multiobjective Optimization. SIAM J. Optim., 21(3), 2011, pp. 1109–1140. Preprint available at https://www.researchgate.net/publication/220133323_Direct_Multisearch_for_Multiobjective_Optimization.
[2] Bratley, P., and B. L. Fox. Algorithm 659: Implementing Sobol’s quasirandom sequence generator. ACM Trans. Math. Software 14, 1988, pp. 88–100.
[3] Fleischer, M. The Measure of Pareto Optima: Applications to Multi-Objective Metaheuristics. In "Proceedings of the Second International Conference on Evolutionary Multi-Criterion Optimization—EMO" April 2003 in Faro, Portugal. Published by Springer-Verlag in the Lecture Notes in Computer Science series, Vol. 2632, pp. 519–533. Preprint available at https://api.drum.lib.umd.edu/server/api/core/bitstreams/4241d9c0-f514-4a41-bd58-07ac2538d918/content.