このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

全体的または複数の局所的最小値を見つける

この例では、GlobalSearch が大域的最小値を効率的に見つける方法と、MultiStart がより多くのローカル最小値を見つける方法を示しています。

この例の目的関数には、多くの局所最小値と一意の大域的最小値が存在します。極座標では、関数は

$$f(r,t)=g(r)h(t)$$

ここで、

$$\begin{array}{l}g(r)=\left(\sin (r)-\frac{\sin (2r)}{2}+\frac{\sin (3r)}{3}-\frac{\sin (4r)}{4}+4\right)\frac{r^2}{r+1}\\ h(t)=2+\cos (t)+\frac{\cos \left(2t-\frac{1}{2}\right)}{2}.\end{array}$$

関数 $$g$$ と $$h$$ をプロットし、関数 $$f$$ の表面プロットを作成します。

figure
subplot(1,2,1);
fplot(@(r)(sin(r) - sin(2*r)/2 + sin(3*r)/3 - sin(4*r)/4 + 4) .* r.^2./(r+1), [0 20])
title(''); ylabel('g'); xlabel('r');
subplot(1,2,2);
fplot(@(t)2 + cos(t) + cos(2*t-1/2)/2, [0 2*pi])
title(''); ylabel('h'); xlabel('t');

figure
fsurf(@(x,y) sawtoothxy(x,y), [-20 20])
% sawtoothxy is defined in the first step below
xlabel('x'); ylabel('y'); title('sawtoothxy(x,y)');
view(-18,52)

大域的最小値は $$r=0$$ で、目的関数は 0 です。関数 $$g(r)$$ は、$$r$$ 内でほぼ線形に増加し、鋸歯形状を繰り返します。関数 $$h(t)$$ には 2 つの局所最小値があり、そのうちの 1 つはグローバルです。

sawtoothxy.m ファイルは、直交座標から極座標に変換し、極座標で値を計算します。

type sawtoothxy

function f = sawtoothxy(x,y)
[t r] = cart2pol(x,y); % change to polar coordinates
h = cos(2*t - 1/2)/2 + cos(t) + 2;
g = (sin(r) - sin(2*r)/2 + sin(3*r)/3 - sin(4*r)/4 + 4) ...
    .*r.^2./(r+1);
f = g.*h;
end

GlobalSearch による単一の大域的最小値

GlobalSearch を使用して大域的最小値を探索するには、まず問題構造を作成します。fminconには'sqp'アルゴリズムを使用します。

problem = createOptimProblem('fmincon',...
    'objective',@(x)sawtoothxy(x(1),x(2)),...
    'x0',[100,-50],'options',...
    optimoptions(@fmincon,'Algorithm','sqp','Display','off'));

開始点は [0,0] ではなく [100,-50] なので、GlobalSearch は大域解から開始されません。

fmincon を実行して問題の構造を検証します。

[x,fval] = fmincon(problem)

x = 1×2

   45.7236 -107.6515

fval = 
555.5820

GlobalSearch オブジェクトを作成し、反復表示を設定します。

gs = GlobalSearch('Display','iter');

再現性を確保するために、乱数ジェネレータのシードを設定します。

rng(14,'twister')

ソルバーを実行します。

[x,fval] = run(gs,problem)

 Num Pts                 Best       Current    Threshold        Local        Local                 
Analyzed  F-count        f(x)       Penalty      Penalty         f(x)     exitflag        Procedure
       0      200       555.6                                   555.6            0    Initial Point
     200     1463   1.547e-15                               1.547e-15            1    Stage 1 Local
     300     1564   1.547e-15     5.858e+04        1.074                              Stage 2 Search
     400     1664   1.547e-15      1.84e+05         4.16                              Stage 2 Search
     500     1764   1.547e-15     2.683e+04        11.84                              Stage 2 Search
     600     1864   1.547e-15     1.122e+04        30.95                              Stage 2 Search
     700     1964   1.547e-15     1.353e+04        65.25                              Stage 2 Search
     800     2064   1.547e-15     6.249e+04        163.8                              Stage 2 Search
     900     2164   1.547e-15     4.119e+04        409.2                              Stage 2 Search
     950     2359   1.547e-15           477        589.7          387            2    Stage 2 Local
     952     2423   1.547e-15         368.4          477        250.7            2    Stage 2 Local
    1000     2471   1.547e-15     4.031e+04        530.9                              Stage 2 Search

GlobalSearch stopped because it analyzed all the trial points.

3 out of 4 local solver runs converged with a positive local solver exit flag.

x = 1×2
10-7 ×

    0.0414    0.1298

fval = 
1.5467e-15

ソルバーは、[0,0]付近の大域的最小値を含む3つのローカル最小値を見つけます。

MultiStart による多重極小値

MultiStart を使用して複数の最小値を探索するには、まず問題構造を作成します。この問題には制約がないため、fminunc ソルバーを使用します。コマンドラインに何も表示しないようにオプションを設定します。

problem = createOptimProblem('fminunc',...
    'objective',@(x)sawtoothxy(x(1),x(2)),...
    'x0',[100,-50],'options',...
    optimoptions(@fminunc,'Display','off'));

問題の構造を実行して検証します。

[x,fval] = fminunc(problem)

x = 1×2

    8.4420 -110.2602

fval = 
435.2573

デフォルトの MultiStart オブジェクトを作成します。

ms = MultiStart;

ソルバーを 50 回繰り返し実行し、局所的最小値を記録します。

rng(1) % For reproducibility
[x,fval,eflag,output,manymins] = run(ms,problem,50)

MultiStart completed some of the runs from the start points. 

10 out of 50 local solver runs converged with a positive local solver exitflag.

x = 1×2

  -73.8348 -197.7810

fval = 
766.8260

eflag = 
2

output = struct with fields:
                funcCount: 8574
         localSolverTotal: 50
       localSolverSuccess: 10
    localSolverIncomplete: 40
    localSolverNoSolution: 0
                  message: 'MultiStart completed some of the runs from the start points. ↵↵10 out of 50 local solver runs converged with a positive local solver exitflag.'

manymins=1×10 GlobalOptimSolution array with properties:
    X
    Fval
    Exitflag
    Output
    X0

ソルバーは [0,0] 付近の大域的最小値を見つけられません。ソルバーは 10 個の異なる局所最小値を見つけます。

局所最小値における関数の値をプロットします。

histogram([manymins.Fval],10)

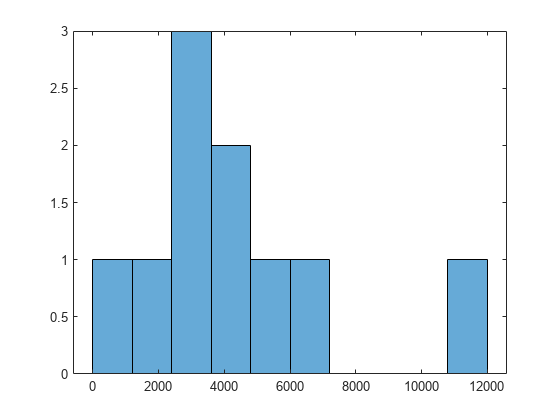
最も良い 3 つのポイントで関数の値をプロットします。

bestf = [manymins.Fval];
histogram(bestf(1:3),10)

MultiStart は、コンポーネントが -1000 から 1000 の間に均一に分布している開始点から fminunc を開始します。fminunc は、多くの局所的最小値の 1 つで頻繁に停止します。fminunc は、反復制限または関数評価制限を 40 回超えます。

参考

GlobalSearch | MultiStart | createOptimProblem

トピック

• GlobalSearchとMultiStartのワークフロー
• 引き込み領域を視覚化する