このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

surrogateopt

時間のかかる目的関数の大域的最小化のためのサロゲート最適化

構文

x = surrogateopt(objconstr,lb,ub)

x = surrogateopt(objconstr,lb,ub,intcon)

x = surrogateopt(objconstr,lb,ub,intcon,A,b,Aeq,beq)

x = surrogateopt(___,options)

x = surrogateopt(problem)

x = surrogateopt(checkpointFile)

x = surrogateopt(checkpointFile,opts)

[x,fval] = surrogateopt(___)

[x,fval,exitflag,output] = surrogateopt(___)

[x,fval,exitflag,output,trials] = surrogateopt(___)

説明

surrogateopt は、時間のかかる目的関数のグローバル ソルバーです。

surrogateoptは次のような形式の問題を解決しようとします。

$$\underset{x}{\min }f(x)\text{ such that }\{\begin{array}{l}\text{lb}\le x\le \text{ub}\\ A·x\le b\\ \text{Aeq}·x=\text{beq}\\ c(x)\le 0\\ x_i\text{ integer, }i\in \text{intcon}\text{.}\end{array}$$

ソルバーは、境界、オプションの線形制約、オプションの整数制約、およびオプションの非線形不等式制約に従って、複数の次元で実数値目的関数の大域的最小値を探索します。surrogateopt は、評価に長い時間を要する目的関数に最適です。目的関数は滑らかでない場合があります。ソルバーはすべての変数に対して有限の境界を必要とします。ソルバーは、オプションでチェックポイント ファイルを維持して、クラッシュや部分的な実行からの回復、または停止条件を満たした後の最適化の継続を可能にすることができます。目的関数 f(x) は空 ([]) になる可能性があり、その場合、surrogateopt はすべての制約を満たす点を見つけようとします。

x = surrogateopt(objconstr,lb,ub) は、領域 lb <= x <= ub 内で objconstr(x) の大域的最小値を探索します。objconstr(x) が構造体を返す場合、surrogateopt は objconstr(x).Ineq <= 0 を条件として objconstr(x).Fval の最小値を探索します。

メモ

追加パラメーターの受け渡し は、必要に応じて目的関数に追加のパラメーターを渡す方法について説明します。

x = surrogateopt(objconstr,lb,ub,intcon) では、intcon にリストされている変数が整数値を取る必要があります。

x = surrogateopt(objconstr,lb,ub,intcon,A,b,Aeq,beq) では、解 x が不等式 A*x <= b と等式 Aeq*x = beq を満たす必要があります。不等式が存在しない場合は A = [] および b = [] と設定してください。同様に、等式が存在しない場合は、Aeq = [] と beq = [] を設定します。

x = surrogateopt(___,options) は、options のオプションを使用して探索手順を変更します。前の構文の任意の入力引数の組み合わせの後に options を指定します。

x = surrogateopt(problem) は、problem で説明されている構造である problem の最小値を探索します。

x = surrogateopt(checkpointFile) は、保存されたチェックポイント ファイルの状態から最適化の実行を継続します。チェックポイントファイルの操作を参照してください。

x = surrogateopt(checkpointFile,opts) は保存されたチェックポイント ファイルの状態から最適化の実行を継続し、checkpointFile のオプションを opts のオプションに置き換えます。チェックポイントファイルを参照してください。

[x,fval] = surrogateopt(___) は、前の構文のいずれかの入力引数の組み合わせを使用して、ソルバーによって検出された目的関数の最良 (最小) 値も返します。

[x,fval,exitflag,output] = surrogateopt(___) は、ソルバーが停止した理由を説明する整数である exitflag と、最適化手順を説明する構造体である output も返します。

[x,fval,exitflag,output,trials] = surrogateopt(___) は、評価されたすべてのポイントとそれらのポイントにおける目的関数の値を含む構造体も返します。

例

大域的最小値の探索

領域 -2.1 <= x(i) <= 2.1 内の 6 つの山を持つキャメル バック関数の最小値を探索します。この関数には、目的関数値が -1.0316284... である 2 つの大域的最小値と、より高い目的関数値を持つ 4 つのローカル最小値があります。

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
x = surrogateopt(objconstr,lb,ub)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    0.0898   -0.7131

非線形制約のある問題を解く

ローゼンブロック関数の最小値を求める

$$100(x(2)-x(1{)}^2{)}^2+(1-x(1){)}^2$$

解は点[1/3,1/3]の周りの半径1/3の円板上に存在するという非線形制約に従う。

$$(x(1)-1/3{)}^2+(x(2)-1/3{)}^2\le (1/3{)}^2$$.

これを行うには、構造体フィールド Fval に Rosenbrock 関数の値を返し、構造体フィールド Ineq に $$c(x)\le 0$$ の形式で非線形制約値を返す関数 objconstr (x) を記述します。

type objconstr

function f = objconstr(x)
f.Fval = 100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;
f.Ineq = (x(1)-1/3)^2 + (x(2)-1/3)^2 - (1/3)^2;

各コンポーネントの下限を 0、上限を 2/3 にして surrogateopt を呼び出します。

lb = [0,0];
ub = [2/3,2/3];
[x,fval,exitflag] = surrogateopt(@objconstr,lb,ub)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    0.6546    0.4277

fval = 
0.1194

exitflag = 
0

解における非線形制約の値を確認します。

disp(objconstr(x).Ineq)

   9.9334e-04

制約関数の値はゼロに近く、解において制約がアクティブであることを示します。

混合整数問題を解く

最初の要素が整数値に制限され、すべての要素が -5 から 5 までの範囲にある 2 次元変数 x の ps_example 関数の最小値を求めます。

intcon = 1;
rng default % For reproducibility
objconstr = @ps_example;
lb = [-5,-5];
ub = [5,5];
x = surrogateopt(objconstr,lb,ub,intcon)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

   -5.0000    0.0004

デフォルト以外のオプションを使用したサロゲート最適化

領域 -2.1 <= x(i) <= 2.1 内の 6 つの山を持つキャメル バック関数を最小化します。この関数には、目的関数値が -1.0316284... である 2 つの大域的最小値と、より高い目的関数値を持つ 4 つのローカル最小値があります。

地域を体系的に探索するには、開始点の規則的なグリッドを使用します。関数評価の最大回数を 120 に設定します。'surrogateoptplot' プロット関数を使用します。'surrogateoptplot' プロットを理解するには、surrogateoptplotを解釈する を参照してください。

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
[Xpts,Ypts] = meshgrid(-3:3);
startpts = [Xpts(:),Ypts(:)];
options = optimoptions('surrogateopt','PlotFcn','surrogateoptplot',...
    'InitialPoints',startpts,'MaxFunctionEvaluations',120);
x = surrogateopt(objconstr,lb,ub,options)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    0.0900   -0.7125

surrogateopt における線形制約

線形不等式制約に従って非線形目的関数を最小化します。200 回の関数評価を最小化します。

objconstr = @multirosenbrock;
nvar = 6;
lb = -2*ones(nvar,1);
ub = -lb;
intcon = [];
A = ones(1,nvar);
b = 3;
Aeq = [];
beq = [];
options = optimoptions('surrogateopt','MaxFunctionEvaluations',200);
[sol,fval,exitflag,output] = ...
    surrogateopt(objconstr,lb,ub,intcon,A,b,Aeq,beq,options)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

sol = 1×6

    0.2072    0.0437    0.1360    0.0066    0.1196   -0.0002

fval = 
2.1853

exitflag = 
0

output = struct with fields:
        elapsedtime: 30.3115
          funccount: 200
    constrviolation: 0
               ineq: [1×0 double]
           rngstate: [1×1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'

問題構造のサロゲート最適化

領域 -2.1 <= x(i) <= 2.1 内の 6 つのこぶを持つキャメルバック関数を表す問題構造を作成します。関数評価の最大回数を 120 に設定します。

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
options = optimoptions('surrogateopt','MaxFunctionEvaluations',120);
problem = struct('objective',objconstr,...
    'lb',[-2.1,-2.1],...
    'ub',[2.1,2.1],...
    'options',options,...
    'solver','surrogateopt');
x = surrogateopt(problem)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    0.0898   -0.7131

サロゲート最適化目的関数の値を返す

6 つのこぶを持つキャメルバック関数を最小化し、最小化点と目的関数の値の両方を返します。他のすべての表示を抑制するオプションを設定します。

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
options = optimoptions('surrogateopt','Display','off','PlotFcn',[]);
[x,fval] = surrogateopt(objconstr,lb,ub,options)

x = 1×2

    0.0898   -0.7131

fval = 
-1.0316

サロゲート最適化プロセスの監視

surrogateopt にさらに多くの出力を返すように要求して、サロゲート最適化プロセスを監視します。'surrogateoptplot' プロット関数を使用します。'surrogateoptplot' プロットを理解するには、surrogateoptplotを解釈する を参照してください。

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
options = optimoptions('surrogateopt','PlotFcn','surrogateoptplot');
[x,fval,exitflag,output] = surrogateopt(objconstr,lb,ub,options)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    0.0898   -0.7131

fval = 
-1.0316

exitflag = 
0

output = struct with fields:
        elapsedtime: 13.2674
          funccount: 200
    constrviolation: 0
               ineq: [1×0 double]
           rngstate: [1×1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'

サロゲート最適化を再開する

関数評価の最大数を小さく設定することで、サロゲート最適化を迅速に完了します。最適化を再開する可能性に備えて、すべてのソルバーの出力を要求。

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
options = optimoptions('surrogateopt','MaxFunctionEvaluations',20);
[x,fval,exitflag,output,trials] = surrogateopt(objconstr,lb,ub,options);

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

以前評価したポイントから始めて、さらに 20 回の関数評価を最適化します。

options.InitialPoints = trials;
[x,fval,exitflag,output,trials] = surrogateopt(objconstr,lb,ub,options);

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

これら 40 個の関数評価のプロットを 大域的最小値の探索 のプロットと比較すると、サロゲート最適化を再開することは、ソルバーを継続的に実行することと同じではないことがわかります。

チェックポイントファイルからサロゲート最適化を再開する

クラッシュやその他の理由によりサロゲート最適化を再開できるようにするには、チェックポイント ファイル名を設定します。

opts = optimoptions('surrogateopt','CheckpointFile','checkfile.mat');

最適化問題を作成し、少数の関数評価を設定します。

rng default % For reproducibility
objconstr = @(x)(4*x(:,1).^2 - 2.1*x(:,1).^4 + x(:,1).^6/3 ...
    + x(:,1).*x(:,2) - 4*x(:,2).^2 + 4*x(:,2).^4);
lb = [-2.1,-2.1];
ub = -lb;
opts.MaxFunctionEvaluations = 30;
[x,fval,exitflag,output] = surrogateopt(objconstr,lb,ub,opts)

Surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    0.0067   -0.7343

fval = -0.9986

exitflag = 0

output = struct with fields:
        elapsedtime: 28.7221
          funccount: 30
    constrviolation: 0
               ineq: [1×0 double]
           rngstate: [1×1 struct]
            message: 'Surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'

オプションを設定して、100 回の関数評価 (すでに実行されたものより 70 回多い) を実行し、最適化を再開します。

opts.MaxFunctionEvaluations = 100;
[x2,fval2,exitflag2,output2] = surrogateopt('checkfile.mat',opts)

Surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x2 = 1×2

    0.0895   -0.7130

fval2 = -1.0316

exitflag2 = 0

output2 = struct with fields:
        elapsedtime: 159.2411
          funccount: 100
    constrviolation: 0
               ineq: [1×0 double]
           rngstate: [1×1 struct]
            message: 'Surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'

入力引数

objconstr — 目的関数と非線形制約

関数ハンドル | 関数名

目的関数と非線形制約。関数ハンドルまたは関数名として指定されます。objconstr は単一の引数 x を受け入れます。ここで、x は通常、行ベクトルです。ただし、Vectorized オプションが true の場合、x は options.BatchUpdateInterval 行を含む行列になり、各行は評価する 1 つのポイントを表します。objconstr は次のいずれかを返します。

• 実数スカラー fval = objconstr(x)。

• 構造。構造体にフィールド Fval が含まれている場合、surrogateopt は objconstr(x).Fval を最小化しようとします。構造体にフィールド Ineq が含まれている場合、surrogateopt はそのフィールドのすべてのコンポーネントを非正にしようとします。つまり、すべてのエントリに対して objconstr(x).Ineq <= 0 になります。objconstr(x) には、Fval フィールドまたは Ineq フィールドのいずれか、またはその両方が含まれている必要があります。surrogateopt は他のフィールドを無視します。制約がない場合は、objconstr(x).Ineq フィールドを設定しないでください。また、objconstr(x).Ineq を NaN ではなく [] に設定してください。

Vectorized オプションが true で、BatchUpdateInterval が 1 より大きい場合、objconstr は x の各行を操作し、次のいずれかを返します。

• 実数ベクトル fval = objconstr(x)。fval は、options.BatchUpdateInterval 個のエントリを持つ列ベクトルです (BatchUpdateInterval が MaxFunctionEvaluations を均等に割り切れない場合は、最後の関数評価ではエントリ数が少なくなります)。

• ベクトルエントリを持つ構造体。構造体にフィールド Fval が含まれている場合、surrogateopt は objconstr(x).Fval を最小化しようとし、objconstr(x).Fval は長さ BatchUpdateInterval (またはそれ以下) のベクトルになります。構造体にフィールド Ineq が含まれている場合、surrogateopt はそのフィールドのすべてのコンポーネントを非正にしようとします。つまり、すべてのエントリに対して objconstr(x).Ineq <= 0 となり、objconstr(x).Ineq には最大 BatchUpdateInterval エントリが含まれます。

目的関数 objconstr.Fval は空 ([]) になる可能性があり、その場合、surrogateopt はすべての制約を満たす点を見つけようとします。実現可能性問題を解決するを参照してください。

非線形制約を使用する例については、非線形制約のある問題を解く、非線形制約によるサロゲート最適化、および 実現可能性問題を解決する を参照してください。surrogateopt 構造構文と他のソルバー間の変換については、packfcn および 非線形制約を surrogateopt 形式と他のソルバー形式の間で変換する を参照してください。ベクトル化されたバッチ評価を使用する例については、Simulink モデルを並列に最適化 を参照してください。

データ型: function_handle | char | string

lb — 下限

有限実ベクトル

下限は有限の実数ベクトルとして指定されます。lb は、lb ≤ x ≤ ub の要素ごとに下限を表します。lb と ub の長さは、objconstr が受け入れる変数の数と等しくなければなりません。

注意

lb はほとんどのソルバーではオプションですが、surrogateopt では lb は必須の入力です。

メモ

surrogateopt は、lb と ub に等しいエントリを許可します。intcon 内の各 i に対して、ceil(lb(i)) <= floor(ub(i)) が必要です。サロゲートの詳細を構築するを参照してください。

例: lb = [0;-20;4] は x(1) ≥ 0、x(2) ≥ -20、x(3) ≥ 4 を意味します。

データ型: double

ub — 上限

有限実ベクトル

上限は有限の実数ベクトルとして指定されます。ub は、lb ≤ x ≤ ub 内の要素ごとの上限を表します。lb と ub の長さは、objconstr が受け入れる変数の数と等しくなければなりません。

注意

ub はほとんどのソルバーではオプションですが、surrogateopt では ub は必須の入力です。

メモ

surrogateopt は、lb と ub に等しいエントリを許可します。intcon 内の各 i に対して、ceil(lb(i)) <= floor(ub(i)) が必要です。サロゲートの詳細を構築するを参照してください。

例: ub = [10;-20;4] は x(1) ≤ 10、x(2) ≤ -20、x(3) ≤ 4 を意味します。

データ型: double

intcon — 整数変数

正の整数のベクトル

整数変数。1 から問題の変数の数までの値を持つ正の整数のベクトルとして指定されます。intcon の各値は、整数値の x コンポーネントを表します。

例: x 内の偶数エントリが整数値であることを指定するには、intcon を 2:2:nvars に設定します。

データ型: double

A — 線形不等式制約

実数行列

線形不等式制約。実数行列として指定されます。A は M 行 nvars 列の行列で、M は不等式の数です。

A は M 個の線形不等式を符号化します。

A*x <= b,

ここで、x は nvars 個の変数 x(:) の列ベクトル、b は M 個の要素をもつ列ベクトルです。

例えば、

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

次の制約を与えます:

A = [1,2;3,4;5,6];
b = [10;20;30];

例: 制御変数の合計が 1 以下になるように指定するには、制約 A = ones(1,N) と b = 1 を指定します。

データ型: double

b — 線形不等式制約

実数ベクトル

実数ベクトルで指定される線形不等式制約です。b は、行列 A に関連する M 要素ベクトルです。b を行ベクトルとして渡す場合、ソルバーは b を列ベクトル b(:) に内部的に変換します。

b は M 個の線形不等式を符号化します。

A*x <= b,

ここで、x は N 個の変数 x(:) の列ベクトル、A は M 行 N 列の行列です。

例えば、

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

次の制約を与えます:

A = [1,2;3,4;5,6];
b = [10;20;30];

例: 制御変数の合計が 1 以下になるように指定するには、制約 A = ones(1,N) と b = 1 を指定します。

データ型: double

Aeq — 線形等式制約

実数行列

線形等式制約。実数行列として指定されます。Aeq は Me 行 nvars 列の行列で、Me は等式の数です。

Aeq は Me 個の線形等式を符号化します。

Aeq*x = beq,

ここで、x は N 個の変数 x(:) の列ベクトル、beq は Me 個の要素をもつ列ベクトルです。

例えば、

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

次の制約を与えます:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

例: 制御変数の合計が 1 になるように指定するには、制約 Aeq = ones(1,N) と beq = 1 を指定します。

データ型: double

beq — 線形等式制約

実数ベクトル

実数ベクトルで指定される線形等式制約です。beq は、行列 Aeq に関連する Me 要素ベクトルです。beq を行ベクトルとして渡す場合、ソルバーは beq を列ベクトル beq(:) に内部的に変換します。

beq は Me 個の線形等式を符号化します。

Aeq*x = beq,

ここで、x は N 個の変数 x(:) の列ベクトル、Aeq は Meq 行 N 列の行列です。

例えば、

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

次の制約を与えます:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

例: 制御変数の合計が 1 になるように指定するには、制約 Aeq = ones(1,N) と beq = 1 を指定します。

データ型: double

options — オプション

optimoptions の出力

optimoptions の出力として指定されるオプション。

詳細については、サロゲート最適化オプションを参照してください。

オプション	説明	値
BatchUpdateInterval	サロゲートが更新される前の関数評価の回数。 ベクトル化された評価で渡すポイントの数。UseVectorized が true の場合、surrogateopt はサイズが BatchUpdateInterval 行 nvar 列の行列を渡します。ここで、nvar は問題の変数の数です。行列の各行は 1 つの評価ポイントを表します。各バッチが完全に評価された後、出力関数とプロット関数が更新されます。	正の整数。既定値は 1 です。
CheckpointFile	チェックポイントと最適化の再開のためのファイル名。ファイルのデータ型は .mat です。チェックポイントファイルの操作を参照してください。 チェックポイント作成には時間がかかります。このオーバーヘッドは、評価にほとんど時間がかからない関数の場合に特に顕著になります。	文字列または文字配列として指定されるファイル名またはファイル パス。パスなしでファイル名を指定すると、surrogateopt はチェックポイント ファイルを現在のフォルダーに保存します。
ConstraintTolerance	非線形制約の許容範囲。すべての非線形制約関数値の最大値として測定され、正の値は違反を示します。この許容差は絶対的な（相対的ではない）許容差です。許容誤差と停止条件 を参照してください。	非負のスカラー。既定値は 1e-3 です。
Display	コマンド ラインで返される表示レベル。	'final' (デフォルト) — 反復処理の終了時の終了メッセージ。 'off' または同等の 'none' — 表示されません。 'iter' — 反復表示。コマンド ラインの表示 を参照してください。
InitialPoints	ソルバーの初期点。	初期点の行列。各行は 1 つの点です。または、値が初期点の行列であるフィールド X と、次のオプション フィールドを持つ構造体: Fval、初期点における目的関数の値を含むベクトル Ineq、非線形不等式制約値を含む行列 アルゴリズム制御を参照してください。既定値は [] です。
MaxFunctionEvaluations	目的関数評価の最大数、停止基準。	非負の整数。デフォルトは max(200,50*nvar) です。ここで、nvar は問題変数の数です。
MaxTime	最大実行時間（秒）。実際の実行時間は、目的関数の評価に必要な時間や並列処理の遅延により、MaxTime を超える場合があります。	非負のスカラー。既定値は Inf です。
MinSampleDistance	適応サンプラーによって生成された試行ポイント間の最小距離。サロゲート最適化アルゴリズムを参照してください。	非負のスカラー。既定値は 1e-6 です。
MinSurrogatePoints	サロゲート作成フェーズの開始時に作成するランダム サンプル ポイントの最小数。サロゲート最適化アルゴリズムを参照してください。 BatchUpdateInterval > 1 の場合、サロゲートを作成するために使用されるランダム サンプル ポイントの最小数は、 MinSurrogatePoints と BatchUpdateInterval のうち大きい方になります。	少なくとも nvar + 1 の整数。デフォルトは max(20,2*nvar) です。ここで、nvar は問題変数の数です。
ObjectiveLimit	目的関数の値に対する許容範囲。実行可能なポイントの計算された目的関数の値が ObjectiveLimit 未満の場合、アルゴリズムは停止します。	double スカラー値。既定値は -Inf です。
OutputFcn	ソルバーの進行状況を報告したり、ソルバーを停止したりするための出力関数。出力関数を参照してください。	関数名、関数ハンドル、または関数名またはハンドルのセル配列。既定値は [] です。
PlotFcn	ソルバーの進行状況を表示したり、ソルバーを停止したりするためのプロット関数。プロット関数を参照してください。	関数名、関数ハンドル、または関数名またはハンドルのセル配列。組み込みのプロット関数は次のとおりです。 'optimplotfvalconstr' (デフォルト) — 見つかった最適な実行可能な目的関数の値を折れ線グラフとしてプロットします。目的関数がない場合は、最大非線形制約違反を折れ線グラフとしてプロットします。 プロットでは、実行不可能なポイントが 1 つの色で表示され、実行可能なポイントが別の色で表示されます。 目的関数がない場合、プロットのタイトルには実行可能解の数が表示されます。 'optimplotfval' — 見つかった最適な目的関数の値を折れ線グラフとしてプロットします。 'optimplotx' — 見つかった最適なソリューションを棒グラフとしてプロットします。 'surrogateoptplot' — 各反復における目的関数の値をプロットし、アルゴリズムのどのフェーズで値が生成されたか、およびこのフェーズと全体の両方で見つかった最良の値を表示します。surrogateoptplotを解釈するを参照してください。
UseParallel	目的関数の値を並列に計算するかどうかを示すブール値。 UseParallel = true と UseVectorized = true の両方を指定することはできません。両方を true に設定すると、ソルバーは UseVectorized を無視し、可能な場合は並列プールを使用して並列計算を試みます。	ブール値。既定値は false です。アルゴリズムの詳細については、並列surrogateoptアルゴリズム を参照してください。
UseVectorized	目的関数の値をサイズ BatchUpdateInterval のバッチで計算するかどうかを示すブール値。 UseParallel = true と UseVectorized = true の両方を指定することはできません。両方を true に設定すると、ソルバーは UseVectorized を無視し、可能な場合は並列プールを使用して並列計算を試みます。	ブール値。既定値は false です。例については、Simulink モデルを並列に最適化を参照してください。

例: options = optimoptions('surrogateopt','Display','iter','UseParallel',true)

problem — 問題構造体

構造体

問題構造体。次のフィールドをもつ構造体を指定します。

• objective — 関数名または関数ハンドルとして指定される、非線形制約を含むことができる目的関数

• lb — x の下限

• ub — x の上限

• solver — 'surrogateopt'

• Aineq — 線形不等式制約の行列（オプション）

• bineq — 線形不等式制約のベクトル（オプション）

• Aeq — 線形等式制約の行列（オプション）

• beq — 線形等式制約のベクトル（オプション）

• options — optimoptions で作成されたオプション

• rngstate — 乱数ジェネレーターの状態をリセットするフィールド（オプション）

• intcon — 整数値のxコンポーネントを指定するフィールド（オプション）

メモ

これらの problem フィールドは必須です: objective、lb、ub、solver、および options。

データ型: struct

checkpointFile — チェックポイントファイルへのパス

string | 文字ベクトル

文字列または文字ベクトルとして指定されたチェックポイント ファイルへのパス。チェックポイント ファイルには .mat 拡張子が付きます。パスなしでファイル名を指定すると、surrogateopt は現在のフォルダー内のチェックポイント ファイルを使用します。

チェックポイント ファイルには、最適化を再開するための最適化の状態が保存されます。surrogateopt は関数評価ごとにチェックポイント ファイルを更新するため、surrogateopt が途中で停止した場合でも最適化を再開できます。例については、チェックポイントファイルからサロゲート最適化を再開するを参照してください。

surrogateopt は、有効な CheckpointFile オプションがある場合にチェックポイント ファイルを作成します。

チェックポイント ファイルから再開するときに、いくつかのオプションを変更できます。optsを参照してください。

チェックポイント ファイル内のデータは .mat 形式です。エラーやその他の予期しない結果を回避するには、surrogateopt を呼び出す前にデータを変更しないでください。

警告

異なる MATLAB^® バージョンで作成されたチェックポイント ファイルから surrogateopt を再開しないでください。surrogateopt はエラーをスローしたり、矛盾した結果を返したりする可能性があります。

例: 'checkfile.mat'

例: "C:\Program Files\MATLAB\docs\checkpointNov2019.mat"

データ型: char | string

opts — チェックポイントファイルから再開するためのオプション

[] (既定値) | 制限されたセットからのoptimoptionsオプション

チェックポイント ファイルから最適化を再開するためのオプション。元のオプションから変更できる optimoptions オプション (制限されたセットから) として指定されます。変更できるオプションは次のとおりです。

• BatchUpdateInterval

• CheckpointFile

• Display

• MaxFunctionEvaluations

• MaxTime

• MinSurrogatePoints

• ObjectiveLimit

• OutputFcn

• PlotFcn

• UseParallel

• UseVectorized

例: opts = optimoptions(options,'MaxFunctionEvaluations',400);

出力引数

x — 解

実数ベクトル

解は実数ベクトルとして返されます。x は、lb および ub と同じ長さです。

fval — 解での目的関数値

実数

解での目的関数値。実数として返されます。

• objconstr がスカラーを返す場合、fval はスカラー objconstr(x) です。

• objconstr が構造体を返す場合、fval は値 objconstr(x).Fval、つまり x における目的関数の値 (この値が存在する場合) です。

exitflag — surrogateopt の停止理由

整数

surrogateopt が停止した理由は、この表で説明されている整数値の 1 つとして返されます。

終了フラグ	説明
10	次のいずれかの理由により、問題に固有の実行可能解があることを示します。 すべての上限 ub が下限 lb に等しい。 線形等式制約 Aeq*x = beq と範囲に固有の解の点がある。 surrogateopt は、最適化を実行することなく実行可能点と関数値を返します。
3	実行可能点が検出されたことを示します。検出された新しい実行可能点が少なすぎて続行不可能なため、ソルバーが停止しました。
1	目的関数値が options.ObjectiveLimit より小さくなっていることを示します。この終了フラグは終了フラグ 10 よりも優先されます (どちらも該当する場合)。
0	関数評価の回数が options.MaxFunctionEvaluations を超過、または経過時間が options.MaxTime を超過したことを示しています。問題に非線形不等式が含まれている場合、解は実行可能です。
-1	出力関数またはプロット関数によって最適化が停止したことを示します。
-2	次のいずれかの理由により、実行可能点が検出されなかったことを示します。 下限 lb(i) が対応する上限 ub(i) を超えている。または、1 つ以上の ceil(lb(i)) が、intcon の i について、対応する floor(ub(i)) を超えている。この場合、surrogateopt は x = [] および fval = [] を返します。 lb = ub および点 lb が実行不可能である。この場合、x = lb および fval = objconstr(x).Fval です。 線形制約および整数制約 (存在する場合) が境界と共に実行不可能である。この場合、surrogateopt は x = [] および fval = [] を返します。 範囲制約、整数制約および線形制約が実行可能であるが、非線形制約で実行可能解が検出されない。この場合、x は非線形制約で最小の最大実行不可能点であり、fval = objconstr(x).Fval となります。

output — 最適化プロセスに関する情報

構造体

最適化プロセスに関する情報。次のフィールドをもつ構造体として返されます。

• funccount — 関数評価の合計回数。

• elapsedtime — tic/toc で測定された、ソルバーの実行に費やされた時間（秒）。

• message — アルゴリズムが停止した理由。

• constrviolation — 最大非線形制約違反（存在する場合）。constrviolation = max(output.ineq)。

• ineq — 解 x における非線形不等式制約値。objconstr が構造体を返す場合、ineq = objconstr(x).Ineq になります。それ以外の場合、ineq は空です。

• rngstate — アルゴリズムが開始する直前の MATLAB 乱数ジェネレーターの状態。このフィールドを使用して結果を再現します。ga の代わりに rngstate を使用する方法については、結果を再現する を参照してください。

trials — 評価ポイント

構造体

評価されたポイントは、次のフィールドを持つ構造体として返されます。

• X — nvars 列の行列。ここで、nvars は lb または ub の長さです。X の各行は、surrogateopt によって評価される 1 つのポイントを表します。

• Fval — 列ベクトル。各エントリは、X の対応する行の目的関数の値です。

• Ineq — 各行が X の対応する行の制約関数の値を表す行列。

trials 構造は options.InitialPoints 構造と同じ形式です。したがって、trials 構造を InitialPoints オプションとして渡すことで最適化を続行できます。

アルゴリズム

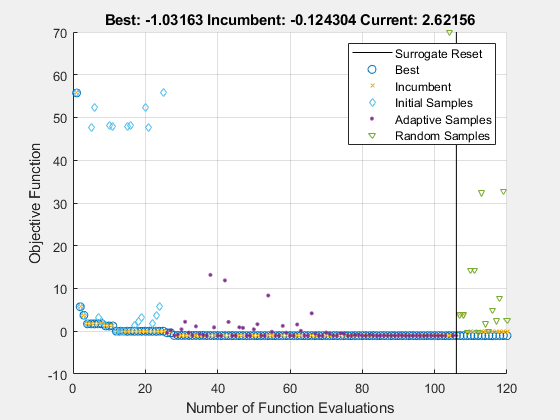
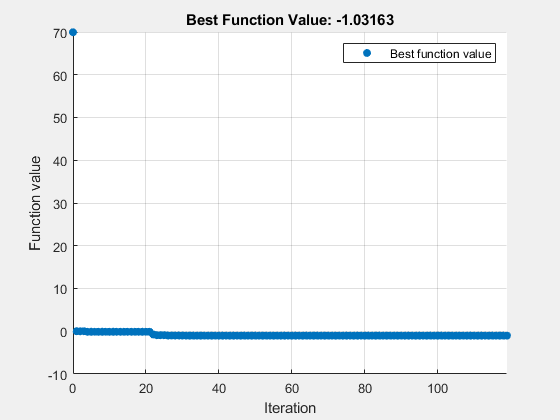
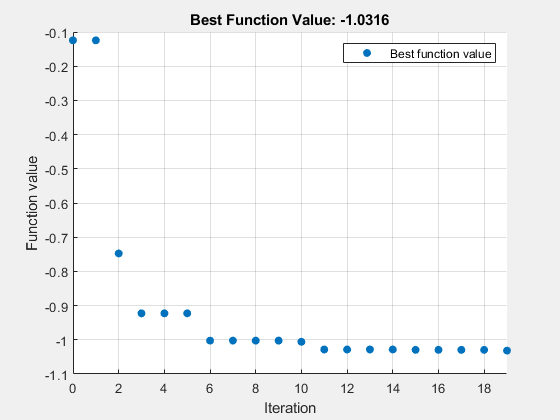
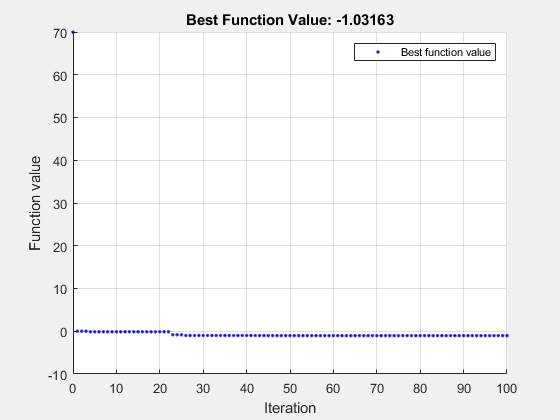
surrogateopt は次の手順を繰り返し実行します。

1. 境界内で MinSurrogatePoints 個のランダム ポイントをサンプリングして試行ポイントのセットを作成し、試行ポイントで目的関数を評価します。

2. すべてのランダム試行ポイントを通るラジアル基底関数を補間することにより、目的関数のサロゲート モデルを作成します。

3. サロゲートにいくらかの重みを与え、試行ポイントからの距離にいくらかの重みを与えるメリット関数を作成します。現行ポイント（最後のサロゲート リセット以降に見つかった最良のポイント）の周囲の領域でメリット関数をランダムにサンプリングして、メリット関数の小さな値を見つけます。適応ポイントと呼ばれるこの点を、新しい試行ポイントとして使用します。

4. 適応ポイントで目的を評価し、この点とその値に基づいてサロゲートを更新します。目的関数の値が、以前に観測された最高（最低）値よりも十分に低い場合は「成功」とカウントし、そうでない場合は「失敗」とカウントします。

5. max(nvar,5) 回の失敗の前に 3 回の成功が発生した場合、サンプル分布の分散を上方に更新します。ここで、nvar は次元数です。3 回の成功の前に max(nvar,5) 回の失敗が発生した場合は、分散を下方に更新します。

6. すべての試行ポイントが評価ポイントの MinSampleDistance 以内になるまで、手順 3 から続行します。その時点で、サロゲートからすべての適応ポイントを破棄してサロゲートをリセットし、スケールをリセットして、ステップ 1 に戻り、評価用の MinSurrogatePoints 個の新しいランダム試行ポイントを作成します。

詳細は、サロゲート最適化アルゴリズムを参照してください。

代替機能

アプリ

[最適化] ライブ エディター タスクが surrogateopt にビジュアル インターフェイスを提供します。

拡張機能

自動並列サポート

Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

並列実行するには、'UseParallel' オプションを true に設定します。

options = optimoptions('solvername','UseParallel',true)

詳細については、Global Optimization Toolbox で並列処理を使用する方法を参照してください。

バージョン履歴

R2018b で導入

R2024a: surrogateoptアルゴリズムの効率が向上

surrogateopt は、特に整数制約の問題に対して効率性を向上させる内部ルーチンを更新しました。また、高速な目的関数と非線形制約関数を持つ問題の場合、チェックポイントは以前よりも効率的です。surrogateopt は、10 秒間に 1 回しかチェックポイント ファイルを書き込みません。詳細については、サロゲート最適化アルゴリズムとチェックポイントファイルを参照してください。

参考

patternsearch | optimoptions | packfcn | 最適化

トピック

• サロゲート最適化
• 大域的最適解と局所的最適解
• 混合整数ga最適化
• サロゲート最適化オプション