このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

非線形制約によるサロゲート最適化

この例では、サロゲート最適化に非線形不等式制約を含める方法を示します。この例では、非線形制約を持つ ODE を解きます。例 並列で常微分方程式を最適化する は、非線形制約を受け入れる他のソルバーを使用して同じ問題を解決する方法を示しています。

この例のビデオ概要については、サロゲート最適化 を参照してください。

問題の説明

問題は、大砲の位置と角度を変えて、できるだけ壁を越えて弾丸を発射することです。大砲の砲口速度は300m/sです。壁の高さは20メートルです。大砲が壁に近すぎると、発射角度が急になり、発射物が十分遠くまで飛びません。大砲が壁から離れすぎると、発射物は十分な距離まで飛びません。

非線形の空気抵抗により、発射体の速度が低下します。抵抗力は速度の2乗に比例し、比例定数は0.02です。重力は発射体に作用し、一定の 9.81 m/s^2 で下向きに加速します。したがって、軌跡x(t)の運動方程式は

$$\frac{d^{2}x(t)}{d{t}^2}=-0.02\Vert v(t)\Vert v(t)-(0,9.81),$$

ここで、$$v(t)=dx(t)/dt$$ です。

初期位置 x0 と初期速度 xp0 は 2 次元ベクトルです。ただし、初期の高さ x0(2) は 0 なので、初期位置はスカラー x0(1) によって指定されます。初期速度の大きさは 300 (銃口速度) であるため、スカラーである初期角度のみに依存します。初期角度が th の場合、初期速度は xp0 = 300*(cos(th),sin(th)) です。したがって、最適化問題は 2 つのスカラーのみに依存するため、2 次元の問題になります。水平距離と初期角度を決定変数として使用します。

ODEモデルの定式化

ODE ソルバーでは、モデルを 1 次システムとして定式化する必要があります。軌跡ベクトル $$(x_1(t),x_2(t))$$ にその時間微分 $$(x_1\prime (t),x_2\prime (t))$$ を加えて 4 次元軌跡ベクトルを形成します。この拡大ベクトルに関して、微分方程式は次のようになる。

$$\frac{\mathit{d}}{\mathit{dt}}\mathit{x}\left(\mathit{t}\right)=\left[\begin{array}{c}{\mathit{x}}_3\left(\mathit{t}\right)\\ {\mathit{x}}_4\left(\mathit{t}\right)\\ -0.02\Vert \left({\mathit{x}}_3\left(\mathit{t}\right),{\mathit{x}}_4\left(\mathit{t}\right)\right)\Vert {\mathit{x}}_3\left(\mathit{t}\right)\\ -0.02\Vert \left({\mathit{x}}_3\left(\mathit{t}\right),{\mathit{x}}_4\left(\mathit{t}\right)\right)\Vert {\mathit{x}}_4\left(\mathit{t}\right)-9.81\end{array}\right].$$

cannonshot ファイルはこの微分方程式を実装します。

type cannonshot

function f = cannonshot(~,x)

f = [x(3);x(4);x(3);x(4)]; % initial, gets f(1) and f(2) correct
nrm = norm(x(3:4)) * .02; % norm of the velocity times constant
f(3) = -x(3)*nrm; % horizontal acceleration
f(4) = -x(4)*nrm - 9.81; % vertical acceleration

初期角度 pi/3 で壁から 30 m 離れたところから始まるこの ODE の解を視覚化します。plotcannonsolution 関数は ode45 を使用して微分方程式を解きます。

type plotcannonsolution

function dist = plotcannonsolution(x)
% Change initial 2-D point x to 4-D x0
x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];
sol = ode45(@cannonshot,[0,15],x0);
% Find the time when the projectile lands
zerofnd = fzero(@(r)deval(sol,r,2),[sol.x(2),sol.x(end)]);
t = linspace(0,zerofnd); % equal times for plot
xs = deval(sol,t,1); % interpolated x values
ys = deval(sol,t,2); % interpolated y values
plot(xs,ys)
hold on
plot([0,0],[0,20],'k') % Draw the wall
xlabel('Horizontal distance')
ylabel('Trajectory height')
ylim([0 100])
legend('Trajectory','Wall','Location','NW')
dist = xs(end);
title(sprintf('Distance %f',dist))
hold off

plotcannonsolution は fzero を使用して、発射体が着地する時間 (つまり、高さが 0) を見つけます。発射体は 15 秒前に着地するため、plotcannonsolution は ODE ソリューションの時間として 15 を使用します。

x0 = [-30;pi/3];
dist = plotcannonsolution(x0);

最適化の準備

初期位置と角度を最適化するには、前のプロット ルーチンと同様の関数を記述します。任意の水平位置と初期角度から始まる軌跡を計算します。

適切な境界制約を含めます。水平位置は 0 より大きくできません。上限を -1 に設定します。同様に、水平位置は -200 未満にすることはできないため、下限を -200 に設定します。初期角度は正でなければならないため、下限を 0.05 に設定します。初期角度は pi/2 を超えてはなりません。上限を pi/2 – 0.05 に設定してください。

lb = [-200;0.05];
ub = [-1;pi/2-.05];

初期位置と角度が与えられた場合に、壁からの結果距離の負の値を返す目的関数を記述します。軌跡が20 未満の高さで壁を横切る場合、軌跡は実行不可能であり、この制約は非線形制約です。cannonobjcon 関数は目的関数の計算を実装します。非線形制約を実装するために、関数は fzero を呼び出して、発射体の x 値がゼロになる時間を見つけます。この関数は、時間 15 以降に発射体の x 値が 0 より大きいかどうかをチェックすることにより、fzero 関数の失敗の可能性を考慮します。そうでない場合、関数は発射物が壁を通過する時間を見つける手順をスキップします。

type cannonobjcon

function f = cannonobjcon(x)
    % Change initial 2-D point x to 4-D x0
    x0 = [x(1);0;300*cos(x(2));300*sin(x(2))];
    % Solve for trajectory
    sol = ode45(@cannonshot,[0,15],x0);
    % Find time t when trajectory height = 0
    zerofnd = fzero(@(r)deval(sol,r,2),[1e-2,15]);
    % Find the horizontal position at that time
    dist = deval(sol,zerofnd,1);
    % What is the height when the projectile crosses the wall at x = 0?
    if deval(sol,15,1) > 0
        wallfnd = fzero(@(r)deval(sol,r,1),[0,15]);
        height = deval(sol,wallfnd,2);
    else
        height = deval(sol,15,2);
    end
    f.Ineq = 20 - height; % height must be above 20
    % Take negative of distance for maximization
    f.Fval = -dist;
end

すでに 1 つの実行可能な初期軌跡を計算しました。その値を初期点として使用します。

fx0 = cannonobjcon(x0);
fx0.X = x0;

surrogateopt を使って最適化を解く

初期点を使用するには、surrogateopt オプションを設定します。再現性を確保するために、乱数ジェネレータを default に設定します。'surrogateoptplot' プロット関数を使用します。最適化を実行します。'surrogateoptplot' プロットを理解するには、surrogateoptplotを解釈する を参照してください。

opts = optimoptions('surrogateopt','InitialPoints',x0,'PlotFcn','surrogateoptplot');
rng default
[xsolution,distance,exitflag,output] = surrogateopt(@cannonobjcon,lb,ub,opts)

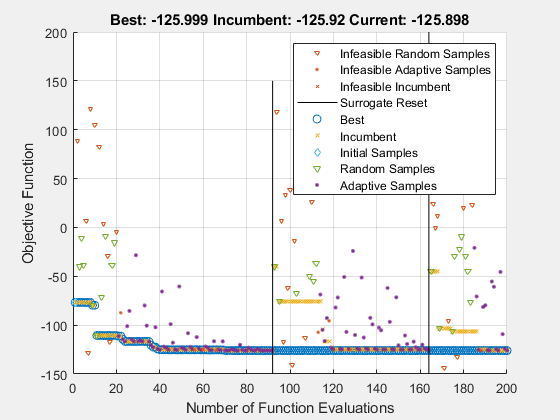
surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

xsolution = 1×2

  -28.4081    0.6160

distance = 
-125.9988

exitflag = 
0

output = struct with fields:
        elapsedtime: 47.0823
          funccount: 200
    constrviolation: 8.4347e-04
               ineq: 8.4347e-04
           rngstate: [1×1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'

最終軌跡をプロットします。

figure
dist = plotcannonsolution(xsolution);

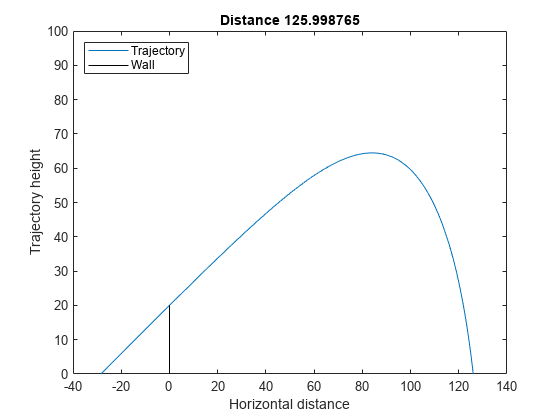
並列で常微分方程式を最適化する の patternsearch ソリューションは最終距離 125.9880 を示しており、これはこの surrogateopt ソリューションとほぼ同じです。

参考

surrogateopt

トピック

• 並列で常微分方程式を最適化する
• サロゲート最適化