optimproblem

最適化問題の作成

構文

prob = optimproblem

prob = optimproblem(Name,Value)

説明

optimproblem を使用して、最適化問題を作成します。

ヒント

完全なワークフローについては、問題ベースの最適化ワークフローを参照してください。

prob = optimproblem は、既定のプロパティで最適化問題を作成します。

prob = optimproblem(Name,Value) は 1 つ以上の Name,Value 引数ペアによって指定された追加オプションを使用します。たとえば、最小化問題の代わりに最大化問題を指定するには、prob = optimproblem('ObjectiveSense','maximize') を使用します。

メモ

最適化問題に含まれるすべての名前は一意でなければなりません。特に、すべての変数名、目的関数名、および制約関数名は異なっている必要があります。

例

最適化問題の作成

既定のプロパティで最適化問題を作成します。

prob = optimproblem

prob = 
  OptimizationProblem with properties:

       Description: ''
    ObjectiveSense: 'minimize'
         Variables: [0×0 struct] containing 0 OptimizationVariables
         Objective: [0×0 OptimizationExpression]
       Constraints: [0×0 struct] containing 0 OptimizationConstraints

  No problem defined.

最大化問題を作成して解く

最大化を目的とする線形計画問題を作成します。問題には、2 つの正の変数と 3 つの線形不等式制約があります。

prob = optimproblem('ObjectiveSense','max');

正の変数を作成します。目的関数を問題に含めます。

x = optimvar('x',2,1,'LowerBound',0);
prob.Objective = x(1) + 2*x(2);

問題の線形不等式制約を作成します。

cons1 = x(1) + 5*x(2) <= 100;
cons2 = x(1) + x(2) <= 40;
cons3 = 2*x(1) + x(2)/2 <= 60;
prob.Constraints.cons1 = cons1;
prob.Constraints.cons2 = cons2;
prob.Constraints.cons3 = cons3;

問題を確認します。

show(prob)

  OptimizationProblem : 

	Solve for:
       x

	maximize :
       x(1) + 2*x(2)


	subject to cons1:
       x(1) + 5*x(2) <= 100

	subject to cons2:
       x(1) + x(2) <= 40

	subject to cons3:
       2*x(1) + 0.5*x(2) <= 60

	variable bounds:
       0 <= x(1)
       0 <= x(2)

問題を解きます。

sol = solve(prob);

Solving problem using linprog.

Optimal solution found.

sol.x

ans = 2×1

    25
    15

多目的問題を作成して解く

2 次元化変数 x の目的関数を 2 つもつ問題を作成します。x の式として目的関数を作成し、それらを構造体として目的に配置します。

x = optimvar("x",2,LowerBound=-2,UpperBound=2);
prob = optimproblem;
prob.Objective.first = norm(x)^2;
prob.Objective.second = norm(x - [1;0])^2;

問題を解きます。

rng default % For reproducibility
sol = solve(prob);

Solving problem using gamultiobj.
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

解をプロットします。

paretoplot(sol)

パレート フロント上の 1 点を検証します。そのためには、Figure をクリックし、データ ヒント ツールをクリックします。

パレート フロント上の点をクリックします。

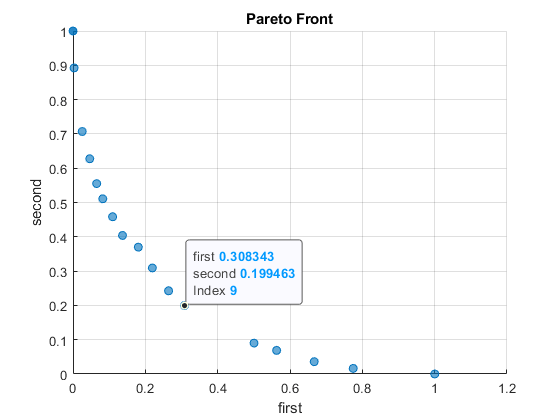
表示された点のインデックスは 9 です。この点に関連付けられた x 値は、インデックス 9 をもつ解として求めることができます。

sol(9).x

ans = 2×1

    0.5544
   -0.0306

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: 最大化問題を指定するには、prob = optimproblem('ObjectiveSense','maximize') を使用します。

Constraints — 問題の制約

OptimizationConstraint 配列 | フィールドとして OptimizationConstraint 配列をもつ構造体

問題の制約。OptimizationConstraint 配列またはフィールドとして OptimizationConstraint 配列をもつ構造体として指定します。

例: prob = optimproblem('Constraints',sum(x,2) == 1)

Description — 問題のラベル

'' (既定値) | string | 文字ベクトル

問題のラベル。string または文字ベクトルとして指定します。Description はソフトウェアでは計算に使用されません。Description は、あらゆる理由で自由に使用できるラベルです。たとえば、モデルまたは問題を共有、アーカイブ、または提示し、モデルまたは問題に関する説明情報を Description に保存できます。

例: "An iterative approach to the Traveling Salesman problem"

データ型: char | string

Objective — 目的関数

スカラー OptimizationExpression | OptimizationExpression の配列 | フィールドとしてスカラー OptimizationExpression をもつ構造体

目的関数。スカラー OptimizationExpression オブジェクト、OptimizationExpression オブジェクトの配列、またはフィールドとしてスカラー OptimizationExpression をもつ構造体として指定します。

• スカラー (単一目的) 問題の場合は、スカラー最適化式として、または値としてスカラー最適化式をもつ構造体として目的関数を指定します。

• 多目的問題の場合は、ベクトル値の最適化式、最適化式の配列、または最適化式の構造体として目的関数を指定します。たとえば、次の目的関数は、スカラー最適化変数 x 内の最適化式の構造体です。

  prob = optimproblem;
  prob.Objective.first = x^2;
  prob.Objective.second = (x + 1)^2;

例: prob = optimproblem('Objective',sum(sum(x))) (2 次元変数 x について)。

例: prob = optimproblem('Objective',(x-a).^2) (x および a のサイズは 2 行 1 列、x は最適化変数)。

ObjectiveSense — 最適化の意味

'minimize' (既定値) | 'min' | 'maximize' | 'max' | フィールドとしてリストされた値をもつ構造体

最適化の意味。'minimize' または 'maximize' で指定します。'min'を指定して 'minimize' を、'max' を指定して 'maximize'を得ることもできます。関数 solve は、ObjectiveSense が 'minimize' の場合に目的関数を最小化し、ObjectiveSense が 'maximize' の場合に目的関数を最大化します。

ObjectiveSense には、値 'minimize'、'min'、'maximize'、または 'max' をもつ構造体を指定できます。この形式は、問題の目的が構造体の場合に使用できます。ObjectiveSense が対応する Objective に適用されるように、Objective 構造体と ObjectiveSense 構造体には同じフィールド名が含まれている必要があります。以下に例を示します。

x = optimvar('x',2,"UpperBound",2,"LowerBound",-2);
prob = optimproblem;
prob.Objective.first = norm(x)^2;
prob.Objective.second = -norm(x - [1;0])^2;
prob.ObjectiveSense.first = "min";
prob.ObjectiveSense.second = "max";

Objective が構造体の場合は、'max' のような名前で ObjectiveSense を指定できます。この場合、すべての目的の ObjectiveSense が同じになります。

例: prob = optimproblem('ObjectiveSense','max')

データ型: char | string

出力引数

prob — 最適化問題

OptimizationProblem オブジェクト

最適化問題。OptimizationProblem オブジェクトとして返されます。通常、問題の説明を完了するには、目的関数と制約を指定します。ただし、目的関数のない実行可能性問題を保持したり制約のない問題を保持したりすることができます。solve を呼び出して、完全な問題を解きます。

警告

問題ベースのアプローチでは、目的関数、非線形等式、および非線形不等式における複素数値はサポートされていません。関数の計算に複素数値が含まれていると、それが中間値としてであっても、最終結果が不正確になる場合があります。

バージョン履歴

R2017b で導入

参考

optimvar | OptimizationProblem | solve

トピック

• 問題ベースの最適化の設定
• 問題ベースの最適化ワークフロー