optimvalues

最適化問題の値の作成

R2022a 以降

構文

val = optimvalues(prob,dataname1,dataval1,...)

説明

val = optimvalues(prob,dataname1,dataval1,...) は、問題 prob の OptimizationValues オブジェクトを作成します。すべての変数名およびそれらに関連付けられた値を指定し、名前と値の引数を使用して、オプションで目的値または制約値を指定します。たとえば、x が 1 ～ 99 の奇数値を取るように指定するには、次のようにします。

val = optimvalues(prob,x=1:2:99);

val は prob の初期点または初期母集団として使用します。

例

問題ベースの ga の初期点の作成

問題ベースのアプローチで ga (遺伝的アルゴリズム ソルバー) の初期点を作成するには、optimvalues を使用して OptimizationValues オブジェクトを作成します。

適応度 (目的) 関数として Rosenbrock 関数をもつ 2 次元問題の最適化変数を作成します。

x = optimvar("x",LowerBound=-5,UpperBound=5);
y = optimvar("y",LowerBound=-5,UpperBound=5);
rosenbrock = (10*(y - x.^2)).^2 + (1-x).^2;
prob = optimproblem(Objective=rosenbrock);

範囲内に 100 個のランダムな 2-D 点を作成します。これらの点は行ベクトルでなければなりません。

rng default % For reproducibility
xval = -5 + 10*rand(1,100);
yval = -5 + 10*rand(1,100);

初期点値オブジェクトを作成します。適応度の値は計算しないため、表示には値が NaN と表示されます。

vals = optimvalues(prob,x=xval,y=yval)

vals = 
  1×100 OptimizationValues vector with properties:

   Variables properties:
            x: [3.1472 4.0579 -3.7301 4.1338 1.3236 -4.0246 -2.2150 0.4688 4.5751 4.6489 -3.4239 4.7059 4.5717 -0.1462 3.0028 -3.5811 -0.7824 4.1574 2.9221 4.5949 1.5574 -4.6429 3.4913 4.3399 1.7874 2.5774 2.4313 -1.0777 1.5548 -3.2881 … ] (1×100 double)
            y: [-3.3782 2.9428 -1.8878 0.2853 -3.3435 1.0198 -2.3703 1.5408 1.8921 2.4815 -0.4946 -4.1618 -2.7102 4.1334 -3.4762 3.2582 0.3834 4.9613 -4.2182 -0.5732 -3.9335 4.6190 -4.9537 2.7491 3.1730 3.6869 -4.1556 -1.0022 -2.4013 … ] (1×100 double)

   Objective properties:
    Objective: [NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN … ] (1×100 double)

ga を使用して問題を解きます。初期点 vals から始めます。ga オプションを設定して 100 個の母集団になるようにします。

opts = optimoptions("ga",PopulationSize=100);
[sol,fv] = solve(prob,vals,Solver="ga",Options=opts)

Solving problem using ga.
ga stopped because it exceeded options.MaxGenerations.

sol = struct with fields:
    x: 1.0551
    y: 1.1133

fv = 
0.0030

ga は、0 付近に適応度値をもつ真の解 x = 1, y = 1 に極めて近い解を返します。

問題ベースの surrogateopt の初期値の作成

問題ベースのアプローチで surrogateopt の初期点を作成するには、optimvalues を使用して OptimizationValues オブジェクトを作成します。

目的関数として Rosenbrock 関数をもつ 2 次元問題の最適化変数を作成します。

x = optimvar("x",LowerBound=-5,UpperBound=5);
y = optimvar("y",LowerBound=-5,UpperBound=5);
rosenbrock = (10*(y - x.^2)).^2 + (1 - x).^2;
prob = optimproblem(Objective=rosenbrock);

解は原点に関して半径 2 の円内で、直線 y = 1 + x より下にあるという制約を作成します。

disc = x^2 + y^2 <= 2^2;
prob.Constraints.disc = disc;
line = y <= 1 + x;
prob.Constraints.line = line;

範囲内に 40 個のランダムな 2-D 点を作成します。これらの点は行ベクトルでなければなりません。

rng default % For reproducibility
N = 40;
xval = -5 + 10*rand(1,N);
yval = -5 + 10*rand(1,N);

ランダムな点上で Rosenbrock 関数を評価します。関数値は行ベクトルでなければなりません。この手順はオプションです。関数値を指定しない場合、surrogateopt は点 (xval,yval) における目的関数を評価します。関数値がある場合は、その値をデータとして指定することによってソルバーの時間を短縮できます。

fval = zeros(1,N);
for i = 1:N
    p0 = struct('x',xval(i),'y',yval(i));
    fval(i) = evaluate(rosenbrock,p0);
end

点について制約を評価します。制約値は行ベクトルでなければなりません。この手順はオプションです。制約値を指定しない場合、surrogateopt は点 (xval,yval) における制約関数を評価します。

discval = zeros(1,N);
lineval = zeros(1,N);
for i = 1:N
    p0 = struct('x',xval(i),'y',yval(i));
    discval(i) = infeasibility(disc,p0);
    lineval(i) = infeasibility(line,p0);
end

初期点値オブジェクトを作成します。

vals = optimvalues(prob,x=xval,y=yval,Objective=fval,disc=discval,line=lineval)

vals = 
  1×40 OptimizationValues vector with properties:

   Variables properties:
            x: [3.1472 4.0579 -3.7301 4.1338 1.3236 -4.0246 -2.2150 0.4688 4.5751 4.6489 -3.4239 4.7059 4.5717 -0.1462 3.0028 -3.5811 -0.7824 4.1574 2.9221 4.5949 1.5574 -4.6429 3.4913 4.3399 1.7874 2.5774 2.4313 -1.0777 1.5548 -3.2881 … ] (1×40 double)
            y: [-0.6126 -1.1844 2.6552 2.9520 -3.1313 -0.1024 -0.5441 1.4631 2.0936 2.5469 -2.2397 1.7970 1.5510 -3.3739 -3.8100 -0.0164 4.5974 -1.5961 0.8527 -2.7619 2.5127 -2.4490 0.0596 1.9908 3.9090 4.5929 0.4722 -3.6138 -3.5071 … ] (1×40 double)

   Objective properties:
    Objective: [1.1067e+04 3.1166e+04 1.2698e+04 1.9992e+04 2.3846e+03 2.6593e+04 2.9811e+03 154.8722 3.5498e+04 3.6362e+04 1.9515e+04 4.1421e+04 3.7452e+04 1.1541e+03 1.6457e+04 1.6510e+04 1.5914e+03 3.5654e+04 5.9109e+03 5.7015e+04 … ] (1×40 double)

   Constraints properties:
         disc: [6.2803 13.8695 16.9638 21.8023 7.5568 12.2078 1.2024 0 21.3146 24.0987 12.7394 21.3751 19.3057 7.4045 19.5331 8.8248 17.7486 15.8313 5.2656 24.7413 4.7390 23.5542 8.1927 18.7982 14.4752 23.7379 2.1343 10.2207 10.7168 … ] (1×40 double)
         line: [0 0 5.3853 0 0 2.9222 0.6709 0 0 0 0.1841 0 0 0 0 2.5648 4.3798 0 0 0 0 1.1938 0 0 1.1217 1.0155 0 0 0 0 0.3467 1.2245 4.3736 0.9735 7.3213 0 0 0 0 3.3884]

surrogateopt を使用して問題を解きます。初期点 vals から始めます。

[sol,fv] = solve(prob,vals,Solver="surrogateopt")

Solving problem using surrogateopt.

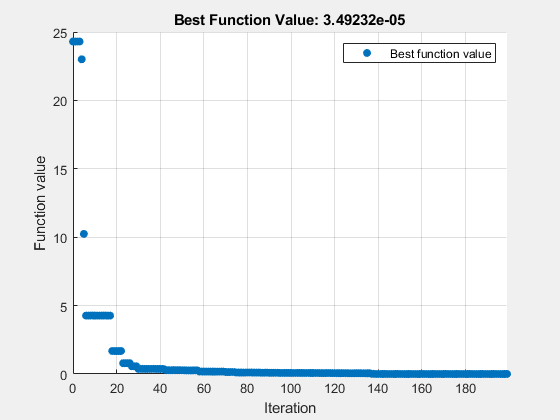
surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

sol = struct with fields:
    x: 1.0031
    y: 1.0057

fv = 
3.4923e-05

surrogateopt は、0 付近に目的関数をもつ真の解 x = 1, y = 1 にある程度近い解を返します。

入力引数

prob — 最適化問題

OptimizationProblem オブジェクト

最適化問題。OptimizationProblem オブジェクトとして指定します。optimproblem を使用して、prob を作成します。

optimvalues から有効な出力を取得するには、名前と値の引数にもデータを含める必要があります。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: val = optimvalues(x=xvals,y=yvals)

dataname — 変数、名前付き目的関数、または名前付き制約のデータ

double の実数配列

変数、名前付き目的関数、または名前付き制約のデータ。double の実数配列として指定します。変数のすべてのデータ名を指定します。目的関数と制約関数の名前はオプションです。

nval 個の点を指定した場合、各 dataname 引数の値は次のような次元になっている必要があります。

prob.property.name	size(value)
スカラーまたはベクトル	numel(prob.property.name) 行 nval 列
行列または配列	size(prob.property.name) 行 nval 列

特に、dataname がベクトルの場合、dataname 引数の値は nval 列の行列です。たとえば、変数 'x' が長さ 2 の行ベクトルで、nval が 3 の場合、変数 'x' の指定は次のようになります。

val = optimvalues(prob,'x',[1 2 3; 4 5 -6]);

このように指定すると、'x' は 3 つの値 [1,4]、[2,5]、および [3,-6] を取るということになります。

例: スカラー 'x' と 2 要素の行ベクトル 'y' (nval = 2: val = optimvalues(prob,x=[5,3],y=[1 2;3 4])) の場合。出力 val の値は x = 5, y = [1 3] および x = 3, y = [2 4] の 2 つとなります。

データ型: double

Objective — 名前のない目的関数の値

double の実数配列

名前のない目的関数の値。double の実数配列として指定します。値のサイズは dataname 内のものと同じです。

最適化問題の多目的関数の値は、2 通りの方法で指定できます。

• 最適化問題の Objective プロパティは関数ハンドルで、この場合は関数がベクトルまたは配列を返します。この場合、行列として値を指定します。行列の各行は、さまざまな点における 1 つの目的関数の値を表します。各列は、1 点におけるさまざまな目的関数の値を表します。

• 最適化問題の Objective プロパティには、複数の名前付き目的関数があります。この場合、各名前付き目的関数の名前を dataname 引数として使用し、その関数の値を指定します。

以下のソルバーは、与えられた任意の目的関数値を使用します。

• ga

• gamultiobj

• paretosearch

• particleswarm

• surrogateopt

例: 1 つの目的関数と 2 つの点 val = optimvalues(prob,x=[3,5],Objective=[exp(3)+1,exp(5)-1]) の場合

データ型: double

Constraints — 名前のない制約関数の値

double の実数

名前のない制約関数の値。double の実数配列として指定します。値のサイズは dataname 内のものと同じです。

最適化問題の複数の制約関数の値は、2 通りの方法で指定できます。

• 最適化問題の Constraints プロパティは関数ハンドルで、この場合は関数が配列を返します。この場合、関数が返すものより 1 つ高い次元の配列として値を指定します。

• 最適化問題の 'Constraints' プロパティには、複数の名前付き制約があります。この場合、各名前付き制約の名前を dataname 引数として使用し、その制約の値を指定します。

以下のソルバーは、与えられた任意の非線形制約関数値を使用します。

• paretosearch

• surrogateopt

以下のソルバーは、すべての反復において、またはすべての母集団メンバーについて線形制約が満たされているかを確認します。

• ga

• gamultiobj

• paretosearch

• patternsearch

• surrogateopt

例: 2 つの点と 3 つの制約 val = optimvalues(prob,x=[3,5],Objective=[exp(3)+1,exp(5)-1],Constraints=[4 5;-7 -2;0.2 12]) の場合

データ型: double

出力引数

val — 点と関数値

OptimizationValues オブジェクトのベクトル

点と関数値。OptimizationValues オブジェクトのベクトルとして返されます。このベクトルには nval 個のエントリがあります。この nval は val 内の点の数です。

バージョン履歴

R2022a で導入

R2023b: particleswarm の初期点と目的関数値の指定

問題ベースのアプローチで particleswarm の初期目的関数値を指定するには、optimvalues を使用します。以下に例を示します。

x = optimvar("x",1,2,LowerBound=[1 2],UpperBound=[11 13]);
fun = sum(exp(x));
prob = optimproblem("Objective",fun);
x0 = [3;5] + 7*rand([2 20]); % Twenty initial points
val = optimvalues(prob,x=x0,Objective=sum(exp(x0),1)); % Twenty initial values
sol = solve(prob,val,Solver="particleswarm")

参考

OptimizationValues

トピック

• 問題ベースのMultiStartの開始点を指定する (Global Optimization Toolbox)
• surrogateopt の開始点と値の指定 (問題ベース) (Global Optimization Toolbox)
• 問題ベースの最適化ワークフロー