Main Content

このページは機械翻訳を使用して翻訳されました。元の英語を参照するには、ここをクリックします。

particleswarm

粒子群最適化法

ページ内をすべて折りたたむ

構文

x = particleswarm(fun,nvars)
x = particleswarm(fun,nvars,lb,ub)
x = particleswarm(fun,nvars,lb,ub,options)
x = particleswarm(problem)
[x,fval,exitflag,output,points] = particleswarm(___)

説明

例

x = particleswarm(fun,nvars) は、 fun の局所最小値を達成するベクトル x を見つけようとします。 nvars は fun の次元 (設計変数の数) です。

メモ

追加パラメーターの受け渡し は、必要に応じて目的関数に追加のパラメータを渡す方法について説明します。

例

x = particleswarm(fun,nvars,lb,ub) は設計変数 x の下限と上限のセットを定義し、解が lb ≤ x ≤ ub の範囲で見つかるようにします。

例

x = particleswarm(fun,nvars,lb,ub,options) は、デフォルトの最適化パラメータを options の値に置き換えて最小化します。範囲が存在しない場合には lb = [] および ub = [] と設定してください。

x = particleswarm(problem) は、problem で説明されている構造体 problem の最小値を求めます。

例

[x,fval,exitflag,output,points] = particleswarm(___) は、前の構文のいずれかの入力引数の組み合わせを使用して、次の結果も返します。

  • fval、目的関数値fun(x)であるスカラー

  • exitflag、終了条件を表す値

  • output、最適化プロセスに関する情報を含む構造体

  • points は、points.X の最終的な群れの位置と、points.Fval の関連する目的関数の値を含む構造体です。

例

すべて折りたたむ

スクリプトを開く

2 つの変数の単純な関数を最小化します。

目的関数を定義します。

fun = @(x)x(1)*exp(-norm(x)^2);

関数を最小化するには particleswarm を呼び出します。

rng default  % For reproducibility
nvars = 2;
x = particleswarm(fun,nvars)

Optimization ended: relative change in the objective value 
over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.

x =

  629.4474  311.4814

関数プロットでわかるように、この解は真の最小値からは程遠いものです。

fsurf(@(x,y)x.*exp(-(x.^2+y.^2)))

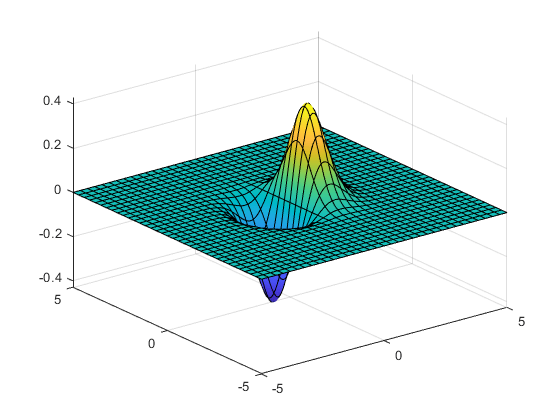
通常は、境界を設定するのが最善です。境界を持つ単純な関数を最小化するを参照してください。

ライブ スクリプトを開く

境界制約を持つ 2 つの変数の単純な関数を最小化します。

目的関数を定義します。 

fun = @(x)x(1)*exp(-norm(x)^2);

変数に境界を設定します。 

lb = [-10,-15];
ub = [15,20];

関数を最小化するには particleswarm を呼び出します。

rng default  % For reproducibility
nvars = 2;
x = particleswarm(fun,nvars,lb,ub)
Optimization ended: relative change in the objective value 
over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.

x = 1×2

   -0.7071   -0.0000
ライブ スクリプトを開く

より大きな集団とハイブリッド関数を使用して、より良い解決策を見つけてください。

目的関数と境界を指定します。 

fun = @(x)x(1)*exp(-norm(x)^2);
lb = [-10,-15];
ub = [15,20];

オプションを指定します。 

options = optimoptions('particleswarm','SwarmSize',100,'HybridFcn',@fmincon);

関数を最小化するには particleswarm を呼び出します。 

rng default  % For reproducibility
nvars = 2;
x = particleswarm(fun,nvars,lb,ub,options)
Optimization ended: relative change in the objective value 
over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.

x = 1×2

   -0.7071   -0.0000
ライブ スクリプトを開く

オプションの出力引数を返して、ソリューション プロセスをより詳細に調べます。

問題を定義します。 

fun = @(x)x(1)*exp(-norm(x)^2);
lb = [-10,-15];
ub = [15,20];
options = optimoptions('particleswarm','SwarmSize',50,'HybridFcn',@fmincon);

すべての出力で particleswarm を呼び出して関数を最小化し、解決プロセスに関する情報を取得します。 

rng default  % For reproducibility
nvars = 2;
[x,fval,exitflag,output,points] = particleswarm(fun,nvars,lb,ub,options)
Optimization ended: relative change in the objective value 
over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.

x = 1×2

   -0.7071   -0.0000


fval = -0.4289

exitflag = 1

output = struct with fields:
      rngstate: [1x1 struct]
    iterations: 43
     funccount: 2203
       message: 'Optimization ended: relative change in the objective value ...'
    hybridflag: 1


points = struct with fields:
       X: [50x2 double]
    Fval: [50x1 double]

入力引数

すべて折りたたむ

関数ハンドルまたは関数名として指定される目的関数。長さ nvars の行ベクトルを受け入れ、スカラー値を返す目的関数を記述します。

'UseVectorized' オプションが true の場合、pop 行 nvars 列の行列を受け入れるには fun と記述します。ここで、pop は現在の人口サイズです。この場合、fun は、フィットネス関数の値を含む pop と同じ長さのベクトルを返します。particleswarm はベクトル化された計算でも集団の単一のメンバーを渡すことができるため、fun が pop に対して特定のサイズを想定していないことを確認してください。

例: fun = @(x)(x-[4,2]).^2

データ型: char | function_handle | string

変数の数。正の整数として指定されます。ソルバーは長さ nvars から fun の行ベクトルを渡します。

例: 4

データ型: double

下限。実数ベクトルまたは倍精度浮動小数点配列として指定します。lb は、 lb ≤ x ≤ ub 内の要素ごとの下限を表します。

particleswarm は配列 lb をベクトル lb(:) に内部的に変換します。

例: lb = [0;-Inf;4] は x(1) ≥ 0, x(3) ≥ 4 を意味します。

データ型: double

上限は、実数ベクトルまたは倍精度浮動小数点数の配列として指定されます。ub は、 lb ≤ x ≤ ub 内の要素ごとの上限を表します。

particleswarm は配列 ub をベクトル ub(:) に内部的に変換します。

例: ub = [Inf;4;10] は x(2) ≤ 4, x(3) ≤ 10 を意味します。

データ型: double

optimoptions 関数の出力として指定される particleswarm のオプション。

一部のオプションは、optimoptions に表示されません。これらのオプションは斜体で表示されます。詳細については、最適化オプションの表示 を参照してください。

CreationFcn

初期の群れを作成する関数。'pswcreationuniform' または関数ハンドルとして指定します。既定値は 'pswcreationuniform' です。スウォームの作成を参照してください。

Display

コマンド ラインに返される表示のレベル。

  • 'off' または 'none' — 出力を表示しない。

  • 'final' (既定の設定) — 最終出力のみを表示する。

  • 'iter' — 各反復の出力を表示する。

DisplayInterval反復表示の間隔。反復表示では、DisplayInterval 回の反復ごとに 1 行が出力されます。既定値は 1 です。
FunctionToleranceデフォルトが 1e-6 の非負のスカラー。最後の MaxStallIterations 回の反復における最良目的関数値の相対的な変化が options.FunctionTolerance 未満になると、反復は終了します。
FunValCheck

目的関数と制約の値が有効かどうかを確認します。目的関数または制約が複素数、Inf、または NaN の値を返す場合、'on' はエラーを表示します。既定の 'off' ではエラーを表示しません。

HybridFcn

particleswarm が終了した後も最適化を継続する関数。名前または関数ハンドルとして指定します。取りうる値は以下のとおりです。

  • 'fmincon'

  • 'fminsearch'

  • 'fminunc'

  • 'patternsearch'

{@fmincon,fminconopts} など、ハイブリッド関数とそのオプションを指定するセル配列にすることもできます。既定値は [] です。ハイブリッド機能を参照してください。

ハイブリッド関数を使用する場合を参照してください。

InertiaRange昇順で同じ符号値を持つ 2 要素の実数ベクトル。適応慣性の下限と上限を指定します。一定の（非適応）慣性を得るには、InertiaRange の両方の要素を同じ値に設定します。既定値は [0.1,1.1] です。粒子群最適化アルゴリズムを参照してください。
InitialPoints

マトリックスまたは構造として指定された、粒子の初期集団または部分集団。

  • 行列のサイズは M 行 nvars 列です。各行は 1 つの粒子を表します。M < SwarmSize の場合、 particleswarm はさらに多くの粒子を生成するので、合計数は SwarmSize になります。M > SwarmSize の場合、particleswarm は最初の SwarmSize 行を使用します。

  • 構造体には、初期点の行列を表すフィールド X が必要です。

  • 構造に複数のフィールドがある場合、その構造には、ポイント InitialPoints.X の目的関数値のベクトルを含むフィールド Fval が含まれている必要があります。

InitialSwarmSpan

@pswcreationuniform が作成するパーティクル位置の初期範囲。正のスカラーまたは nvars 要素を持つベクトルになります。ここで、nvars は変数の数です。パーティクル コンポーネントの範囲は -InitialSwarmSpan/2,InitialSwarmSpan/2 であり、境界に一致するように必要に応じてシフトおよびスケーリングされます。既定値は 2000 です。

InitialSwarmSpan は初期粒子速度の範囲にも影響します。初期化を参照してください。

MaxIterationsparticleswarm が実行する反復の最大回数。デフォルトは 200*nvars です。ここで nvars は変数の数です。
MaxStallIterationsデフォルトは 20 の正の整数。最後の MaxStallIterations 回の反復における最良目的関数値の相対的な変化が options.FunctionTolerance 未満になると、反復は終了します。
MaxStallTime既知の最良の目的関数値が改善されない最大秒数。デフォルトは Inf の正のスカラー。
MaxTimeparticleswarm が実行される最大時間 (秒)。既定値は Inf です。
MinNeighborsFraction最小適応近傍サイズ、0 から 1 までのスカラー。既定値は 0.25 です。粒子群最適化アルゴリズムを参照してください。
ObjectiveLimit最小目標値、停止基準。スカラー、デフォルトは -Inf です。
OutputFcn関数ハンドルまたは関数ハンドルのセル配列。出力関数は反復データを読み取り、ソルバーを停止できます。既定値は [] です。出力関数とプロット関数を参照してください。
PlotFcn関数名、関数ハンドル、または関数ハンドルのセル配列。カスタム プロット関数の場合は、関数ハンドルを渡します。プロット関数は反復データを読み取り、各反復をプロットし、ソルバーを停止できます。既定値は [] です。利用可能な組み込みプロット関数: 'pswplotbestf' 。出力関数とプロット関数を参照してください。
SelfAdjustmentWeight速度を調整するときに各パーティクルの最適な位置に重み付けします。デフォルトが 1.49 の有限スカラー。粒子群最適化アルゴリズムを参照してください。
SocialAdjustmentWeight速度を調整するときに近傍の最適な位置に重み付けします。デフォルトが 1.49 の有限スカラー。粒子群最適化アルゴリズムを参照してください。
SwarmSize群れの中の粒子の数。1 より大きい整数。デフォルトは min(100,10*nvars) です。ここで nvars は変数の数です。
UseParalleltrue の場合に目的関数を並列に計算します。既定値は false です。並列またはベクトル化された関数評価を参照してください。
UseVectorizedtrue の場合にベクトル化された形式で目的関数を計算します。既定値は false です。並列またはベクトル化された関数評価を参照してください。

最適化問題は、次のフィールドを含む構造体として指定されます。

solver'particleswarm'
objective目的関数への関数ハンドル、または目的関数の名前。
nvars問題内の変数の数。
lb下限のベクトルまたは配列。
ub上限のベクトルまたは配列。
optionsoptimoptions によって作成されたオプション。
rngstate解決プロセスの開始時の乱数ジェネレーターのオプションの状態。

データ型: struct

出力引数

すべて折りたたむ

ソリューションは、任意の境界制約に従って目的関数を最小化する実数ベクトルとして返されます。

目的の値。実数スカラー fun(x) として返されます。

アルゴリズムの停止条件。アルゴリズムの停止理由を識別する整数として返されます。exitflag の値と particleswarm が停止した対応する理由を以下に示します。

1

前回の options.FunctionTolerance 回の反復で目的値の相対変化が options.MaxStallIterations より小さくなっていることを示します。

0

反復数が options.MaxIterations を超過しています。

-1

出力関数またはプロット関数によって反復が停止したことを示します。

-2

範囲に整合性がないことを示します。つまり、一部の i について、lb(i) > ub(i) です。

-3

最良の目的関数値が options.ObjectiveLimit を下回っていることを示します。

-4

最良の目的関数値が options.MaxStallTime 秒以内に変化しなかったことを示します。

-5

実行時間が options.MaxTime 秒を超えたことを示します。

最適化プロセスに関する情報を含む構造体として返された解法プロセスの概要。

iterations

ソルバーの反復回数

funccount

目的関数の評価回数。

message

アルゴリズムが停止した理由。

hybridflag

ハイブリッド関数からの終了フラグ。HybridFcn options に関連します。

rngstate

アルゴリズムが開始する直前のデフォルトの乱数ジェネレーターの状態。

最終的な群れの位置と目的関数の値は、次のフィールドを持つ構造体として返されます。

  • X — 最終的な群れの位置が行列として返されます。行列の各行は 1 つの点を表します。

  • Fval — 最終的な群れの目的関数の値。各 i について、最終的な群れ points.Fval(i) = fun(points.X(i)) のメンバーのインデックス。

最適化を続行するには、points を InitialPoints オプションとして渡すことができます。ただし、このアプローチは、最適化を最終集団から再開するときにアルゴリズムの多くの側面が同一ではないため、最初からより長い時間にわたって最適化を実行することと同じではありません。粒子群最適化アルゴリズムを参照してください。

データ型: struct

制限

  • 問題ベースの 最適化 ライブ エディター タスクでは、現在、複数の初期ポイントまたは初期目的関数値の指定はサポートされていません。初期ポイントを指定するには、ソルバーベースのタスクを使用するか、コマンド ラインを使用します。

アルゴリズム

粒子群最適化アルゴリズムの説明については、粒子群最適化アルゴリズム を参照してください。

代替機能

アプリ

[最適化] ライブ エディター タスクが particleswarm にビジュアル インターフェイスを提供します。

拡張機能

バージョン履歴

R2014b で導入

すべて展開する

参考

| |

トピック