自動微分の背景

自動微分とは

自動微分 ("autodiff"、"AD"、または "アルゴリズム微分" とも呼ばれる) は、最適化で広く使用されるツールです。solve 関数は、一般的な非線形目的関数と制約の問題ベースの最適化で既定で自動微分を使用します。Optimization Toolbox の自動微分を参照してください。

自動微分は、導関数 (勾配) を数値的に評価する手法のセットです。この方法では、有限差分近似より正確な微分のシンボリック規則を使用します。純粋にシンボリックな方法とは異なり、自動微分は大規模なシンボリック計算を行うのではなく、計算の初期に式を数値的に評価します。つまり、自動微分は、特定の数値で導関数を評価します。導関数の記号式を作成することはありません。

"フォワードモード" の自動微分は、基本的な導関数演算と関数自体を評価する演算を同時に実行することによって、数値導関数を評価します。次のセクションで詳しく説明しますが、ソフトウェアは、これらの計算を計算グラフ上で実行します。
"リバースモード" の自動微分では、フォワードモードの計算グラフの拡張機能を使用して、グラフのリバース走査による勾配の計算を可能にします。ソフトウェアはコードを実行して関数とその導関数を計算すると、演算を "トレース" と呼ばれるデータ構造に記録します。

多くの研究者 (Baydin、Pearlmutter、Radul、および Siskind [1] など) が言及しているように、多くの変数のスカラー関数では、リバースモードのほうがフォワードモードより効率的に勾配を計算します。目的関数はスカラーのため、solve 自動微分はスカラー最適化にリバースモードを使用します。ただし、非線形最少二乗のようなベクトル値関数や方程式求解の場合、solve は計算にフォワードモードを使用する場合があります。Optimization Toolbox の自動微分を参照してください。

フォワードモード

次の関数とその勾配を評価する問題を考えます。

$f (x) = x_{1} \exp (- \frac{1}{2} (x_{1}^{2} + x_{2}^{2})) .$

自動微分は特別な点で機能します。この場合、x₁ = 2、x₂ = 1/2 とします。

次の計算グラフは、関数 f(x) の計算を符号化します。

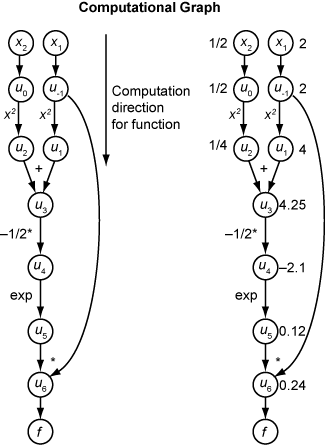
フォワードモードを使用して f(x) の勾配を計算するには、同じグラフを同じ方向で計算します。ただし、微分の基本的な規則に基づいて計算に変更を加えます。計算をさらに簡略化するには、処理を進めながら各部分式 u_i の微分の値を埋めます。勾配全体を計算するには、各独立変数に関する偏微分に対して 1 回ずつ、グラフを 2 回走査しなければなりません。連鎖律の各部分式に数値があるため、式全体の評価グラフが関数自体と同じ種類になります。

計算では連鎖律が繰り返し適用されます。この例では、x₁ に関する f の導関数が次の式に展開されます。

$\begin{matrix} \frac{d f}{d x_{1}} = \frac{d u_{6}}{d x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial u_{3}} \frac{\partial u_{3}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial u_{3}} \frac{\partial u_{3}}{\partial u_{1}} \frac{\partial u_{1}}{\partial x_{1}} . \end{matrix}$

${\dot{u}}_{i}$ で x₁ に関する式 u_i の導関数を表してみましょう。下の図に示すように、関数評価からの u_i の評価値を使用して、x₁ に関する f の偏導関数を計算します。 ${\dot{u}}_{i}$ のすべての値が、グラフを上から下に移動するときに入手できることに注意してください。

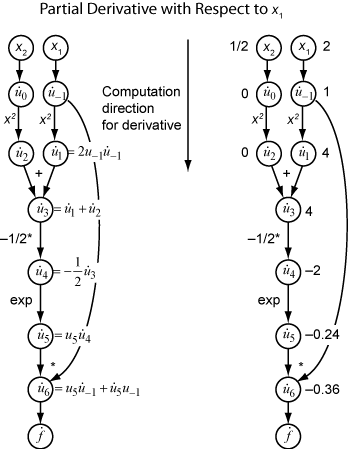
x₂ に関する偏導関数を計算するには、同様の計算グラフを移動します。そのため、関数の勾配を計算すると、グラフトラバーサルの回数が変数の数と同じになります。目的関数または非線形制約が多くの変数に依存している場合は、多くの用途でこのプロセスの実行速度が遅くなる可能性があります。

リバースモード

リバースモードでは、計算グラフのフォワード走査を 1 回使用してトレースを設定します。その後で、グラフの 1 回のリバーストラバーサルで関数の勾配全体を計算します。多くの変数を含む問題では、このモードがはるかに効率的です。

リバースモードの背後にある理論も、上線で示される関連する随伴変数とともに、連鎖律に基づきます。u_i の随伴変数は次のとおりです。

${\bar{u}}_{i} = \frac{\partial f}{\partial u_{i}} .$

計算グラフの観点では、1 つの変数から伸びる矢印が、連鎖律の項別に対応する随伴変数に寄与します。たとえば、変数 u_–1 からは 2 つの変数 u₁ および u₆ に向かって矢印が出ています。グラフには、次の方程式が関連付けられています。

$\begin{matrix} \frac{\partial f}{\partial u_{- 1}} = \frac{\partial f}{\partial u_{1}} \frac{\partial u_{1}}{\partial u_{- 1}} + \frac{\partial f}{\partial u_{6}} \frac{\partial u_{6}}{\partial u_{- 1}} \\ = {\bar{u}}_{1} \frac{\partial u_{1}}{\partial u_{- 1}} + {\bar{u}}_{6} \frac{\partial u_{6}}{\partial u_{- 1}} . \end{matrix}$

この計算では、 $u_{1} = u_{- 1}^{2}$ と u₆ = u₅u_–1 を思い出すことによって、次の式が得られます。

${\bar{u}}_{- 1} = {\bar{u}}_{1} 2 u_{- 1} + {\bar{u}}_{6} u_{5} .$

グラフのフォワードトラバーサル中は、ソフトウェアが中間変数 u_i を計算します。シード値 ${\bar{u}}_{6} = \frac{\partial f}{\partial f} = 1$ で始まるリバーストラバーサル中は、リバースモード計算によって、すべての変数の随伴行列値が得られます。そのため、リバースモードでは、1 回の計算だけで勾配が計算されるため、フォワードモードに比べて大幅な時間の節約になります。

下の図は、関数のリバースモードでの勾配の計算を示しています。

$f (x) = x_{1} \exp (- \frac{1}{2} (x_{1}^{2} + x_{2}^{2})) .$

繰り返しになりますが、この計算では x₁ = 2 と x₂ = 1/2 を使用します。リバースモードの計算は、元の計算グラフでの関数の計算時に取得された u_i の値に依存します。図の右側の部分では、図の左側の部分からの公式を使用して計算された随伴変数の値が、随伴変数名の横に表示されています。

最終勾配値が ${\bar{u}}_{0} = \frac{\partial f}{\partial u_{0}} = \frac{\partial f}{\partial x_{2}}$ および ${\bar{u}}_{- 1} = \frac{\partial f}{\partial u_{- 1}} = \frac{\partial f}{\partial x_{1}}$ として表示されています。

詳細については、Baydin、Pearlmutter、Radul、および Siskind [1] または自動微分に関する Wikipedia の記事[2]を参照してください。

閉形式

線形または二次の目的関数または制約関数では、係数から非常に低い計算コストで勾配を明示的に使用できます。このような場合、solve と prob2struct は AD を使用せずに勾配を明示的に提供し、適用可能なソルバーは常に勾配を使用します。output 構造体を取得すると、関連する objectivederivative フィールドまたは constraintderivative フィールドの値は "closed-form" になります。

Optimization Toolbox の自動微分

自動微分 (AD) は、以下の条件の下で、solve 関数と prob2struct 関数に適用されます。

最適化変数および式でサポートされる演算で説明されているように、目的関数と制約関数がサポートされています。これらの関数は、fcn2optimexpr 関数を使用する必要がありません。
solve に呼び出されるソルバーは、fmincon、fminunc、fsolve、lsqnonlin のいずれかです。
最適化問題では、solve または prob2struct の 'ObjectiveDerivative' と 'ConstraintDerivative' の名前と値のペアの引数が 'auto' (既定)、'auto-forward'、または 'auto-reverse' に設定されます。
方程式問題の場合、'EquationDerivative' オプションは 'auto' (既定)、'auto-forward'、または 'auto-reverse' に設定されます。

AD の適用時	サポートされているすべての制約関数	サポートされていない 1 つ以上の制約
サポートされている目的関数	目的と制約に使用される AD	目的のみに使用される AD
サポートされていない目的関数	制約のみに使用される AD	使用されない AD

メモ

線形または二次の目的関数または制約関数では、適用可能なソルバーは常に関数の明示的な勾配を使用します。このような勾配は AD を使用して生成されません。閉形式を参照してください。

これらの条件が満たされなかった場合は、solve が有限差分によって勾配を推定し、prob2struct が生成された関数ファイル内に勾配を作成しません。

ソルバーは既定で次のタイプの AD を選択します。

一般的な非線形目的関数の場合、fmincon は既定で目的関数用のリバースモードの AD になります。fmincon は、非線形制約の数が変数の数よりも少ない場合に既定で非線形制約関数用のリバースモードの AD になります。それ以外の場合、fmincon は既定で非線形制約関数用のフォワードモードの AD になります。
一般的な非線形目的関数の場合、fminunc は既定でリバースモードの AD になります。
最小二乗目的関数の場合、fmincon と fminunc は既定で目的関数用のフォワードモードの AD になります。問題ベースの最小二乗目的関数の定義については、問題ベースの最小二乗法の目的関数の記述を参照してください。
lsqnonlin は、目的ベクトルに含まれる要素数が変数の数以上である場合に既定でフォワードモードの AD になります。それ以外の場合、lsqnonlin は既定でリバースモードの AD になります。
fsolve は、方程式の数が変数の数以上の場合に既定でフォワードモードの AD になります。それ以外の場合、fsolve は既定でリバースモードの AD になります。

メモ

prob2struct によって変換された問題内で自動導関数を使用するには、これらの導関数を指定するオプションを渡します。

options = optimoptions('fmincon','SpecifyObjectiveGradient',true,...
    'SpecifyConstraintGradient',true);
problem.options = options;

現時点で、AD は、1 階微分に対してのみ機能します。2 階以上の微分には適用されません。そのため、たとえば、解析的ヘッシアンを使用して最適化を高速化するには、solve を直接使用できず、代わりに、問題ベースのワークフローへの導関数の供給で説明されているアプローチを使用しなければなりません。

参照

[1] Baydin, Atilim Gunes, Barak A. Pearlmutter, Alexey Andreyevich Radul, and Jeffrey Mark Siskind. "Automatic Differentiation in Machine Learning: A Survey." The Journal of Machine Learning Research, 18(153), 2018, pp. 1–43. Available at https://arxiv.org/abs/1502.05767.

[2] Automatic differentiation. Wikipedia. Available at https://en.wikipedia.org/wiki/Automatic_differentiation.

参考

solve | prob2struct