fminbnd
固定区間における 1 変数関数の局所的最小値を求める
構文
説明
fminbnd は、以下で指定される問題の局所的最小値を求める 1 次元最小化関数です。
x、x1、x2 は有限スカラーであり、f(x) はスカラーを返す関数です。
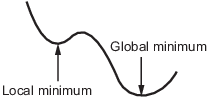
区間 (x1,x2) に複数の局所的最小値が存在する場合、fminbnd は 1 つだけを返しますが、これが大域的最小値であることは保証されません。詳細については、局所的最小値と大域的最小値を参照してください。
例
入力引数
出力引数
制限
最小化する関数は、連続でなければなりません。
fminbndは局所解のみを返す場合があります。関数
fminbndは、解が区間の境界上にあるときに遅い収束を示すことがあります。
詳細
アルゴリズム
fminbnd は関数ファイルです。そのアルゴリズムは黄金分割探索と放物線内挿に基づいています。左の端点 x1 が右の端点 x2 と極めて近接している場合を除き、fminbnd はこれらの端点で fun を評価しません。したがって、区間 x1 < x < x2 における x に対して fun を定義するだけですみます。
最小値が実際に x1 または x2 で発生する場合、fminbnd は区間 (x1,x2) の内側にあり最小点に近い点 x を返します。この場合、最小点から x までの距離は 2*(TolX + 3*abs(x)*sqrt(eps)) 以下です。アルゴリズムの詳細については、[1]または[2]を参照してください。
代替機能
アプリ
[最適化] ライブ エディター タスクは、fminbnd のビジュアル インターフェイスを提供します。
参照
[1] Forsythe, G. E., M. A. Malcolm, and C. B. Moler. Computer Methods for Mathematical Computations. Englewood Cliffs, NJ: Prentice Hall, 1976.
[2] Brent, Richard. P. Algorithms for Minimization without Derivatives. Englewood Cliffs, NJ: Prentice-Hall, 1973.
拡張機能
バージョン履歴
R2006a より前に導入