Main Content

このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

信号モデリング

線形予測、自己回帰 (AR) モデル、ユール・ウォーカー、レビンソン・ダービン

Signal Processing Toolbox™ には、信号、システムまたはプロセスを記述する有理伝達関数を推定できるパラメトリック モデリング手法が用意されています。信号に関する既知の情報を使用し、信号をモデル化する線形システムの係数を求めます。Prony 法およびスティグリッツ・マクブライド法の ARX モデルを使用して、与えられた時間領域インパルス応答を近似します。与えられた複素周波数応答に一致するアナログまたはデジタル伝達関数を求めます。線形予測フィルターを使用して共振をモデル化します。

関数

すべて展開する

corrmtx自己相関行列の推定に使用するデータ行列
levinsonレビンソン・ダービン再帰法
lpc線形予測フィルター係数
rlevinson逆レビンソン・ダービン再帰法
schurrc自己相関列からの反射係数の計算
xcorr相互相関
xcov相互共分散
ac2poly自己相関列の予測多項式への変換
ac2rc自己相関列を反射係数に変換
is2rc逆正弦パラメーターを反射係数に変換
lar2rc対数面積比を表すパラメーターを反射係数に変換
lsf2poly線スペクトル周波数を予測フィルター係数に変換
poly2ac予測フィルター多項式の自己相関列への変換
poly2lsf予測フィルター係数の線スペクトル周波数への変換
poly2rc予測フィルター多項式の反射係数への変換
rc2ac反射係数の自己相関列への変換
rc2is反射係数の逆正弦パラメーターへの変換
rc2lar反射係数の対数面積比パラメーターへの変換
rc2poly反射係数の予測フィルター多項式への変換
arburg自己回帰全極モデルパラメーター — バーグ法
arcov自己回帰全極モデル パラメーター — 共分散法
armcov自己回帰全極モデル パラメーター — 修正共分散法
aryule自己回帰全極モデル パラメーター — ユール・ウォーカー法
invfreqs周波数応答データからの連続時間フィルター パラメーターの同定
invfreqz周波数応答データからの離散時間フィルター パラメーターの同定
pronyProny 法によるフィルター設計
stmcbスティグリッツ・マクブライド反復法を使用した線形モデルの計算

トピック

  • 線形予測と自己回帰モデリング

    線形フィルターのパラメーターを確定するため、2 つの方法 (自己回帰モデリングと線形予測) を比較します。

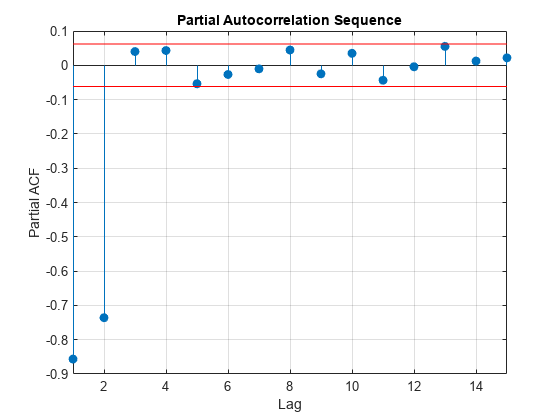
  • 偏自己相関列による AR 次数選択

    偏自己相関列を使用して自己回帰モデルの次数を評価します。

  • パラメトリック モデリング

    信号、システム、または変動過程を記述する数学モデルに関するパラメーターを求める手法を学習します。

  • 予測多項式

    自己相関列から予測多項式を求めます。結果として得られる予測多項式が安定な全極フィルターを生成する逆数をもつことを確認します。