このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

偏自己相関列による AR 次数選択

この例は、偏自己相関列を使用して自己回帰モデルの次数を評価する方法を示しています。値 $$X(1),X(2),X(3),\dots ,X(k+1)$$ をもつ定常な時系列において、ラグ $$k$$ における偏自己相関列は、介在観測値 $$X(2),X(3),X(4),\dots ,X(k)$$ における $$X(1)$$ および $$X(k+1)$$ の回帰推定後の、$$X(1)$$ と $$X(k+1)$$ との相関です。移動平均過程では、自己相関列を使用して次数を評価することができます。しかし、自己回帰 (AR) 過程または自己回帰移動平均 (ARMA) 過程では、自己相関列は次数選択の役には立ちません。この例では、AR 過程におけるモデル次数の選択に次のワークフローを使用します。

• AR(2) 過程の実現をシミュレート

• 時系列の遅延した値同士の相関をグラフにより考察

• 時系列サンプルの自己相関列の調査

• ユール・ウォーカー式を解くことによる時系列の AR(15) モデル近似 (aryule)

• aryule によって返される反射係数を使用した偏自己相関列の計算

• モデル次数選択のための偏自己相関列の調査

以下で定義される AR(2) 過程を考えます。

$$X(n)+1.5X(n-1)+0.75X(n-2)=\epsilon (n),$$

ここで、$$\epsilon (n)$$ は $$N(0,1)$$ ガウス ホワイト ノイズ過程です。差分方程式により定義された AR(2) 過程からの 1000 サンプルの時系列をシミュレートします。再現性のある結果を得るために、乱数発生器を既定の状態に設定します。

A = [1 1.5 0.75];
rng default
x = filter(1,A,randn(1000,1));

AR(2) 過程の周波数応答を表示します。

freqz(1,A)

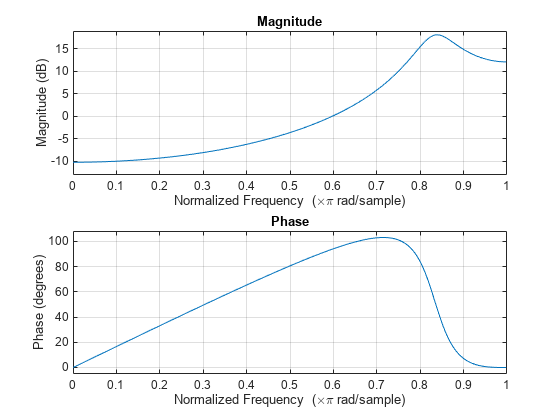
この場合、AR(2) 過程はハイパス フィルターのように機能します。

$$n=2,3,4,5$$ について $$X(n+1)$$ 対 $$X(1)$$ の散布図を作成することによって、x における相関をグラフを使用して調査します。

figure
for k = 1:4
    subplot(2,2,k)
    plot(x(1:end-k),x(k+1:end),'*')
    xlabel('X_1')
    ylabel(['X_' int2str(k+1)])
    grid
end

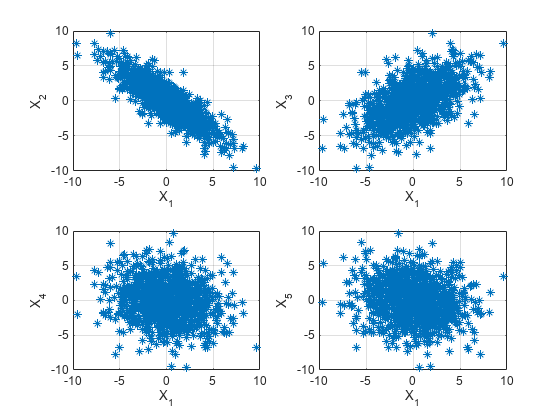
散布図では、$$X(1)$$ と $$X(2)$$ 間、$$X(1)$$ と $$X(3)$$ に線形関係があります。しかし、$$X(1)$$ と $$X(4)$$ または $$X(5)$$ との間にはいずれも線形関係はありません。

上段の散布図において、点はおおよそ直線に並び、左上のパネルでは負の勾配を、右上のパネルでは正の勾配をもっています。下の 2 つのパネルでは、散布図は明らかな線形関係を示してはいません。

$$X(1)$$ と $$X(2)$$ 間の負の相関関係および $$X(1)$$ と $$X(3)$$ 間の正の相関関係は、AR(2) 過程のハイパス フィルター動作に起因します。

サンプルの自己相関列をラグ 50 まで求めて結果をプロットします。

[xc,lags] = xcorr(x,50,'coeff');

figure
stem(lags(51:end),xc(51:end),'filled')
xlabel('Lag')
ylabel('ACF')
title('Sample Autocorrelation Sequence')
grid

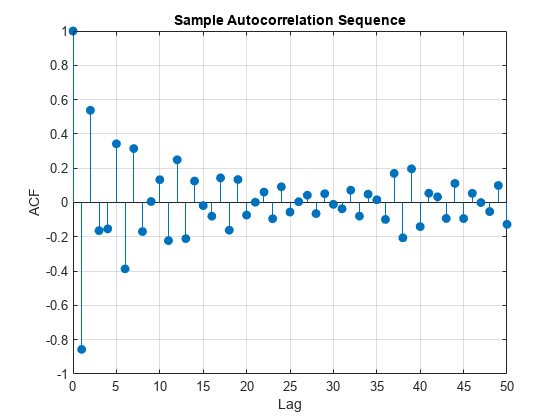
サンプルの自己相関列は、ラグ 1 で負の値、ラグ 2 で正の値を示しています。散布図に基づけば、これは予想どおりの結果です。ただし、サンプルの自己相関列から AR モデルの適切な次数を決定することはできません。

aryule を使用して AR(15) モデルを近似します。負が偏自己相関列である反射係数のシーケンスを返します。

[arcoefs,E,K] = aryule(x,15);
pacf = -K;

大きいサンプルの 95% 信頼区間で偏自己相関列をプロットします。次数 $$p$$ の自己回帰過程によってデータが生成される場合、サンプルの偏自己相関列の $$p$$ より大きいラグにおける値は、$$N(0,1/N)$$ 分布に従います。ここで、$$N$$ は時系列の長さです。95% 信頼区間に対する棄却限界値は $$\sqrt{2}{erf}^{-1}(0.95)\approx 1.96$$ で、信頼区間は $$\Delta =0\pm 1.96/\sqrt{N}$$ となります。

stem(pacf,'filled')
xlabel('Lag')
ylabel('Partial ACF')
title('Partial Autocorrelation Sequence')
xlim([1 15])

conf = sqrt(2)*erfinv(0.95)/sqrt(1000);
hold on
plot(xlim,[1 1]'*[-conf conf],'r')
hold off
grid

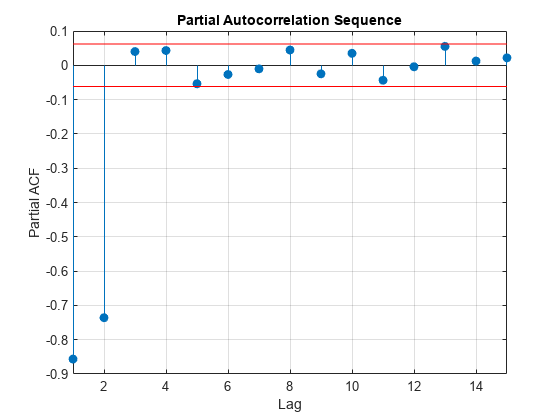
偏自己相関列の値が 95% 信頼限界の外側にあるのは、ラグ 1 およびラグ 2 だけです。このことは AR 過程の正しいモデル次数が 2 であることを示しています。

この例では、AR(2) 過程をシミュレートするために時系列を生成しました。偏自己相関列はその結果の確認にとどまっています。実際には、モデル次数についての事前情報の無い、観察されただけの時系列を扱います。実際的なケースでは、偏自己相関列は、定常な自己回帰時系列において適切なモデル次数を選択するための重要なツールです。

参考

aryule | xcorr

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい