予測多項式

この例は、自己相関列から予測多項式を求める方法を示しています。この例では、結果として得られる予測多項式が安定な全極フィルターを生成する逆数をもつことも示します。全極フィルターを使用して広義定常性ホワイト ノイズ列をフィルター処理して、広義定常性自己回帰過程を生成することができます。

以下によって定義された自己相関列を作成します。

$$r(k)=\frac{24}{5}{2}^{-\left|k\right|}-\frac{27}{10}{3}^{-\left|k\right|},k=0,1,2.$$

k = 0:2;
rk = (24/5)*2.^(-k)-(27/10)*3.^(-k);

次のように ac2poly を使用して次数 2 の予測多項式を求めます。

$$A(z)=1-\frac{5}{6}{z}^{-1}+\frac{1}{6}{z}^{-2}.$$

A = ac2poly(rk);

FIR フィルターの極-零点プロットを調べて、零点が単位円の中にあることを確かめます。

zplane(A,1)
grid

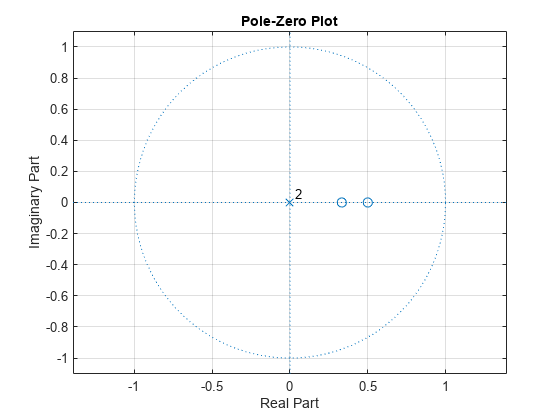
逆全極フィルターは極が単位円内にあるとき安定です。

zplane(1,A)
grid
title('Poles and Zeros')

全極フィルターを使用して、ホワイト ノイズ列から広義定常性 AR(2) 過程の実現を生成します。再現性のある結果を得るために、乱数発生器を既定の状態に設定します。

rng default

x = randn(1000,1);
y = filter(1,A,x);

AR(2) 実現のサンプルの自己相関列を計算して、サンプルの自己相関列が真の自己相関列に近いことを示します。

[xc,lags] = xcorr(y,2,'biased');
[xc(3:end) rk']

ans = 3×2

    2.2401    2.1000
    1.6419    1.5000
    0.9980    0.9000