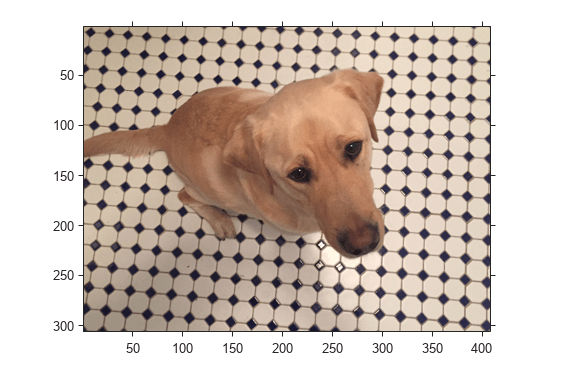
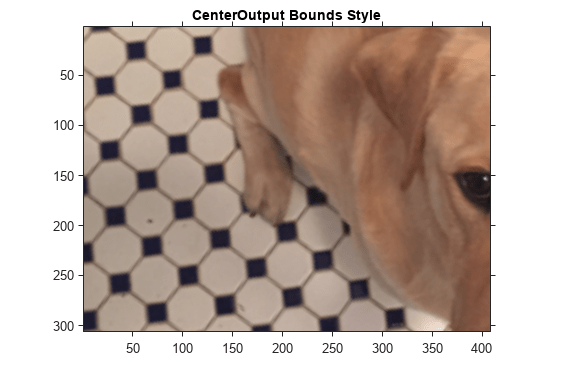
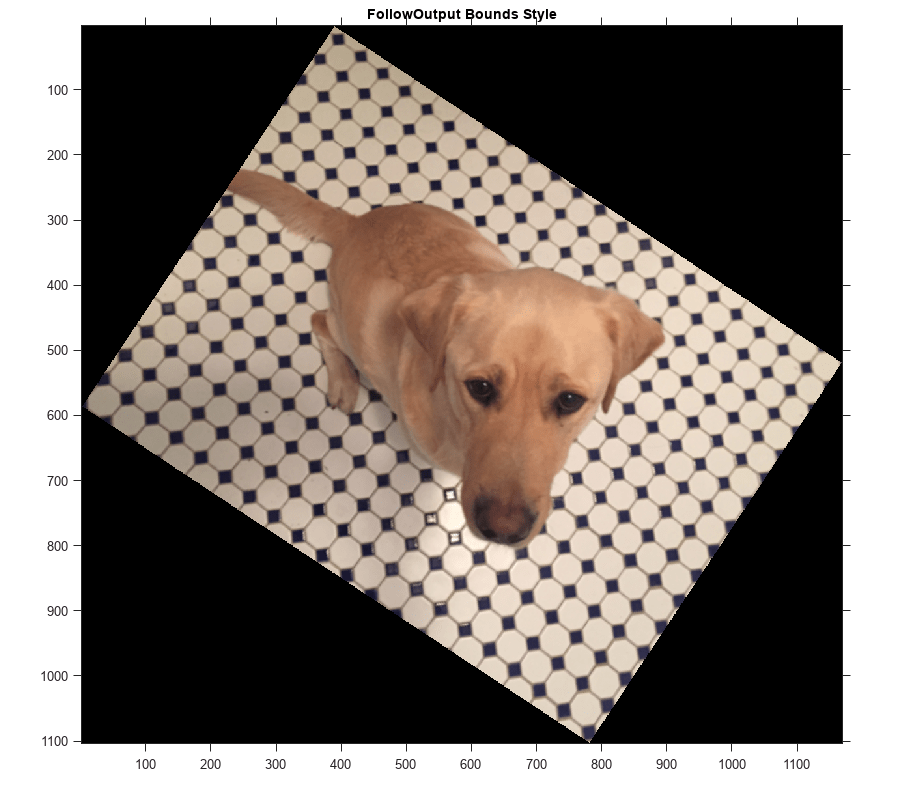
imwarp

イメージへの幾何学的変換の適用

構文

B = imwarp(A,tform)

B = imwarp(A,D)

[B,RB] = imwarp(A,RA,tform)

[___] = imwarp(___,interp)

[___] = imwarp(___,Name=Value)

説明

B = imwarp(A,tform) は、幾何学的変換 tform に従って数値イメージ、論理イメージ、または categorical イメージ A を変換します。関数は変換されたイメージを B に返します。

B = imwarp(A,D) は、変位場 D に従ってイメージ A を変換します。

[B,RB] = imwarp(A,RA,tform) は、イメージ データ A およびこれに関連付けられた空間参照オブジェクト RA によって指定される空間参照イメージを変換します。出力は、イメージ データ B およびこれに関連付けられた空間参照オブジェクト RB によって指定される空間参照イメージです。

[___] = imwarp(___,interp) は、使用する内挿のタイプを指定します。

[___] = imwarp(___,Name=Value) は、幾何学的変換のさまざまな特性を制御する名前と値の引数を指定します。

ヒント

入力の変換 tform でフォワード変換を定義しない場合は、名前と値の引数 OutputView を使用して変換を高速化します。

例

イメージへの水平せん断の適用

グレースケール イメージを読み取り、それを表示します。

I = imread('cameraman.tif');
imshow(I)

2 次元アフィン変換を作成します。

A = [1 0.5 0; 0 1 0; 0 0 1];
tform = affinetform2d(A);

変換をイメージに適用します。

J = imwarp(I,tform);
imshow(J)

3 次元 MRI データへの回転変換の適用

3 次元 MRI ボリューム イメージを読み込んで表示します。

load("mri");
mriVolume = squeeze(D);
volshow(mriVolume);

y 軸に対してイメージを回転した 3 次元剛体変換オブジェクトを作成します。

theta = [0 22.5 0];
transl = [0 0 0];
tform = rigidtform3d(theta,transl);

変換をイメージに適用し、結果を表示します。

mriVolumeRotated = imwarp(mriVolume,tform);
volshow(mriVolumeRotated);

さまざまな出力表示スタイルを使用したイメージのワープ

イメージを読み取って表示します。イメージの空間範囲を確認するには、座標軸を表示します。

A = imread("kobi.png");
A = imresize(A,0.25);
iptsetpref("ImshowAxesVisible","on")
imshow(A)

2 次元アフィン変換を作成します。この例では、範囲 [1.2, 2.4] の係数でのスケーリング、範囲 [-45, 45] 度の角度での回転、範囲 [100, 200] ピクセルの距離での水平方向の平行移動で構成されるランダムな変換を作成します。

tform = randomAffine2d("Scale",[1.2,2.4],"XTranslation",[100 200],"Rotation",[-45,45]);

イメージと変換について 3 つの異なる出力表示を作成します。

centerOutput = affineOutputView(size(A),tform,"BoundsStyle","CenterOutput");
followOutput = affineOutputView(size(A),tform,"BoundsStyle","FollowOutput");
sameAsInput = affineOutputView(size(A),tform,"BoundsStyle","SameAsInput");

異なる出力表示スタイルをそれぞれ使用して、入力イメージに変換を適用します。

BCenterOutput = imwarp(A,tform,"OutputView",centerOutput);
BFollowOutput = imwarp(A,tform,"OutputView",followOutput);
BSameAsInput = imwarp(A,tform,"OutputView",sameAsInput);

結果のイメージを表示します。

imshow(BCenterOutput)
title("CenterOutput Bounds Style");

imshow(BFollowOutput)
title("FollowOutput Bounds Style");

imshow(BSameAsInput)
title("SameAsInput Bounds Style");

iptsetpref("ImshowAxesVisible","off")

入力引数

A — 変換されるイメージ

数値配列 | logical 配列 | categorical 配列

変換されるイメージ。任意の次元の数値配列、logical 配列、または categorical 配列として指定します。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | categorical

tform — 幾何学的変換

幾何学的変換オブジェクト

幾何学的変換。表に記載されている幾何学的変換オブジェクトとして指定します。

幾何学的変換オブジェクト	説明
2 次元線形幾何学的変換
transltform2d	平行移動変換
rigidtform2d	剛体変換: 平行移動と回転
simtform2d	相似変換: 平行移動、回転、等方性スケーリング
affinetform2d	アフィン変換: 平行移動、回転、異方性スケーリング、鏡映、せん断
projtform2d	射影変換
3 次元線形幾何学的変換
transltform3d	平行移動変換
rigidtform3d	剛体変換: 平行移動と回転
simtform3d	相似変換: 平行移動、回転、等方性スケーリング
affinetform3d	アフィン変換: 平行移動、回転、異方性スケーリング、鏡映、せん断
非線形幾何学的変換
geometricTransform2d	2 次元幾何学的変換
geometricTransform3d	3 次元幾何学的変換
PolynomialTransformation2D	多項式変換
PiecewiseLinearTransformation2D	区分的線形変換
LocalWeightedMeanTransformation2D	局所重み付き平均変換

• tform が 2 次元で、A が 2 次元より大きい場合 (たとえば、RGB イメージなど)、imwarp は、より高い次元に沿ったすべての 2 次元平面に同じ 2 次元変換を適用します。

• tform が 3 次元の場合、A は 3 次元イメージ ボリュームでなければなりません。

メモ

tform は、タイプ rigid2d、rigid3d、affine2d、affine3d、または projective2d のオブジェクトとして指定することもできます。ただし、これらのオブジェクトは推奨されません。詳細については、互換性の考慮事項を参照してください。

D — 変位場

数値配列

変位場。数値配列として指定します。変位場は出力イメージのグリッド サイズと位置を定義します。変位値の単位はピクセルです。imwarp では、D は既定の固有座標系を基準とすると仮定しています。変位場の推定には、imregdemons を使用します。

• A が m 行 n 列の 2 次元グレースケール イメージの場合、m x n x 2 の配列として変位場を指定します。D(:,:,1) には x 軸方向の変位が格納されます。imwarp は、これらの値を D の列と行の位置に加算し、A における再マップ後の位置を生成します。同様に、D(:,:,2) には y 軸方向の変位が格納されます。

• A が m x n x c の 2 次元 RGB イメージまたは 2 次元 マルチスペクトル イメージで、なおかつ m x n x 2 の配列として D が指定されている場合、imwarp は、各 2 次元カラー チャネルに対して個別に処理を行います。D(:,:,1) には、すべてのカラー チャネルの x 軸方向の変位が格納されます。同様に、D(:,:,2) には y 軸方向の変位が格納されます。

• A が m x n x p の 3 次元グレースケール イメージの場合、m x n x p x 3 の配列として変位場配列を指定します。D(:,:,:,1) には x 軸方向の変位が格納されます。imwarp は、これらの値を D の列、行、および深さの位置に加算し、A における再マップ後の位置を生成します。同様に、D(:,:,:,2) と D(:,:,:,3) には y 軸方向と z 軸方向の変位が格納されます。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

RA — 変換されるイメージの空間参照情報

imref2d オブジェクト | imref3d オブジェクト

変換されるイメージの空間参照情報。2 次元変換の imref2d オブジェクトまたは 3 次元変換の imref3d オブジェクトとして指定されます。

interp — 使用される内挿のタイプ

"nearest" | "linear" | "cubic"

使用される内挿のタイプ。以下のいずれかの値を指定します。

内挿法	説明
"nearest"	最近傍内挿。出力ピクセルには、対象の点が含まれるピクセルの値が代入されます。周りの他のピクセルは、考慮に入れません。 最近傍内挿は、categorical イメージでサポートされている唯一のメソッドであり、このタイプのイメージに対する既定のメソッドです。
"linear"	線形内挿。線形内挿は、数値イメージと論理イメージに対する既定の内挿法です。
"cubic"	3 次内挿

データ型: char | string

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: B = imwarp(A,tform,FillValues=255) は 255 を塗りつぶしの値として使用します。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: B = imwarp(A,tform,"FillValues",255) は 255 を塗りつぶしの値として使用します。

OutputView — 出力イメージのサイズと位置

imref2d オブジェクト | imref3d オブジェクト

ワールド座標系における出力イメージのサイズと位置。imref2d または imref3d 空間参照オブジェクトとして指定します。このオブジェクトには、ワールド座標系における出力イメージのサイズと位置を定義するプロパティがあります。

関数 affineOutputView を使用することで、出力表示を作成できます。imwarp で計算される既定の出力表示を再現するには、affineOutputView の既定の境界のスタイル ("CenterOutput") を使用します。

入力の変位場 D を指定する場合、OutputView は指定できません。

FillValues — 塗りつぶしの値

数値スカラー | 数値配列 | string スカラー | 文字ベクトル | missing

入力イメージの外側にある出力ピクセルに使用する塗りつぶしの値。次の表のいずれかの値として指定します。imwarp は、入力イメージにおける対応する逆変換後の位置が完全に入力イメージの境界外である場合に、塗りつぶしの値を出力ピクセルに使用します。

数値イメージと論理イメージの既定の塗りつぶしの値は 0 です。categorical イメージの既定の塗りつぶしの値は missing です。<undefined> カテゴリに対応します。

イメージ タイプ	変換の次元	塗りつぶしの値の形式
2 次元グレースケール イメージまたは論理イメージ	2 次元	数値スカラー
2 次元カラー イメージまたは 2 次元マルチスペクトル イメージ	2 次元	数値スカラー c 要素の数値ベクトル。c チャネルのそれぞれに塗りつぶしの値を指定します。カラー イメージの場合、チャネル数 c は 3 です。
一連の p 2 次元イメージ	2 次元	数値スカラー c 行 p 列の数値行列。チャネル数 c は、グレースケール イメージの場合は 1 になり、カラー イメージの場合は 3 になります。
N 次元イメージ	2 次元	数値スカラー 入力イメージ A の 3 ～ N 次元に一致するサイズの数値配列。たとえば、A が 200 x 200 x 10 x 3 である場合、FillValues は 10 行 3 列の配列となります。
3 次元グレースケール イメージまたは論理イメージ	3 次元	数値スカラー
categorical イメージ	2 次元または 3 次元	イメージ内の有効なカテゴリ。string スカラーまたは文字ベクトルとして指定します。 missing。<undefined> カテゴリに対応します。詳細については、missing を参照してください。

例: 255 にすると、uint8 イメージを白のピクセルで塗りつぶします

例: 1 にすると、double イメージを白のピクセルで塗りつぶします

例: [0 1 0] にすると、double カラー イメージを緑のピクセルで塗りつぶします

例: [0 1 0; 0 1 1]' にすると、2 つの double カラー イメージから成るセットの場合、1 番目のイメージを緑のピクセルで、2 番目のイメージをシアンのピクセルで塗りつぶします

例: "vehicle" にすると、categorical イメージを "vehicle" カテゴリで塗りつぶします

SmoothEdges — 滑らかなエッジを作成するためのイメージのパディング

false (既定値) | true

滑らかなエッジを作成するためのイメージのパディング。true または false を指定します。true に設定すると、imwarp は FillValues で指定された値を使用して入力イメージをパディングすることで、滑らかなエッジを出力イメージに作成します。false に設定すると、imwarp はイメージをパディングしません。false (パディングなし) を選択すると、入力イメージによって出力イメージに鋭いエッジが生成される可能性があります。こうした鋭いエッジは、2 つのイメージを並べてレジストレーションする場合に継ぎ目の歪みを最小化するのに役立ちます。

出力引数

B — 変換されたイメージ

数値配列 | logical 配列 | categorical 配列

変換されたイメージ。入力イメージ A と同じデータ型の数値配列、logical 配列、または categorical 配列として返されます。

RB — 変換されたイメージの空間参照情報

imref2d オブジェクト | imref3d オブジェクト

変換されたイメージの空間参照情報。imref2d または imref3d の空間参照オブジェクトとして返されます。

アルゴリズム

imwarp は、出力イメージの位置を入力イメージの対応する位置にマッピングして (逆マッピング)、出力イメージのピクセルの値を決定します。出力イメージのピクセルの中心が入力イメージのピクセルの中心にマッピングされない場合、imwarp は入力イメージ内で内挿して出力ピクセル値を計算します。

次の図は、チェッカーボード イメージの平行移動変換を示しています。各正方形は 10 × 10 のピクセルです。規則により、入力空間の軸には "u" および "v"、出力空間の軸には "x" および "y" のラベルが付けられます。逆変換を使用して、出力座標空間の ("x", "y") 座標が (25, 35) のピクセルは、入力座標空間の ("u", "v") 座標 (5,5) にマッピングされます。

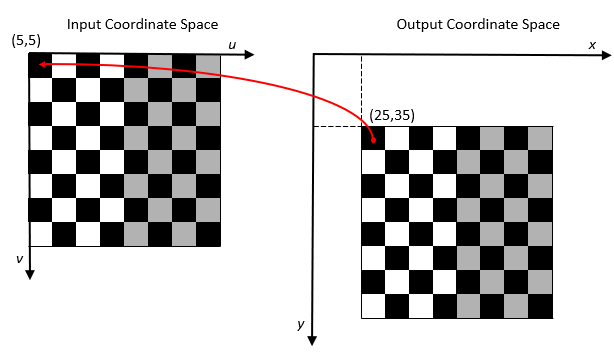
imwarp はワールド座標を使用してマッピングを実行します。詳細については、イメージの座標系を参照してください。

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• imwarp では C コードの生成がサポートされています (MATLAB^® Coder™ が必要)。汎用の MATLAB Host Computer ターゲット プラットフォームを選択した場合、プリコンパイルされたプラットフォーム固有の共有ライブラリを使用するコードが、imwarp によって生成されます。共有ライブラリを使用するとパフォーマンスの最適化は維持されますが、コードを生成できるターゲット プラットフォームが限定されます。詳細については、Image Processing Toolbox でサポートされているコード生成のタイプを参照してください。

• データ型 categorical の入力イメージはサポートされていません。

• 幾何学的変換オブジェクトの入力 tform は、2 次元幾何学的変換を表していなければなりません。

• 内挿法とオプションのパラメーター名は定数でなければなりません。

GPU コード生成

GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

使用上の注意および制限:

• データ型 categorical の入力イメージはサポートされていません。

• 幾何学的変換オブジェクトの入力 tform は、2 次元幾何学的変換を表していなければなりません。

• 内挿法とオプションのパラメーター名は定数でなければなりません。

• 空間参照情報出力 RB はサポートされません。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数は、スレッドベースの環境を完全にサポートします。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

使用上の注意および制限:

• "nearest" および "linear" の内挿タイプのみがサポートされます。

• SmoothEdges 引数の値としてサポートされているのは false のみです。

詳細については、GPU でのイメージ処理を参照してください。

バージョン履歴

R2013a で導入

R2022b: 新しい幾何学的変換オブジェクトをサポート

R2022b 以降、ほとんどの Image Processing Toolbox™ 関数は、左から乗算する規則を使用して幾何学的変換を作成し、実行します。そのため、tform を、affinetform2d オブジェクトなどの左から乗算する規則を使用する幾何学的変換オブジェクトとして指定できるようになりました。

tform は、affine2d オブジェクトなどの、右から乗算する規則を使用する幾何学的変換オブジェクトとして指定することもできますが、これらのオブジェクトは推奨されません。左から乗算する新しい幾何学的変換オブジェクトに切り替えることで、幾何学的変換のワークフローを効率化できます。詳細については、Migrate Geometric Transformations to Premultiply Conventionを参照してください。

R2021b: スレッドベース環境のサポート

imwarp は、スレッドベースの環境をサポートするようになりました。

R2021a: GPU による高速化のサポート強化

関数 imwarp は GPU による高速化を既にサポートしていますが、変位場の使用を含めるようにサポートが拡張されました。

参考

アプリ

• レジストレーション推定

関数

• affineOutputView | imregister | imregtform | imregdemons | imtranslate | randomWindow2d | centerCropWindow2d

トピック

• 2 次元および 3 次元の幾何学的変換プロセスの概要

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい