compareHoldout

新しいデータを使用して 2 つの分類モデルの精度を比較

構文

h = compareHoldout(C1,C2,T1,T2,ResponseVarName)

h = compareHoldout(C1,C2,T1,T2,Y)

h = compareHoldout(C1,C2,X1,X2,Y)

h = compareHoldout(___,Name,Value)

[h,p,e1,e2] = compareHoldout(___)

説明

compareHoldout は、2 つの分類モデルの精度を統計的に評価します。この関数では、予測したラベルを真のラベルに対して比較してから、誤分類率の違いが統計的に有意であるかどうかを調べます。

複数の分類モデルの精度が異なるかどうかや、あるモデルの性能が別のモデルより優れているかどうかを判断できます。compareHoldout では、漸近検定、厳密条件検定、mid-p 値検定など、いくつかのマクネマー検定のバリエーションを実行できます。コストを考慮する評価については、カイ二乗検定 (Optimization Toolbox™ が必要) や尤度比検定などの検定を行うことができます。

h = compareHoldout(C1,C2,T1,T2,ResponseVarName) は、「学習済みの分類モデル C1 および C2 は変数 ResponseVarName に含まれている真のクラス ラベルを予測する精度が等しい」という帰無仮説の検定の判定を返します。対立仮説は「ラベルの精度は等しくない」です。

1 番目の分類モデル C1 では T1 に含まれている予測子データを、2 番目の分類モデル C2 では T2 に含まれている予測子データを使用します。table T1 および T2 には、同じ応答変数を含めなければなりませんが、予測子については異なるセットを含めることができます。既定では、mid-p 値マクネマー検定が精度の比較に使用されます。

h = 1 の場合、帰無仮説は 5% の有意水準で棄却されます。h = 0 の場合、帰無仮説は 5% の水準では棄却されません。

以下のような検定を行うことができます。

• 同じ予測子データのセットを渡して (T1 = T2)、単純な分類モデルとより複雑なモデルの精度を比較する。

• 異なる可能性がある 2 種類の予測子データのセットを使用して、異なる可能性がある 2 つのモデルの精度を比較する。

• さまざまな特徴選択を実行する。たとえば、ある予測子のセットを使用して学習させたモデルの精度と、同じ予測子のサブセットまたは別の予測子のセットを使用して学習させたモデルの精度を比較できます。予測子のセットは自由に選択できます。また、PCA (pca 参照) や逐次特徴選択 (sequentialfs 参照) などの特徴選択手法を使用することもできます。

h = compareHoldout(C1,C2,T1,T2,Y) は、学習済みの分類モデル C1 および C2 は真のクラス ラベル Y を予測する精度が等しいという帰無仮説の検定の判定を返します。対立仮説は「ラベルの精度は等しくない」です。

1 番目の分類モデル C1 では予測子データ T1 を、2 番目の分類モデル C2 では予測子データ T2 を使用します。既定では、mid-p 値マクネマー検定が精度の比較に使用されます。

h = compareHoldout(C1,C2,X1,X2,Y) は、学習済みの分類モデル C1 および C2 は真のクラス ラベル Y を予測する精度が等しいという帰無仮説の検定の判定を返します。対立仮説は「ラベルの精度は等しくない」です。

1 番目の分類モデル C1 では予測子データ X1 を、2 番目の分類モデル C2 では予測子データ X2 を使用します。既定では、mid-p 値マクネマー検定が精度の比較に使用されます。

h = compareHoldout(___,Name,Value) では、前の構文の入力引数の組み合わせに加えて、1 つ以上の名前と値のペアの引数を使用してオプションを指定します。たとえば、対立仮説のタイプ、検定のタイプ、コスト行列を指定できます。

[h,p,e1,e2] = compareHoldout(___) は、前の構文のいずれかの入力引数を使用して、仮説検定の p 値 (p) と、予測したクラス ラベルの各セットに対応する 分類損失 (e1 および e2) を返します。

例

完全な分類モデルと縮小した分類モデルの精度の比較

2 つの k 最近傍分類器に学習をさせます。一方の分類器では、もう一方で使用した予測子のサブセットを使用します。テスト セットで 2 つのモデルの精度を比較する統計検定を実行します。

carsmall データ セットを読み込みます。

load carsmall

2 つの入力データの table を作成します。2 番目の table では予測子 Acceleration を除外します。応答変数として Model_Year を指定します。

T1 = table(Acceleration,Displacement,Horsepower,MPG,Model_Year);
T2 = T1(:,2:end);

データを学習セットとテスト セットに分割します。データの 30% をテスト用に確保します。

rng(1)  % For reproducibility
CVP = cvpartition(Model_Year,'holdout',0.3);
idxTrain = training(CVP);   % Training-set indices
idxTest = test(CVP);    % Test-set indices

CVP は、学習セットとテスト セットを指定する交差検証分割オブジェクトです。

T1 と T2 のデータを使用して ClassificationKNN モデルに学習をさせます。

C1 = fitcknn(T1(idxTrain,:),'Model_Year');
C2 = fitcknn(T2(idxTrain,:),'Model_Year');

C1 と C2 は学習済みの ClassificationKNN モデルです。

テスト セットで 2 つのモデルの予測精度が等しいかどうかをテストします。

h = compareHoldout(C1,C2,T1(idxTest,:),T2(idxTest,:),'Model_Year')

h = logical
   0

h = 0 なので、2 つのモデルの予測精度が等しいという帰無仮説は棄却できません。

2 つの異なる分類モデルの精度を比較する

異なるアルゴリズムを使用して 2 つの分類モデルを学習させます。テスト セットで 2 つのモデルの誤分類率を比較する統計検定を実行します。

ionosphere データ セットを読み込みます。

load ionosphere

データを学習セットとテスト セットに均等に分割します。

rng(1)                             % For reproducibility
CVP = cvpartition(Y,'holdout',0.5);
idxTrain = training(CVP);           % Training-set indices 
idxTest = test(CVP);                % Test-set indices

CVP は、学習セットとテスト セットを指定する交差検証分割オブジェクトです。

SVM モデルと、バギング分類木が 100 本あるアンサンブルを学習させます。SVM モデルについては、放射基底関数カーネルとヒューリスティック手法を使用してカーネル スケールを決定するように指定します。

C1 = fitcsvm(X(idxTrain,:),Y(idxTrain),'Standardize',true, ...
    'KernelFunction','RBF','KernelScale','auto');
t = templateTree('Reproducible',true);  % For reproducibility of random predictor selections
C2 = fitcensemble(X(idxTrain,:),Y(idxTrain),'Method','Bag', ...
    'Learners',t);

C1 は学習済みの ClassificationSVM モデルです。C2 は学習済みの ClassificationBaggedEnsemble モデルです。

2 つのモデルの予測精度が同じであるかどうかを検定します。各モデルについて同じテスト セット予測子データを使用します。

h = compareHoldout(C1,C2,X(idxTest,:),X(idxTest,:),Y(idxTest))

h = logical
   0

h = 0 なので、2 つのモデルの予測精度が等しいという帰無仮説は棄却できません。

より複雑なモデルに対する分類モデルの比較

同じアルゴリズムを使用して 2 つの分類モデルを学習させます。ただし、ハイパーパラメーターを調整してアルゴリズムをより複雑にします。複雑なモデルより単純なモデルの方がテスト データに対する精度が優れているかどうかを評価する統計検定を実行します。

ionosphere データ セットを読み込みます。

load ionosphere;

データを学習セットとテスト セットに均等に分割します。

rng(1);                             % For reproducibility
CVP = cvpartition(Y,'holdout',0.5);
idxTrain = training(CVP);           % Training-set indices 
idxTest = test(CVP);                % Test-set indices

CVP は、学習セットとテスト セットを指定する交差検証分割オブジェクトです。

線形カーネル (バイナリ分類の既定) を使用する SVM モデルと放射基底関数カーネルを使用する SVM モデルを学習させます。カーネル スケールには、既定値の 1 を使用します。

C1 = fitcsvm(X(idxTrain,:),Y(idxTrain),'Standardize',true);
C2 = fitcsvm(X(idxTrain,:),Y(idxTrain),'Standardize',true,...
    'KernelFunction','RBF');

C1 と C2 は学習済みの ClassificationSVM モデルです。

単純なモデル (C1) の精度は複雑なモデル (C2) の精度と同程度であるという帰無仮説を検定します。テスト セットのサイズが大きいので、漸近マクネマー検定を実行し、mid-p 値検定 (コストを考慮しない検定の既定) で結果を比較します。p 値と誤分類率を返すように指定します。

Asymp = zeros(4,1); % Preallocation
MidP = zeros(4,1); 

[Asymp(1),Asymp(2),Asymp(3),Asymp(4)] = compareHoldout(C1,C2,...
    X(idxTest,:),X(idxTest,:),Y(idxTest),'Alternative','greater',...
    'Test','asymptotic');
[MidP(1),MidP(2),MidP(3),MidP(4)] = compareHoldout(C1,C2,...
    X(idxTest,:),X(idxTest,:),Y(idxTest),'Alternative','greater');
table(Asymp,MidP,'RowNames',{'h' 'p' 'e1' 'e2'})

ans=4×2 table
            Asymp          MidP   
          __________    __________

    h              1             1
    p     7.2801e-09    2.7649e-10
    e1       0.13714       0.13714
    e2       0.33143       0.33143

両方の検定で p 値がゼロに近いので、単純なモデルの精度が複雑なモデルの精度より低いという帰無仮説を棄却するだけの十分な証拠が得られました。どの検定を指定しても、compareHoldout は両方のモデルについて同じタイプの誤分類尺度を返します。

コストを考慮して 2 つの分類モデルを比較する

データ セットのクラスの表現が不均衡である場合、または偽陽性のコストと偽陰性のコストが不均衡である場合、コスト行列を分析に含めることにより、2 つの分類モデルの予測性能を統計的に比較できます。

arrhythmia データ セットを読み込みます。データのクラス表現を判別します。

load arrhythmia;
Y = categorical(Y);
tabulate(Y);

  Value    Count   Percent
      1      245     54.20%
      2       44      9.73%
      3       15      3.32%
      4       15      3.32%
      5       13      2.88%
      6       25      5.53%
      7        3      0.66%
      8        2      0.44%
      9        9      1.99%
     10       50     11.06%
     14        4      0.88%
     15        5      1.11%
     16       22      4.87%

16 個のクラスがありますが、一部はデータ セットで表現されていません (たとえば、クラス 13)。ほとんどの観測値は不整脈がないものとして分類されています (クラス 1)。このデータ セットは非常に離散的であり、クラスが不均衡です。

不整脈があるすべての観測値 (クラス 2 ～ 15) を 1 つのクラスに結合します。不整脈の状況 (クラス 16) が不明である観測値をデータ セットから削除します。

idx = (Y ~= '16');
Y = Y(idx);
X = X(idx,:);
Y(Y ~= '1') = 'WithArrhythmia';
Y(Y == '1') = 'NoArrhythmia';
Y = removecats(Y);

データを学習セットとテスト セットに均等に分割します。

rng(1);                             % For reproducibility
CVP = cvpartition(Y,'holdout',0.5);
idxTrain = training(CVP);           % Training-set indices 
idxTest = test(CVP);                % Test-set indices

CVP は、学習セットとテスト セットを指定する交差検証分割オブジェクトです。

コスト行列を作成します。不整脈がある患者を不整脈なしのクラスに誤分類した場合はコストを高くし、不整脈がない患者を不整脈ありのクラスに誤分類した場合の 5 倍にします。正しく分類した場合、コストは発生しません。行は真のクラスを、列は予測したクラスを表します。コストを考慮する分析を実行するときは、クラスの順序を指定することをお勧めします。

cost = [0 1;5 0];
ClassNames = {'NoArrhythmia','WithArrhythmia'};

50 本の分類木がある 2 つのブースティング アンサンブルに学習をさせます。一方では AdaBoostM1 を、もう一方では LogitBoost を使用します。欠損値がデータ セットに含まれているので、代理分岐を使用するように指定します。コスト行列を使用してモデルを学習させます。

t = templateTree('Surrogate','on');
numTrees = 50;
C1 = fitcensemble(X(idxTrain,:),Y(idxTrain),'Method','AdaBoostM1', ...
    'NumLearningCycles',numTrees,'Learners',t, ...
    'Cost',cost,'ClassNames',ClassNames);
C2 = fitcensemble(X(idxTrain,:),Y(idxTrain),'Method','LogitBoost', ...
    'NumLearningCycles',numTrees,'Learners',t, ...
    'Cost',cost,'ClassNames',ClassNames);

C1 と C2 は学習済みの ClassificationEnsemble モデルです。

関数 loss を使用してテスト データの分類損失を計算します。LossFun を 'classifcost' と指定して誤分類コストを計算します。

L1 = loss(C1,X(idxTest,:),Y(idxTest),'LossFun','classifcost')

L1 = 
0.6642

L2 = loss(C2,X(idxTest,:),Y(idxTest),'LossFun','classifcost')

L2 = 
0.8018

AdaBoostM1 アンサンブル (C1) の誤分類コストの方が LogitBoost アンサンブル (C2) のコストよりも小さくなっています。

この違いが統計的に有意であるかどうかを検定します。コストを考慮する漸近的な尤度比検定 (コスト行列を渡す場合の既定) を実行します。コスト行列を与えて、"p" 値と誤分類コストを返します。

[h,p,e1,e2] = compareHoldout(C1,C2,X(idxTest,:),X(idxTest,:),Y(idxTest),...
    'Cost',cost,'ClassNames',ClassNames)

h = logical
   0

p = 
0.1180

e1 = 
0.6698

e2 = 
0.8093

h = 0 なので、2 つのモデルの予測精度が等しいという帰無仮説は棄却できません。

関数 loss は事前確率 (学習済みモデルの Prior プロパティに格納) で正規化された観測値の重みを使用しますが、関数 compareHoldout は観測値の重みと事前確率を使用しません。そのため、関数 loss で計算される誤分類コストの値 (L1 および L2) は、関数 compareHoldout で計算される値 (e1 および e2) と異なる場合があります。

統計的な精度比較による特徴量の選択

予測子変数 (特徴量) のサブセットをより大きいセットから選択して、分類モデルの複雑さを減らします。そして、2 つのモデルの標本外精度を統計的に比較します。

ionosphere データ セットを読み込みます。

load ionosphere;

データを学習セットとテスト セットに均等に分割します。

rng(1);  % For reproducibility
CVP = cvpartition(Y,'holdout',0.5);
idxTrain = training(CVP); % Training-set indices 
idxTest = test(CVP);      % Test-set indices

CVP は、学習セットとテスト セットを指定する交差検証分割オブジェクトです。

AdaBoostM1 とすべての予測子セットを使用して、100 個のブースティング分類木があるアンサンブルを学習させます。各予測子について重要度を調べます。

t = templateTree('MaxNumSplits',1); % Weak-learner template tree object
C2 = fitcensemble(X(idxTrain,:),Y(idxTrain),'Method','AdaBoostM1',...
    'Learners',t);
predImp = predictorImportance(C2);

figure;
bar(predImp);
h = gca;
h.XTick = 1:2:h.XLim(2)

h = 
  Axes with properties:

             XLim: [-0.2000 35.2000]
             YLim: [0 0.0090]
           XScale: 'linear'
           YScale: 'linear'
    GridLineStyle: '-'
         Position: [0.1300 0.1100 0.7750 0.8150]
            Units: 'normalized'

  Show all properties

title('Predictor Importance');
xlabel('Predictor');
ylabel('Importance measure');

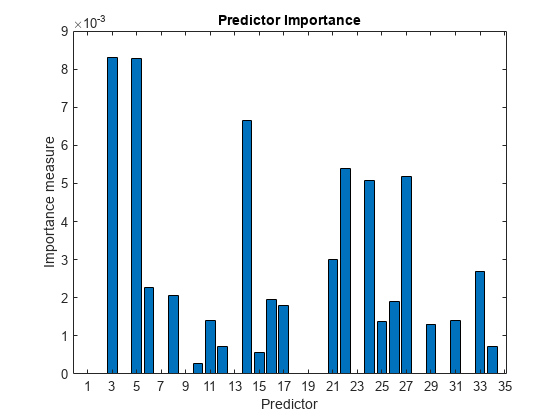
重要度が上位 5 番目までの予測子を識別します。

[~,idxSort] = sort(predImp,'descend');
idx5 = idxSort(1:5);

AdaBoostM1 と上位 5 番目までの重要度をもつ予測子を使用して、100 本のブースティング分類木がある別のアンサンブルに学習をさせます。

C1 = fitcensemble(X(idxTrain,idx5),Y(idxTrain),'Method','AdaBoostM1',...
    'Learners',t);

2 つのモデルの予測精度が同じであるかどうかを検定します。C1 には縮小したテスト セット予測子データを、C2 には完全なテスト セット予測子データを指定します。

[h,p,e1,e2] = compareHoldout(C1,C2,X(idxTest,idx5),X(idxTest,:),Y(idxTest))

h = logical
   0

p = 
0.7744

e1 = 
0.0914

e2 = 
0.0857

h = 0 なので、2 つのモデルの予測精度が等しいという帰無仮説は棄却できません。この結果から、単純なアンサンブル C1 の方が有利であることがわかります。

入力引数

C1 — 1 番目の学習済み分類モデル

学習済みの分類モデル オブジェクト | 学習済みのコンパクトな分類モデル オブジェクト

1 番目の学習済み分類モデル。次の表に記載されている学習済み分類モデル オブジェクトまたはコンパクトな分類モデル オブジェクトを指定します。

学習済みモデルのタイプ	モデル オブジェクト	生成元
分類木	ClassificationTree	fitctree
判別分析	ClassificationDiscriminant	fitcdiscr
バギングされた分類モデルのアンサンブル	ClassificationBaggedEnsemble	fitcensemble
分類モデルのアンサンブル	ClassificationEnsemble	fitcensemble
マルチクラスの誤り訂正出力符号 (ECOC)	ClassificationECOC	fitcecoc
一般化加法モデル (GAM)	ClassificationGAM	fitcgam
kNN	ClassificationKNN	fitcknn
単純ベイズ	ClassificationNaiveBayes	fitcnb
ニューラル ネットワーク	ClassificationNeuralNetwork (行に観測値が含まれる)	fitcnet
サポート ベクター マシン (SVM)	ClassificationSVM	fitcsvm
コンパクトな判別分析	CompactClassificationDiscriminant	compact
コンパクトな ECOC	CompactClassificationECOC	compact
コンパクトな分類モデルのアンサンブル	CompactClassificationEnsemble	compact
コンパクトな GAM	CompactClassificationGAM	compact
コンパクトな単純ベイズ	CompactClassificationNaiveBayes	compact
コンパクトなニューラル ネットワーク	CompactClassificationNeuralNetwork	compact
コンパクトな SVM	CompactClassificationSVM	compact
コンパクトな分類木	CompactClassificationTree	compact

C2 — 2 番目の学習済み分類モデル

学習済みの分類モデル オブジェクト | 学習済みのコンパクトな分類モデル オブジェクト

2 番目の学習済み分類モデル。C1 の選択肢として有効である学習済み分類モデル オブジェクトまたはコンパクトな分類モデル オブジェクトを指定します。

T1 — 1 番目の分類モデルのテスト セット予測子データ

table

1 番目の分類モデル C1 におけるテスト セット予測子データ。table を指定します。T1 の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。オプションとして、応答変数用の追加列を T1 に含めることができます。T1 には、C1 を学習させるために使用したすべての予測子が含まれていなければなりません。文字ベクトルの cell 配列ではない cell 配列と複数列の変数は使用できません。

T1 と T2 の行および応答値は、同数でなければなりません。C1 と C2 に学習をさせるために使用した応答変数が T1 と T2 に含まれている場合、ResponseVarName または Y を指定する必要はありません。

データ型: table

T2 — 2 番目の分類モデルのテスト セット予測子データ

table

2 番目の分類モデル C2 におけるテスト セット予測子のテーブル。テーブルとして指定します。T2 の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。オプションとして、応答変数用の追加列を T2 に含めることができます。T2 には、C2 を学習させるために使用したすべての予測子が含まれていなければなりません。文字ベクトルの cell 配列ではない cell 配列と複数列の変数は使用できません。

T1 と T2 の行および応答値は、同数でなければなりません。C1 と C2 に学習をさせるために使用した応答変数が T1 と T2 に含まれている場合、ResponseVarName または Y を指定する必要はありません。

データ型: table

X1 — 1 番目の分類モデルのテスト セット予測子データ

数値行列

1 番目の分類モデル C1 のテスト セット予測子データ。数値行列を指定します。

X1 の各行は 1 つの観測値 (インスタンスまたは事例とも呼ぶ) に、各列は 1 つの変数 (予測子または特徴とも呼ぶ) に対応しています。X1 は、C1 を学習させるために使用した変数で構成しなければなりません。

X1 と X2 の行数は Y の行数と等しくなければなりません。

データ型: double | single

X2 — 2 番目の分類モデルのテスト セット予測子データ

数値行列

2 番目の分類モデル C2 のテスト セット予測子データ。数値行列を指定します。

X2 の各行は 1 つの観測値 (インスタンスまたは事例とも呼ぶ) に、各列は 1 つの変数 (予測子または特徴とも呼ぶ) に対応しています。X2 は、C2 を学習させるために使用した変数で構成しなければなりません。

X2 と X1 の行数は Y の行数と等しくなければなりません。

データ型: double | single

ResponseVarName — 応答変数名

T1 および T2 内にある変数の名前

応答変数名。T1 および T2 内にある変数の名前を指定します。C1 と C2 を学習させるために使用した応答変数が T1 と T2 に含まれている場合、ResponseVarName を指定する必要はありません。

ResponseVarName には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、応答変数が T1.Response として格納されている場合、'Response' として指定します。それ以外の場合、T1 と T2 の列は Response を含めてすべて予測子として扱われます。

応答変数は、categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列でなければなりません。応答変数が文字配列の場合、各要素は配列の 1 つの行に対応しなければなりません。

データ型: char | string

Y — 真のクラス ラベル

categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

真のクラス ラベル。categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列を指定します。

Y を指定するときに、compareHoldout は行列 X1 および X2 または table T1 および T2 内のすべての変数を予測子変数として扱います。

Y が文字配列の場合、各要素は配列の 1 つの行に対応しなければなりません。

予測子データの行数は Y の行数と等しくなければなりません。

データ型: categorical | char | string | logical | single | double | cell

メモ

NaN、<undefined> 値、空の文字ベクトル ('')、空の string ("")、および <missing> 値は、欠損値を示します。compareHoldout は、Y の欠損値と X1 および X2 の対応する行の欠損値を削除します。さらに、X1 と X2 に欠損観測値が含まれている場合でも compareHoldout はクラスを予測します。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: compareHoldout(C1,C2,X1,X2,Y,'Alternative','greater','Test','asymptotic','Cost',[0 2;1 0]) は、1 番目の予測クラス ラベルのセットが 2 番目のセットより正確であるかどうかを検定し、漸近的なマクネマー検定を実行し、真のラベルが ClassNames{1} である観測値を誤分類するペナルティを真のラベルが ClassNames{2} である観測値の場合の 2 倍にします。

Alpha — 仮説検定の有意水準

0.05 (既定値) | (0, 1) の範囲にあるスカラー値

仮説検定の有意水準。'Alpha' と (0, 1) の範囲にあるスカラー値をコンマで区切って指定します。

例: 'Alpha',0.1

データ型: single | double

Alternative — 評価する対立仮説

'unequal' (既定値) | 'greater' | 'less'

評価する対立仮説。'Alternative' と次の表に記載されている値のいずれかから構成されるコンマ区切りのペアとして指定します。

値	対立仮説
'unequal' (既定の設定)	Y を予測する場合、X1 に C1 を適用して生成された予測と X2 に C2 を適用して生成された予測では精度が異なる。
'greater'	Y を予測する場合、X1 に C1 を適用して生成された予測は X2 に C2 を適用して生成された予測より精度が高い。
'less'	Y を予測する場合、X1 に C1 を適用して生成された予測は X2 に C2 を適用して生成された予測より精度が低い。

例: 'Alternative','greater'

ClassNames — クラス名

categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

クラス名。'ClassNames' と categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列から構成されるコンマ区切りのペアとして指定します。ClassNames は Y のデータ型を使用して設定しなければなりません。

ClassNames が文字配列の場合、各要素は配列の 1 つの行に対応しなければなりません。

ClassNames の使用目的は次のとおりです。

• クラスの順序に対応する入力引数の次元の順序を指定する。たとえば、Cost の次元の順序を指定するために ClassNames を使用します。

• 検定用にクラスのサブセットを選択する。たとえば、Y に含まれているすべての異なるクラス名の集合が {'a','b','c'} であるとします。クラス 'a' および 'c' のみの観測値を使用してモデルの学習と検定を行うには、'ClassNames',{'a','c'} を指定します。

既定の設定は、Y に含まれているすべての異なるクラス名の集合です。

例: 'ClassNames',{'b','g'}

データ型: categorical | char | string | logical | single | double | cell

Cost — 誤分類のコスト

正方行列 | 構造体配列

誤分類のコスト。'Cost' と正方行列または構造体配列をコンマで区切って指定します。

• 正方行列 Cost を指定する場合、Cost(i,j) は真のクラスが i の点をクラス j に分類するコストです。つまり、行は真のクラスに、列は予測するクラスに対応します。Cost の対応する行および列についてクラスの順序を指定するには、名前と値のペアの引数 ClassNames をさらに指定します。

• 構造体 S を指定する場合、S には次の 2 つのフィールドが必要です。

  • S.ClassNames。Y と同じデータ型の変数としてクラス名を格納します。このフィールドを使用してクラスの順序を指定できます。

  • S.ClassificationCosts。行と列の順序が S.ClassNames と同じであるコスト行列。

Cost を指定した場合、compareHoldout では片側検定、厳密検定および mid-p 検定を実行できません。'Alternative','unequal','Test','asymptotic' も指定しなければなりません。コストを考慮する検定のオプションについては、名前と値のペアの引数 CostTest を参照してください。

分類モデルに学習をさせるために使用したものと同じコスト行列を渡すことをお勧めします。

既定値は、i ~= j の場合は Cost(i,j) = 1、i = j の場合は Cost(i,j) = 0 です。

例: 'Cost',[0 1 2 ; 1 0 2; 2 2 0]

データ型: single | double | struct

CostTest — コストを考慮する検定のタイプ

'likelihood' (既定値) | 'chisquare'

コストを考慮する検定のタイプ。'CostTest' と 'chisquare' または 'likelihood' をコンマ区切りのペアとして指定します。名前と値のペアの引数 Cost によるコスト行列の指定を行わなかった場合、compareHoldout は CostTest を無視します。

次の表に、コストを考慮する検定で利用できるオプションの概要を示します。

値	漸近検定のタイプ	要件
'chisquare'	カイ二乗検定	quadprog (Optimization Toolbox) を実装するための Optimization Toolbox
'likelihood'	尤度比検定	なし

詳細は、コストを考慮する検定を参照してください。

例: 'CostTest','chisquare'

Test — 実行する検定

'asymptotic' | 'exact' | 'midp'

実行する検定。'Test' と 'asymptotic'、'exact' または 'midp' から構成されるコンマ区切りのペアとして指定します。

次の表に、コストを考慮しない検定で利用できるオプションの概要を示します。

値	説明
'asymptotic'	漸近的なマクネマー検定
'exact'	厳密条件マクネマー検定
'midp' (既定の設定)	mid-p 値マクネマー検定

詳細は、マクネマー検定を参照してください。

コストを考慮する検定の場合、Test は 'asymptotic' でなければなりません。名前と値のペアの引数 Cost を指定し、名前と値のペアの引数 CostTest を使用してコストを考慮する検定を選択した場合、既定は 'asymptotic' です。

例: 'Test','asymptotic'

出力引数

h — 仮説検定の結果

1 | 0

論理値として返される仮説検定の結果。

h = 1 の場合、有意水準 Alpha で帰無仮説が棄却されます。

h = 0 の場合、有意水準 Alpha では帰無仮説を棄却できません。

データ型: logical

p — p 値

[0,1] の範囲にあるスカラー値

検定の p 値。[0,1] の範囲にあるスカラー値として返されます。p は、帰無仮説が真であると仮定した場合に、観測された検定統計量よりも無作為な検定統計量の方が極端な値になる確率です。

compareHoldout では、検定のタイプによって異なる検定統計量の分布を使用して p を推定します。マクネマー検定のバリエーションから導き出される検定統計量についての詳細は、マクネマー検定を参照してください。コストを考慮する検定から導き出される検定統計量についての詳細は、コストを考慮する検定を参照してください。

データ型: double

e1 — 分類損失

数値スカラー

分類損失。数値スカラーとして返されます。e1 は、1 番目のクラス ラベルのセットが真のクラス ラベル (Y) を予測する精度を要約します。compareHoldout は、1 番目のテスト セットの予測子データ (X1) を 1 番目の分類モデル (C1) に適用して、1 番目のクラス ラベルのセットを評価します。そして、推定したラベルを Y と比較して分類損失を取得します。

コストを考慮しない検定の場合、e1 は誤分類率です。つまり、e1 は誤分類した観測値の比率であり、[0,1] の範囲にあるスカラー値になります。

コストを考慮する検定の場合、e1 は誤分類コストです。つまり、e1 は誤分類コストの加重平均です。この場合の重みは、誤分類した観測値についてそれぞれ推定した比率です。

詳細は、分類損失を参照してください。

データ型: double

e2 — 分類損失

数値スカラー

分類損失。数値スカラーとして返されます。e2 は、2 番目のクラス ラベルのセットが真のクラス ラベル (Y) を予測する精度を要約します。compareHoldout は、2 番目のテスト セットの予測子データ (X2) を 2 番目の分類モデル (C2) に適用して、2 番目のクラス ラベルのセットを評価します。そして、推定したラベルを Y と比較して分類損失を取得します。

コストを考慮しない検定の場合、e2 は誤分類率です。つまり、e2 は誤分類した観測値の比率であり、[0,1] の範囲にあるスカラー値になります。

コストを考慮する検定の場合、e2 は誤分類コストです。つまり、e2 は誤分類コストの加重平均です。この場合の重みは、誤分類した観測値についてそれぞれ推定した比率です。

詳細は、分類損失を参照してください。

データ型: double

制限

• compareHoldout は、線形分類モデルまたはカーネル分類モデル (つまり ClassificationLinear または ClassificationKernel モデル オブジェクト) から構成される ECOC モデルを比較しません。線形分類モデルまたはカーネル分類モデルから構成される ClassificationECOC モデルを比較するには、代わりに testcholdout を使用します。

• 同様に、compareHoldout は ClassificationLinear または ClassificationKernel モデル オブジェクトを比較しません。これらのモデルを比較するには、代わりに testcholdout を使用します。

詳細

コストを考慮する検定

"コストを考慮する検定" は、誤分類のコストが不均衡な場合に実行します。コストを考慮する分析を実行することにより、分類モデルに学習をさせるときと、これらを統計的に比較するときに、コストの不均衡を考慮できます。

誤分類のコストが不均衡な場合、誤分類率では分類損失の性能が低下する傾向があります。代わりに誤分類コストを使用して分類モデルを比較します。

誤分類コストは、多くの用途で不均衡になります。たとえば、一連の予測子に基づいて被験者を健康および病気という 2 つのカテゴリに分類するとします。病気の被験者を健康として誤分類すると、被験者の生命に危険がもたらされます。しかし、健康な被験者を病気として誤分類しても、一般に不都合は生じますが、著しく危険なわけではありません。このような状況では、健康な被験者を病気として誤分類した場合より病気の被験者を健康として誤分類した場合の方がコストが高くなるように誤分類コストを割り当てます。

以下の定義では、コストを考慮する検定の概要について説明します。この定義では次のようにします。

• n_ijk および $${\widehat{\pi }}_{ijk}$$ は、次の特徴をもつ検定標本観測値の個数および推定比率です。k は真のクラス、i は 1 番目の分類モデルによって割り当てられたラベル、j は 2 番目の分類モデルによって割り当てられたラベルです。$${\widehat{\pi }}_{ijk}$$ の不明な真の値は π_ijk です。テスト セットの標本サイズは $$\sum _{i,j,k}{n}_{ijk}=n_{test}.$$ です。また、$$\sum _{i,j,k}{\pi }_{ijk}=\sum _{i,j,k}{\widehat{\pi }}_{ijk}=1.$$ です。

• c_ij は、真のクラスが i である観測値にラベル j を割り当てる相対的なコストです。c_ii = 0、c_ij ≥ 0 であり、少なくとも 1 つの (i,j) のペアで c_ij > 0 です。

• すべての添字は、1 から K (クラスの数) までの整数値です。

• 2 つの分類モデルの誤分類コストについて予想される差は、次のようになります。

  $$\delta ={\displaystyle \sum _{i=1}^K{\displaystyle \sum _{j=1}^K{\displaystyle \sum }_{k=1}^K\left(c_{ki}-c_{kj}\right){\pi }_{ijk}}}.$$

• 仮説検定は次のようになります。

  $$\begin{array}{c}{H}_0:\delta =0\\ H_1:\delta \ne 0\end{array}.$$

  コストを考慮する検定として使用できる検定は、両側検定に適しています。

不均衡なコストに対処する漸近検定として、"カイ二乗検定" と "尤度比検定" を使用できます。

• カイ二乗検定 ― カイ二乗検定統計量はピアソンとネイマンのカイ二乗検定統計量に基づいていますが、n_ijk = 0 の場合を考慮するラプラスの補正因子が含まれています。検定統計量は次のようになります。

  $$t_{{\chi }^2}^{\ast }=\sum _{i\ne j}\sum _k\frac{{\left(n_{ijk}+1-\left(n_{test}+K^3\right){\widehat{\pi }}_{ijk}^{(1)}\right)}^2}{n_{ijk}+1}.$$

  $$1-F_{{\chi }^2}\left(t_{{\chi }^2}^{\ast };1\right)<\alpha$$ である場合、H₀ は棄却されます。

  • $${\widehat{\pi }}_{ijk}^{(1)}$$ は、δ = 0 という制約で $$t_{{\chi }^2}^{\ast }$$ を最小化することにより推定されます。

  • $$F_{{\chi }^2}(x;1)$$ は、x で評価した自由度 1 の χ² 累積分布関数です。

• 尤度比検定 — 尤度比検定は、標本サイズが n_test、成功確率が π_ijk の二項確率変数である N_ijk に基づいています。この確率変数は、真のクラスが k、1 番目の分類モデルによって割り当てられたラベルが i、2 番目の分類モデルによって割り当てられたラベルが j である観測値である乱数を表します。合わせることで、この確率変数の分布は多項分布になります。

  検定統計量は次のようになります。

  $$t_{LRT}^{\ast }=2\log \left[\frac{P\left(\underset{i,j,k}{\cap }{N}_{ijk}=n_{ijk};n_{test},{\widehat{\pi }}_{ijk}={\widehat{\pi }}_{ijk}^{(2)}\right)}{P\left(\underset{i,j,k}{\cap }{N}_{ijk}=n_{ijk};n_{test},{\widehat{\pi }}_{ijk}={\widehat{\pi }}_{ijk}^{(3)}\right)}\right].$$

  $$1-F_{{\chi }^2}\left(t_{LRT}^{\ast };1\right)<\alpha ,$$ である場合、H₀ は棄却されます。

  • $${\widehat{\pi }}_{ijk}^{(2)}=\frac{n_{ijk}}{n_{test}}$$ は、π_ijk の無制限な最尤推定値です。

  • $${\widehat{\pi }}_{ijk}^{(3)}=\frac{n_{ijk}}{n_{test}+\lambda (c_{ki}-c_{kj})}$$ は、δ = 0 という帰無仮説における最尤推定値です。λ は、次の方程式の解です。

    $$\sum _{i,j,k}\frac{n_{ijk}(c_{ki}-c_{kj})}{n_{test}+\lambda (c_{ki}-c_{kj})}=0.$$

  • $$F_{{\chi }^2}(x;1)$$ は、x で評価した自由度 1 の χ² 累積分布関数です。

マクネマー検定

"マクネマー検定" は、標本のペアに依存関係があることによって生じる問題に対処して 2 つの母集団比率を比較する仮説検定です。

2 つの分類モデルの予測精度を比較する方法の 1 つは、次のとおりです。

1. データを学習セットとテスト セットに分割します。

2. 学習セットを使用して両方の分類モデルを学習させます。

3. テスト セットを使用してクラス ラベルを予測します。

4. 次の図のような 2 x 2 の表に結果を要約します。

   

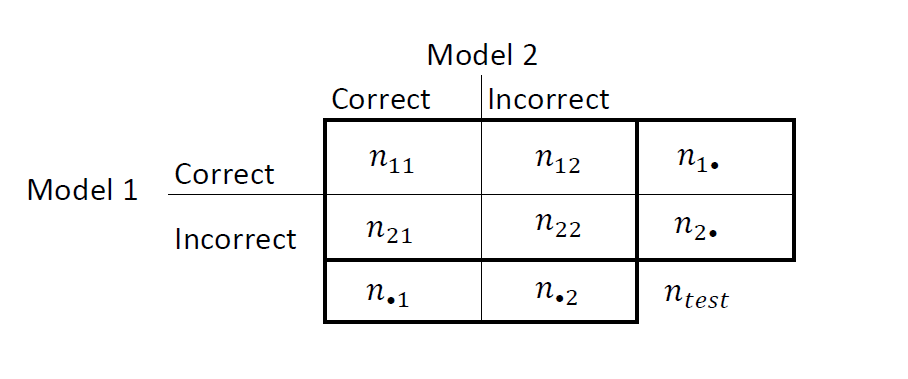
   n_ii は、一致するペアの数、つまり両方のモデルで同じように (正しくまたは誤って) 分類される観測の数です。i ≠ j の場合の n_ij は、一致しないペアの数、つまりモデルでさまざまに (正しくまたは誤って) 分類される観測の数です。

モデル 1 および 2 の誤分類率は、それぞれ $${\widehat{\pi }}_{2•}=n_{2•}/n$$ および $${\widehat{\pi }}_{•2}=n_{•2}/n$$ です。2 つのモデルの精度を比較する両側検定は、次のようになります。

$$\begin{array}{c}{H}_0:{\pi }_{•2}={\pi }_{2•}\\ H_1:{\pi }_{•2}\ne {\pi }_{2•}\end{array}.$$

この帰無仮説は母集団の周辺確率が同等であることを示しているので、帰無仮説は $$H_0:{\pi }_{12}={\pi }_{21}.$$ に縮小されます。また、この帰無仮説では、N₁₂ が (n₁₂ + n₂₁,0.5) の二項分布になります。[1]

以上は、マクネマー検定のバリエーションとして利用できる "漸近"、"厳密条件" および "mid-p 値" マクネマー検定の基礎となります。以下の定義は、利用可能なバリアントの概要です。

• 漸近 ― 漸近マクネマー検定の統計量と (有意水準 α に対する) 棄却域は、次のようになります。

  • 片側検定の場合、検定統計量は次のようになります。

    $$t_{a1}^{\ast }=\frac{n_{12}-n_{21}}{\sqrt{n_{12}+n_{21}}}.$$

    $$1-\Phi \left(\left|t_1^{\ast }\right|\right)<\alpha ,$$ である場合 (Φ は標準ガウス累積分布関数)、H₀ は棄却されます。

  • 両側検定の場合、検定統計量は次のようになります。

    $$t_{a2}^{\ast }=\frac{{\left(n_{12}-n_{21}\right)}^2}{n_{12}+n_{21}}.$$

    $$1-F_{{\chi }^2}\left(t_2^{\ast };m\right)<\alpha$$ である場合 ($$F_{{\chi }^2}(x;m)$$ は x で評価した χ_m² 累積分布関数)、H₀ は棄却されます。

  漸近検定では、大標本理論、具体的には二項分布に対するガウス近似が必要です。

  • 一致しないペアの総数 $$n_d=n_{12}+n_{21}$$ は、10 より大きくなければなりません ([1], Ch. 10.1.4)。

  • 一般に、漸近検定ではノミナルの被覆が保証されません。[2]のシミュレーション研究で示されているように、帰無仮説を誤って棄却する観測確率が α を超える可能性があります。しかし、統計的検出力に関しては漸近マクネマー検定は優れています。

• 厳密条件 — 厳密条件マクネマー検定の統計量と (有意水準 α に対する) 棄却域は、次のようになります ([4]、[5])。

  • 片側検定の場合、検定統計量は次のようになります。

    $$t_1^{\ast }=n_{12}.$$

    $$F_{\text{Bin}}\left(t_1^{\ast };n_d,0.5\right)<\alpha$$ である場合 ($$F_{\text{Bin}}\left(x;n,p\right)$$ は x で評価した、標本サイズが n、成功確率が p の二項累積分布関数)、H₀ は棄却されます。

  • 両側検定の場合、検定統計量は次のようになります。

    $$t_2^{\ast }=\min (n_{12},n_{21}).$$

    $$F_{\text{Bin}}\left(t_2^{\ast };n_d,0.5\right)<\alpha /2$$ である場合、H₀ は棄却されます。

  厳密条件検定では、常にノミナル カバレッジが達成されます。シミュレーション研究[2]によると、この検定は保守的であり、他のバリアントに比べて統計的検出力が不足しています。検定標本が小規模な場合や非常に離散的な場合は、mid-p 値検定の使用を検討してください ([1], Ch. 3.6.3)。

• mid-p 値検定 — mid-p 値マクネマー検定の統計量と (有意水準 α に対する) 棄却域は、次のようになります ([3])。

  • 片側検定の場合、検定統計量は次のようになります。

    $$t_1^{\ast }=n_{12}.$$

    $$F_{\text{Bin}}\left(t_1^{\ast }-1;n_{12}+n_{21},0.5\right)+0.5f_{\text{Bin}}\left(t_1^{\ast };n_{12}+n_{21},0.5\right)<\alpha$$ である場合 ($$F_{\text{Bin}}\left(x;n,p\right)$$ と $$f_{\text{Bin}}\left(x;n,p\right)$$ はそれぞれ x で評価した、標本サイズが n、成功確率が p の二項累積分布関数および二項確率密度関数)、H₀ は棄却されます。

  • 両側検定の場合、検定統計量は次のようになります。

    $$t_2^{\ast }=\min (n_{12},n_{21}).$$

    $$F_{\text{Bin}}\left(t_2^{\ast }-1;n_{12}+n_{21}-1,0.5\right)+0.5f_{\text{Bin}}\left(t_2^{\ast };n_{12}+n_{21},0.5\right)<\alpha /2$$ である場合、H₀ は棄却されます。

  mid-p 値検定は、厳密条件検定の過度に保守的な挙動に対処します。シミュレーション研究[2]によると、この検定はノミナルの被覆が達成され、統計的検出力が優れています。

分類損失

"分類損失" は、分類モデルまたは予測した一連のラベルの精度を示します。分類損失には、誤分類率と誤分類コストの 2 種類があります。

compareHoldout は、対立仮説における分類損失 (e1 および e2 参照) を返します (制限されない分類損失)。n_ijk はテスト標本観測値の個数であり、k は真のクラス、i は 1 番目の分類モデルによって割り当てられたラベル、j は 2 番目の分類モデルによって割り当てられたラベルです。対応する推定比率は $${\widehat{\pi }}_{ijk}=\frac{n_{ijk}}{n_{test}}.$$ です。テスト セットの標本サイズは $$\sum _{i,j,k}{n}_{ijk}=n_{test}.$$ です。インデックスは、1 から K (クラス数) までの値になります。

• "誤分類率" または分類誤差は、誤分類された観測値の比率を表す範囲 [0,1] のスカラー値です。つまり、1 番目の分類モデルの誤分類率は次のようになります。

  $$e_1={\displaystyle \sum _{j=1}^K{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{i\ne k}^{}{\widehat{\pi }}_{ijk}}}}.$$

  2 番目の分類モデルの誤分類率 (e₂) は、この式のインデックス i および j を入れ替えると得られます。

  分類精度は、誤分類率が 1 に近づくにつれて低下します。

• "誤分類コスト" は、指定されたコスト行列の値に対する相対的な分類品質の尺度となる、非負のスカラー値です。その解釈は、指定した誤分類のコストによって異なります。誤分類コストは、(コスト行列 C で指定される) 誤分類のコストの加重平均です。重みは、誤分類された各観測値の推定比率です。1 番目の分類モデルの誤分類コストは、次のようになります。

  $$e_1={\displaystyle \sum _{j=1}^K{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{i\ne k}^{}{\widehat{\pi }}_{ijk}{c}_{ki},}}}$$

  ここで c_kj は、真のクラスが k である場合に観測値をクラス j に分類するコストです。2 番目の分類モデルの誤分類コスト e₂ は、この式のインデックス i および j を入れ替えると得られます。

  一般に、コスト行列が一定の場合に誤分類コストが増加すると分類精度が低下します。

ヒント

• コストを考慮しない特徴選択を実行する方法の 1 つとして、次のようなものがあります。

  1. 完全な予測子セットを使用して、1 番目の分類モデル (C1) を学習させます。

  2. 縮小した予測子セットを使用して、2 番目の分類モデル (C2) を学習させます。

  3. 完全なテスト セットの予測子データを X1、縮小したテスト セットの予測子データを X2 に指定します。

  4. 「compareHoldout(C1,C2,X1,X2,Y,'Alternative','less')」と入力します。compareHoldout が 1 を返した場合、少ない予測子を使用する分類モデルは、完全な予測子セットを使用する分類モデルより性能が優れている十分な証拠を示しています。

  あるいは、2 つのモデルの精度に有意な差があるかどうかを評価することもできます。この評価を実行するには、手順 4 から 'Alternative','less' の指定を削除します。compareHoldout の実行により両側検定が実行され、h = 0 は、2 つのモデル間の精度の差を示す十分な証拠がないことを示します。

• コストを考慮する検定では数値を最適化しますが、これには追加の計算リソースが必要です。尤度比検定では、ある区間におけるラグランジュ乗数の根を求めるため間接的に数値を最適化します。データ セットによっては、根が区間の境界付近にある場合、メソッドが失敗する可能性があります。このため、Optimization Toolbox のライセンスがある場合は、コストを考慮するカイ二乗検定を代わりに実行することを検討してください。詳細については、CostTest およびコストを考慮する検定を参照してください。

代替機能

真のクラス ラベルのセットを予測するときに 2 つのクラス ラベルのセットについて精度を直接比較するには、testcholdout を使用します。

参照

[1] Agresti, A. Categorical Data Analysis, 2nd Ed. John Wiley & Sons, Inc.: Hoboken, NJ, 2002.

[2] Fagerlan, M.W., S. Lydersen, and P. Laake. “The McNemar Test for Binary Matched-Pairs Data: Mid-p and Asymptotic Are Better Than Exact Conditional.” BMC Medical Research Methodology. Vol. 13, 2013, pp. 1–8.

[3] Lancaster, H.O. “Significance Tests in Discrete Distributions.” JASA, Vol. 56, Number 294, 1961, pp. 223–234.

[4] McNemar, Q. “Note on the Sampling Error of the Difference Between Correlated Proportions or Percentages.” Psychometrika, Vol. 12, Number 2, 1947, pp. 153–157.

[5] Mosteller, F. “Some Statistical Problems in Measuring the Subjective Response to Drugs.” Biometrics, Vol. 8, Number 3, 1952, pp. 220–226.

拡張機能

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

使用上の注意事項および制限事項:

• この関数は、ClassificationNeuralNetwork モデルと CompactClassificationNeuralNetwork モデルの GPU 配列を完全にサポートします。

• この関数は、次の表に示す分類モデルの GPU 配列を制限付きでサポートします。

  完全またはコンパクトなモデル オブジェクト	制限
  ClassificationECOC または CompactClassificationECOC	バイナリ学習器は、タイプに応じて次の制限を受けます。 アンサンブル学習器には ClassificationEnsemble と同じ制限があります。 KNN 学習器には ClassificationKNN と同じ制限があります。 SVM 学習器には ClassificationSVM と同じ制限があります。 木学習器には ClassificationTree と同じ制限があります。
  ClassificationEnsemble または CompactClassificationEnsemble	弱学習器は、タイプに応じて次の制限を受けます。 KNN 学習器には ClassificationKNN と同じ制限があります。 木学習器には ClassificationTree と同じ制限があります。 判別学習器はサポートされません。
  ClassificationKNN	Kd 木最近傍探索法、関数ハンドル距離計量、fast 距離計量、または同順位使用を使って学習させたモデルはサポートされません。
  ClassificationSVM または CompactClassificationSVM	1 クラス分類はサポートされていません。
  ClassificationTree または CompactClassificationTree	代理分岐はサポートされません。

• compareHoldout は、次の場合にのみ GPU で実行されます。

  • 入力引数 X1 および X2 のいずれかまたは両方が GPU 配列である。

  • 入力引数 T1 および T2 のいずれかまたは両方に gpuArray 予測子変数が含まれている。

  • 入力引数 C1 および C2 のいずれかまたは両方に GPU 配列の入力引数が当てはめられている。

詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2015a で導入

R2024b: ニューラル ネットワーク モデルに対する GPU 配列の指定 (Parallel Computing Toolbox が必要)

compareHoldout は、ClassificationNeuralNetwork モデルと CompactClassificationNeuralNetwork モデルの GPU 配列を完全にサポートします。

参考

testckfold | testcholdout

トピック

• 仮説検定