fitcknn

k 最近傍分類器の学習

フィッシャーのアヤメのデータを使用して "k" 最近傍分類器に学習させます。ここで、予測子の最近傍の数 "k" は 5 です。

フィッシャーのアヤメのデータを読み込みます。

load fisheriris
X = meas;
Y = species;

X は、150 本のアヤメについて 4 つの測定値が含まれている数値行列です。Y は、対応するアヤメの種類が含まれている文字ベクトルの cell 配列です。

5 最近傍分類器を学習させます。非カテゴリカル予測子データを標準化します。

Mdl = fitcknn(X,Y,NumNeighbors=5,Standardize=true)

Mdl = 
  ClassificationKNN
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: {'setosa'  'versicolor'  'virginica'}
           ScoreTransform: 'none'
          NumObservations: 150
                 Distance: 'euclidean'
             NumNeighbors: 5


  Properties, Methods

Mdl は学習させた ClassificationKNN 分類器です。

ドット表記を使用して Mdl プロパティにアクセスします。

Mdl.ClassNames

ans = 3×1 cell
    {'setosa'    }
    {'versicolor'}
    {'virginica' }

Mdl.Prior

ans = 1×3

    0.3333    0.3333    0.3333

Mdl.Prior にはクラスの事前確率が格納されます。これは、fitcknn の名前と値の引数 Prior を使用して指定できます。クラス事前確率の順序は Mdl.ClassNames のクラスの順序に対応します。既定では、事前確率はデータ内のクラスのそれぞれの相対的頻度です。

学習後に事前確率をリセットすることもできます。たとえば、事前確率をそれぞれ 0.5、0.2 および 0.3 に設定します。

Mdl.Prior = [0.5 0.2 0.3];

Mdl を predict に渡すと、新しい測定値にラベルを付けることができます。また、crossvalに渡すと、分類器を交差検証できます。

ミンコフスキー計量を使用した "k" 最近傍分類器の学習

ミンコフスキー距離計量を使用して "k" 最近傍分類器に学習させます。

フィッシャーのアヤメのデータセットを読み込みます。

load fisheriris
X = meas;
Y = species;

3 最近傍分類器をミンコフスキー計量を使用して学習させます。ミンコフスキー計量を使用するには、網羅的探索を使用しなければなりません。非カテゴリカル予測子データを標準化します。

Mdl = fitcknn(X,Y,NumNeighbors=3, ...
    NSMethod="exhaustive",Distance="minkowski", ...
    Standardize=true);

Mdl は ClassificationKNN 分類器です。

Mdl の学習に使用されたミンコフスキー距離指数を調べます。

Mdl.DistParameter

ans = 
2

距離のパラメーターは ClassificationKNN オブジェクトの作成後に変更できます。たとえば、ミンコフスキー距離指数を 4 に設定します。

Mdl.DistParameter = 4;
Mdl.DistParameter

ans = 
4

カスタム距離計量を使用した k 最近傍分類器の学習

カイ二乗距離を使用して k 最近傍分類器に学習をさせます。

フィッシャーのアヤメのデータセットを読み込みます。

load fisheriris
X = meas;
Y = species;

j 次元の x 点と z 点のカイ二乗距離は次のようになります。

$χ (x, z) = \sqrt{\sum_{j = 1}^{J} w_{j} {(x_{j} - z_{j})}^{2}},$

ここで、 $w_{j}$ は次元 j に関連付けられている重みです。

カイ二乗距離関数を指定します。距離関数は以下の手順を実行しなければなりません。

X の 1 行 (たとえば x) および行列 Z を取る。
x を Z の各行と比較する。
長さ $n_{z}$ のベクトル D を返す。 $n_{z}$ は Z の行数です。D の各要素は x に対応する観測と Z の各行に対応する観測との間の距離です。

chiSqrDist = @(x,Z,wt)sqrt(((x-Z).^2)*wt);

この例では例示のために任意の重みを使用します。

3 最近傍分類器を学習させます。非カテゴリカル予測子データを標準化することをお勧めします。

k = 3;
w = [0.3; 0.3; 0.2; 0.2];
KNNMdl = fitcknn(X,Y,Distance=@(x,Z)chiSqrDist(x,Z,w), ...
    NumNeighbors=k,Standardize=true);

KNNMdl はClassificationKNN分類器です。

10 分割交差検証を使用して KNN 分類器を交差検証します。分類誤差を調べます。

rng(1); % For reproducibility
CVKNNMdl = crossval(KNNMdl);
classError = kfoldLoss(CVKNNMdl)

classError = 
0.0600

CVKNNMdl はClassificationPartitionedModel分類器です。

分類器を異なる加重スキームを使用するものと比較します。

w2 = [0.2; 0.2; 0.3; 0.3];
CVKNNMdl2 = fitcknn(X,Y,Distance=@(x,Z)chiSqrDist(x,Z,w2), ...
    NumNeighbors=k,KFold=10,Standardize=true);
classError2 = kfoldLoss(CVKNNMdl2)

classError2 = 
0.0400

2 番目の加重スキームから得られた分類器のほうが標本外パフォーマンスが優れています。

当てはめた KNN 分類器の最適化

fitcknn を使用して、"k" 最近傍分類器のハイパーパラメーターを自動的に最適化します。

fisheriris データセットを読み込みます。

load fisheriris
X = meas;
Y = species;

自動的なハイパーパラメーター最適化を使用して、5 分割交差検証損失を最小化するハイパーパラメーターを求めます。

再現性を得るために、乱数シードを設定し、"expected-improvement-plus" の獲得関数を使用します。

rng(1)
Mdl = fitcknn(X,Y,OptimizeHyperparameters="auto", ...
    HyperparameterOptimizationOptions= ...
    struct(AcquisitionFunctionName="expected-improvement-plus"))

|====================================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   | NumNeighbors |     Distance |  Standardize |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |              |
|====================================================================================================================|
|    1 | Best   |        0.04 |     0.46278 |        0.04 |        0.04 |           13 |    minkowski |         true |
|    2 | Accept |     0.19333 |     0.19938 |        0.04 |    0.046097 |            1 |  correlation |         true |
|    3 | Accept |    0.053333 |     0.06401 |        0.04 |    0.047573 |           14 |    chebychev |         true |
|    4 | Accept |    0.046667 |    0.076706 |        0.04 |    0.041053 |            2 |    minkowski |        false |
|    5 | Accept |    0.053333 |    0.054991 |        0.04 |    0.046782 |            7 |    minkowski |         true |
|    6 | Accept |     0.10667 |    0.095408 |        0.04 |    0.046422 |            2 |  mahalanobis |        false |
|    7 | Accept |    0.093333 |    0.042848 |        0.04 |    0.040581 |           75 |    minkowski |        false |
|    8 | Accept |     0.15333 |    0.039579 |        0.04 |    0.040008 |           75 |    minkowski |         true |
|    9 | Best   |        0.02 |    0.037067 |        0.02 |     0.02001 |            4 |    minkowski |        false |
|   10 | Accept |    0.026667 |    0.040269 |        0.02 |    0.020012 |            8 |    minkowski |        false |
|   11 | Accept |     0.21333 |    0.041647 |        0.02 |    0.020008 |           69 |    chebychev |         true |
|   12 | Accept |    0.053333 |    0.039976 |        0.02 |    0.020009 |            5 |    chebychev |         true |
|   13 | Accept |    0.053333 |    0.052008 |        0.02 |    0.020009 |            1 |    chebychev |         true |
|   14 | Accept |    0.053333 |    0.089704 |        0.02 |    0.020008 |            5 |   seuclidean |        false |
|   15 | Accept |    0.053333 |    0.053743 |        0.02 |    0.020008 |           21 |   seuclidean |        false |
|   16 | Accept |    0.053333 |    0.091401 |        0.02 |    0.020009 |            1 |   seuclidean |        false |
|   17 | Accept |     0.15333 |    0.063143 |        0.02 |    0.020007 |           75 |   seuclidean |        false |
|   18 | Accept |        0.02 |    0.059493 |        0.02 |    0.019969 |            5 |    minkowski |        false |
|   19 | Accept |     0.33333 |    0.073748 |        0.02 |    0.019898 |            2 |     spearman |        false |
|   20 | Accept |     0.23333 |    0.067935 |        0.02 |    0.019888 |           71 |  mahalanobis |        false |
|====================================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   | NumNeighbors |     Distance |  Standardize |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |              |
|====================================================================================================================|
|   21 | Accept |    0.046667 |    0.045476 |        0.02 |    0.019895 |            1 |    cityblock |         true |
|   22 | Accept |    0.053333 |    0.057295 |        0.02 |    0.019892 |            6 |    cityblock |         true |
|   23 | Accept |        0.12 |    0.057028 |        0.02 |    0.019895 |           75 |    cityblock |         true |
|   24 | Accept |        0.06 |     0.05025 |        0.02 |    0.019903 |            2 |    cityblock |        false |
|   25 | Accept |    0.033333 |    0.049075 |        0.02 |    0.019899 |           17 |    cityblock |        false |
|   26 | Accept |        0.12 |    0.054058 |        0.02 |    0.019907 |           74 |    cityblock |        false |
|   27 | Accept |    0.033333 |    0.045995 |        0.02 |    0.019894 |            7 |    cityblock |        false |
|   28 | Accept |        0.02 |    0.040869 |        0.02 |    0.019897 |            1 |    chebychev |        false |
|   29 | Accept |        0.02 |    0.096866 |        0.02 |    0.019891 |            4 |    chebychev |        false |
|   30 | Accept |        0.08 |    0.050688 |        0.02 |    0.019891 |           28 |    chebychev |        false |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 13.1433 seconds
Total objective function evaluation time: 2.2934

Best observed feasible point:
    NumNeighbors    Distance     Standardize
    ____________    _________    ___________

         4          minkowski       false   

Observed objective function value = 0.02
Estimated objective function value = 0.020124
Function evaluation time = 0.037067

Best estimated feasible point (according to models):
    NumNeighbors    Distance     Standardize
    ____________    _________    ___________

         5          minkowski       false   

Estimated objective function value = 0.019891
Estimated function evaluation time = 0.062602

Figure contains an axes object. The axes object with title Min objective vs. Number of function evaluations, xlabel Function evaluations, ylabel Min objective contains 2 objects of type line. These objects represent Min observed objective, Estimated min objective.

Mdl = 
  ClassificationKNN
                         ResponseName: 'Y'
                CategoricalPredictors: []
                           ClassNames: {'setosa'  'versicolor'  'virginica'}
                       ScoreTransform: 'none'
                      NumObservations: 150
    HyperparameterOptimizationResults: [1×1 BayesianOptimization]
                             Distance: 'minkowski'
                         NumNeighbors: 5


  Properties, Methods

学習させた分類器 Mdl は、最適な推定実行可能点に対応し、NumNeighbors、Distance、および Standardize に同じハイパーパラメーター値を使用しています。

結果を検証します。"k" 最近傍分類器で標準化を使用しない場合、ClassificationKNN オブジェクトの Mu プロパティと Sigma プロパティは空になることに注意してください。

bestEstimatedPoint = bestPoint(Mdl.HyperparameterOptimizationResults, ...
    Criterion="min-visited-upper-confidence-interval")

bestEstimatedPoint=1×3 table
    NumNeighbors    Distance     Standardize
    ____________    _________    ___________

         5          minkowski       false

classifierProperties = table(Mdl.NumNeighbors,string(Mdl.Distance), ...
    struct(Means=Mdl.Mu,StandardDeviations=Mdl.Sigma), ...
    VariableNames=["NumNeighbors","Distance","Standardize"])

classifierProperties=1×3 table
    NumNeighbors     Distance      Standardize
    ____________    ___________    ___________

         5          "minkowski"    1×1 struct

classifierProperties.Standardize

ans = struct with fields:
                 Means: []
    StandardDeviations: []

入力引数

`Tbl` — 標本データ
table

モデルを学習させるために使用する標本データ。table として指定します。Tbl の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。オプションとして、Tbl に応答変数用の列を 1 つ追加できます。文字ベクトルの cell 配列ではない cell 配列と複数列の変数は使用できません。

Tbl に応答変数が含まれている場合に Tbl 内の他の変数をすべて予測子として使用するには、ResponseVarName を使用して応答変数を指定します。
Tbl に応答変数が含まれている場合に Tbl 内の他の変数の一部のみを予測子として使用するには、formula を使用して式を指定します。
Tbl に応答変数が含まれていない場合は、Y を使用して応答変数を指定します。応答変数の長さと Tbl の行数は等しくなければなりません。

`ResponseVarName` — 応答変数名
`Tbl` 内の変数の名前

応答変数の名前。Tbl 内の変数の名前で指定します。

ResponseVarName には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、応答変数 Y が Tbl.Y として格納されている場合、"Y" として指定します。それ以外の場合、モデルを学習させるときに、Tbl の列は Y を含めてすべて予測子として扱われます。

応答変数は、categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列でなければなりません。Y が文字配列である場合、応答変数の各要素は配列の 1 つの行に対応しなければなりません。

名前と値の引数 ClassNames を使用してクラスの順序を指定することをお勧めします。

データ型: char | string

`formula` — 応答変数および予測子変数サブセットの説明モデル
文字ベクトル | string スカラー

応答変数および予測子変数サブセットの説明モデル。"Y~x1+x2+x3" という形式の文字ベクトルまたは string スカラーを指定します。この形式では、Y は応答変数を、x1、x2 および x3 は予測子変数を表します。

モデルに学習をさせるための予測子として Tbl 内の変数のサブセットを指定するには、式を使用します。式を指定した場合、formula に現れない Tbl 内の変数は使用されません。

式の変数名は Tbl の変数名 (Tbl.Properties.VariableNames) であり、有効な MATLAB^® 識別子でなければなりません。関数 isvarname を使用して Tbl の変数名を検証できます。変数名が有効でない場合、関数 matlab.lang.makeValidName を使用してそれらを変換できます。

データ型: char | string

`Y` — クラスラベル
categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

クラスラベル。categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列を指定します。Y の各行は、X の対応する行の分類を表します。

Y 内の NaN、'' (空の文字ベクトル)、"" (空の string)、<missing>、および <undefined> 値は欠損値と見なされます。このため、欠損応答がある観測値は学習に使用されません。

`X` — 予測子データ
数値行列

予測子データ。数値行列を指定します。

各行は 1 つの観測値 (インスタンスや例とも呼ばれます) に、各列は 1 つの予測子変数 (特徴量とも呼ばれます) に対応します。

Y の長さと X の行数は等しくなければなりません。

予測子の名前を X に表示される順序で指定するには、PredictorNames 名前と値のペアの引数を使用します。

データ型: double | single

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: fitcknn(Tbl,Y,NumNeighbors=3,NSMethod="exhaustive",Distance="minkowski") は最近傍探索法とミンコフスキー計量を使用して 3 最近傍の分類器を指定します。

メモ

交差検証の名前と値の引数は、名前と値の引数 OptimizeHyperparameters と一緒には使用できません。OptimizeHyperparameters の場合の交差検証は、名前と値の引数 HyperparameterOptimizationOptions を使用することのみによって変更できます。

モデルパラメーター

`BreakTies` — タイブレークアルゴリズム
`"smallest"` (既定値) | `"nearest"` | `"random"`

複数のクラスで最小コストが同じである場合に predict メソッドで使用されるタイブレークアルゴリズム。次のいずれかとして指定します。

"smallest" — 同順位グループの中で最小インデックスを使用します。
"nearest" — 同順位グループの中で最近傍のあるクラスを使用します。
"random" — 同順位グループの中でランダムなタイブレーカーを使用します。

既定では、同順位は k 最近傍の中で同じ数の最近傍点を複数のクラスがもつときに発生します。

例: BreakTies="nearest"

`BucketSize` — ノード内のデータ点の最大数
`50` (既定値) | 正の整数値

Kd 木の葉ノードにおけるデータ点の最大数。正の整数値として指定します。この引数は、NSMethod が "kdtree" の場合にのみ意味があります。

例: BucketSize=40

データ型: single | double

`CacheSize` — グラム行列に割り当てられるキャッシュのサイズ (メガバイト単位)
`1e3` (既定値) | `"maximal"` | 正のスカラー

R2025a 以降

グラム行列に割り当てられるキャッシュのサイズ (メガバイト単位)。"maximal" または正のスカラーとして指定します。CacheSize を使用できるのは、Distance の値が fast で始まる場合のみです。

CacheSize の値が "maximal" の場合、n 行 m 列のサイズのグラム行列に十分なメモリを割り当てるよう予測時に試行されます。ここで、n は学習予測子データ (X または Tbl) の行数、m はテスト予測子データの行数です。キャッシュサイズは、グラム行列に対して十分な大きさである必要はありませんが、少なくとも n 行 1 列のベクトルを保持する十分な大きさでなければなりません。そうでない場合、ユークリッド距離の計算に通常のアルゴリズムが使用されます。

Distance の値が fast で始まる場合に、CacheSize の値が大きすぎるか "maximal" であると、利用可能なメモリを超えるグラム行列の割り当てが試行されることがあります。この場合はエラーが発行されます。

例: CacheSize="maximal"

データ型: single | double | char | string

`CategoricalPredictors` — カテゴリカル予測子フラグ
`[]` | `"all"`

カテゴリカル予測子フラグ。次のいずれかを指定します。

"all" — すべての予測子がカテゴリカルです。
[] — カテゴリカル予測子はありません。

fitcknn の予測子データは、すべて連続、またはすべて categorical のいずれかでなければなりません。

予測子データが table (Tbl) 内にある場合、fitcknn は、その変数が logical ベクトル、categorical ベクトル、文字配列、string 配列または文字ベクトルの cell 配列のいずれかである場合に、変数を categorical であると見なします。Tbl に連続値とカテゴリカル値の両方が含まれている場合、fitcknn が、すべての予測子を、連続変数とカテゴリカル変数のどちらとして扱うか、その方法を判断できるよう、CategoricalPredictors の値を指定しなければなりません。
予測子データが行列 (X) である場合、fitcknn はすべての予測子が連続的であると見なします。X のすべての予測子を categorical として特定するには、CategoricalPredictors を "all" として指定します。

CategoricalPredictors を "all" に設定した場合、既定の設定の Distance は "hamming" です。

例: CategoricalPredictors="all"

`ClassNames` — 学習に使用するクラスの名前
categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

学習に使用するクラスの名前。categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列として指定します。ClassNames のデータ型は Tbl 内の応答変数または Y と同じでなければなりません。

ClassNames が文字配列の場合、各要素は配列の 1 つの行に対応しなければなりません。

ClassNames の使用目的は次のとおりです。

学習時のクラスの順序を指定する。
クラスの順序に対応する入力または出力引数の次元の順序を指定する。たとえば、Cost の次元の順序や predict によって返される分類スコアの列の順序を指定するために ClassNames を使用します。
学習用にクラスのサブセットを選択する。たとえば、Y に含まれているすべての異なるクラス名の集合が ["a","b","c"] であるとします。クラス "a" および "c" のみの観測値を使用してモデルに学習をさせるには、ClassNames=["a","c"] を指定します。

ClassNames の既定値は、Tbl 内の応答変数または Y に含まれているすべての異なるクラス名の集合です。

例: ClassNames=["b","g"]

`Cost` — 誤分類のコスト
正方行列 | 構造体

点の誤分類のコスト。次のいずれかとして指定します。

正方行列。Cost(i,j) は真のクラスが i である場合に点をクラス j に分類するコストです (行は真のクラス、列は予測したクラスに対応します)。Cost の対応する行および列についてクラスの順序を指定するには、名前と値のペアの引数 ClassNames をさらに指定します。
2 つのフィールドをもつ S を構成します。2 つのフィールドは、Y と同じ型のグループ名を表す変数が格納されている S.ClassNames と、コスト行列が格納されている S.ClassificationCosts です。

既定値は、i~=j の場合は Cost(i,j)=1、i=j の場合は Cost(i,j)=0 です。

データ型: single | double | struct

`Cov` — 共分散行列
`cov(X,"omitrows")` (既定値) | スカラー値の正定値行列

共分散行列。マハラノビス距離の計算時の共分散行列を表すスカラー値の正定値行列として指定します。この引数は、Distance が "mahalanobis" の場合にのみ有効です。

Standardize および Scale または Cov のいずれかを同時に指定できません。

データ型: single | double

`Distance` — 距離計量
`"cityblock"` | `"chebychev"` | `"correlation"` | `"cosine"` | `"euclidean"` | `"hamming"` | 関数ハンドル | ...

距離計量。有効な距離計量の名前または関数ハンドルとして指定します。使用できる距離計量名は、近傍探索法の選択 (NSMethod を参照) によって決まります。

`NSMethod` の値	距離計量名
`"exhaustive"`	`ExhaustiveSearcher` の任意の距離計量
`"kdtree"`	`"cityblock"`、`"chebychev"`、`"euclidean"`、または `"minkowski"`

この table には、ExhaustiveSearcher の有効な距離計量が含まれます。

距離計量名	説明
`"cityblock"`	市街地距離。
`"chebychev"`	チェビシェフ距離 (最大座標差)。
`"correlation"`	1 から、一連の値として扱われる観測間の標本線形相関係数を引きます。
`"cosine"`	1 から、ベクトルとして扱われる観測間の夾角の余弦を引きます。
`"euclidean"`	ユークリッド距離。
`"fasteuclidean"` (R2025a 以降)	予測子の数が 10 個以上の場合に時間の短縮になる代替アルゴリズムを使用して計算されるユークリッド距離。このアルゴリズムは高速ですが、場合によっては精度が低下することがあります。`fast` から始まるアルゴリズムでは、スパースデータはサポートされません。詳細については、高速ユークリッド距離アルゴリズムを参照してください。
`"fastseuclidean"` (R2025a 以降)	予測子の数が 10 個以上の場合に時間の短縮になる代替アルゴリズムを使用して計算される標準化されたユークリッド距離。このアルゴリズムは高速ですが、場合によっては精度が低下することがあります。`fast` から始まるアルゴリズムでは、スパースデータはサポートされません。詳細については、高速ユークリッド距離アルゴリズムを参照してください。
`"hamming"`	異なる座標のパーセンテージとなるハミング距離。
`"jaccard"`	1 から、ジャカード係数 (異なる非ゼロ座標の比率) を引いた値。
`"mahalanobis"`	正定値共分散行列 `C` を使用して計算される、マハラノビス距離。`C` の既定値は `X` の標本共分散行列であり、`cov(X,"omitrows")` によって計算されます。`C` に別の値を指定するには、名前と値の引数 `Cov` を使用します。
`"minkowski"`	ミンコフスキー距離。既定の指数は `2` です。別の指数を指定するには、名前と値の引数 `Exponent` を使用します。
`"seuclidean"`	標準化されたユークリッド距離。`X` と各クエリ点の間の各座標差分がスケーリングされます。つまり、スケール値 `S` で除算されます。`S` の既定値は `X` から計算される標準偏差で、`S = std(X,"omitnan")` です。`S` に別の値を指定するには、名前と値の引数 `Scale` を使用します。
`"spearman"`	1 から、観測値間の標本スピアマンの順位相関 (値の系列として扱われる) を引いた値。
`@distfun`	距離関数ハンドル。`distfun` は次の形式です function D2 = distfun(ZI,ZJ) % calculation of distance ... ここで `ZI` は 1 行の `X` または `Y` を含む `1` 行 `N` 列のベクトルです。 `ZJ` は複数行の `X` または `Y` を含む `M2` 行 `N` 列の行列です。 `D2` は `M2` 行 `1` 列の距離のベクトルであり、`D2(k)` は観測値 `ZI` と `ZJ(k,:)` の間の距離です。

CategoricalPredictors を "all" に指定した場合、既定の距離計量は "hamming" となります。それ以外の場合は、既定の距離計量は "euclidean" です。

詳細は、距離計量を参照してください。

例: Distance="minkowski"

データ型: char | string | function_handle

`DistanceWeight` — 距離重み付け関数
`"equal"` (既定値) | `"inverse"` | `"squaredinverse"` | 関数ハンドル

距離重み付け関数。関数ハンドルまたは次の表の値のいずれかとして指定します。

値	説明
`"equal"`	重み付けなし
`"inverse"`	重みは 1/距離です
`"squaredinverse"`	重みは 1/距離² です
`@fcn`	`fcn` は、非負の距離の行列を受け入れる関数であり、非負の距離重み付けを含む同じサイズの行列を返します。たとえば、`"squaredinverse"` は `@(d)d.^(-2)` と同じです。

例: DistanceWeight="inverse"

データ型: char | string | function_handle

`Exponent` — ミンコフスキー距離指数
`2` (既定値) | 正のスカラー値

ミンコフスキー距離指数。正のスカラー値として指定します。この引数は、Distance が "minkowski" の場合にのみ有効です。

例: Exponent=3

データ型: single | double

`IncludeTies` — 同順位使用フラグ
`false` (既定値) | `true`

同順位使用フラグ。距離の値が k 番目に小さい距離と等しい近傍点をすべて predict に含めるかどうかを示す logical 値として指定します。IncludeTies が true の場合、predict はすべての近傍点を含みます。それ以外の場合、predict は正確に k の近傍点を使用します。

例: IncludeTies=true

データ型: logical

`NSMethod` — 最近傍探索法
`"kdtree"` | `"exhaustive"`

最近傍探索法。"kdtree" または "exhaustive" を指定します。

"kdtree" — Kd 木を作成および使用して最近傍を探索します。"kdtree" は距離計量が次のいずれかである場合に有効です。
- "euclidean"
- "cityblock"
- "minkowski"
- "chebychev"
"exhaustive" — 網羅的探索アルゴリズムを使用します。新しい点 xnew のクラスを予測するときに、X 内のすべての点から xnew までの距離を計算して最近傍を探索します。

既定値は、X の列数が 10 以下で、X がスパースでないか gpuArray で、距離計量が "kdtree" 型の場合は "kdtree"、それ以外の場合は "exhaustive" です。

例: NSMethod="exhaustive"

`NumNeighbors` — 検出する最近傍の数
`1` (既定値) | 正の整数値

予測時に各点を分類するために検出する X の最近傍の数。正の整数値として指定します。

例: NumNeighbors=3

データ型: single | double

`PredictorNames` — 予測子変数名
一意な名前の string 配列 | 一意な文字ベクトルの cell 配列

予測子変数名。一意な名前の string 配列または一意な文字ベクトルの cell 配列として指定します。PredictorNames の機能は、学習データの提供方法によって決まります。

X と Y を指定した場合、PredictorNames を使用して X 内の予測子変数に名前を割り当てることができます。
- PredictorNames 内の名前の順序は、X の列の順序に一致しなければなりません。つまり、PredictorNames{1} は X(:,1) の名前、PredictorNames{2} は X(:,2) の名前であり、他も同様です。また、size(X,2) と numel(PredictorNames) は等しくなければなりません。
- 既定では PredictorNames は {'x1','x2',...} です。
Tbl を指定する場合、PredictorNames を使用して学習に使用する予測子変数を選択できます。つまり、fitcknn は、学習中に PredictorNames の予測子変数と応答変数のみを使用します。
- PredictorNames は Tbl.Properties.VariableNames のサブセットでなければならず、応答変数の名前を含めることはできません。
- 既定では、すべての予測子変数の名前が PredictorNames に格納されます。
- PredictorNames と formula の両方ではなく、いずれか一方を使用して学習用の予測子を指定することをお勧めします。

例: "PredictorNames",["SepalLength","SepalWidth","PetalLength","PetalWidth"]

データ型: string | cell

`Prior` — 事前確率
`"empirical"` (既定値) | `"uniform"` | スカラー値のベクトル | 構造体

各クラスの事前確率。次の表の値として指定します。

値	説明
`"empirical"`	クラスの事前確率は、`Y` のクラスの相対的頻度です。
`"uniform"`	クラスの事前確率はいずれも 1/K (K はクラス数) となります。
数値ベクトル	各要素はクラスの事前確率です。`Mdl.ClassNames` に従って要素を並べ替えるか、`ClassNames` 名前と値のペアの引数を使用して順序を指定します。要素は合計が `1` になるように正規化されます。
構造体	構造体 `S` には 2 つのフィールドがあります。 `S.ClassNames`: `Y` と同じ型の変数のクラス名が格納されます。 `S.ClassProbs`: 対応する事前確率のベクトルが格納されます。要素は合計が `1` になるように正規化されます。

Weights と Prior の両方に値を設定した場合は、重みは合計が対応するクラスの事前確率の値になるように再正規化されます。

例: Prior="uniform"

データ型: char | string | single | double | struct

`ResponseName` — 応答変数名
`"Y"` (既定値) | 文字ベクトル | string スカラー

応答変数名。文字ベクトルまたは string スカラーとして指定します。

Y を指定した場合、ResponseName を使用して応答変数の名前を指定できます。
ResponseVarName または formula を指定した場合、ResponseName を使用できません。

例: ResponseName="response"

データ型: char | string

`Scale` — 距離スケール
`std(X,"omitnan")` (既定値) | 非負のスカラー値のベクトル

距離スケール。X の列数と同じ長さの非負のスカラー値を含むベクトルとして指定します。X とクエリ点の間の各座標差分は、Scale の対応する要素でスケーリングされます。この引数は、Distance が "seuclidean" の場合にのみ有効です。

Standardize および Scale または Cov のいずれかを同時に指定できません。

データ型: single | double

`ScoreTransform` — スコア変換
`"none"` (既定値) | `"doublelogit"` | `"invlogit"` | `"ismax"` | `"logit"` | 関数ハンドル | ...

スコア変換。文字ベクトル、string スカラー、または関数ハンドルとして指定します。

次の表は、使用可能な文字ベクトルおよび string スカラーをまとめています。

値	説明
`"doublelogit"`	1/(1 + e^–2x)
`"invlogit"`	log(x / (1 – x))
`"ismax"`	最大のスコアをもつクラスのスコアを 1 に設定し、他のすべてのクラスのスコアを 0 に設定する
`"logit"`	1/(1 + e^–x)
`"none"` または `"identity"`	x (変換なし)
`"sign"`	x < 0 のとき –1 x = 0 のとき 0 x > 0 のとき 1
`"symmetric"`	2x – 1
`"symmetricismax"`	最大のスコアをもつクラスのスコアを 1 に設定し、他のすべてのクラスのスコアを –1 に設定する
`"symmetriclogit"`	2/(1 + e^–x) – 1

MATLAB 関数またはユーザー定義関数の場合は、スコア変換用の関数ハンドルを使用します。関数ハンドルは、行列 (元のスコア) を受け入れて同じサイズの行列 (変換したスコア) を返さなければなりません。

例: ScoreTransform="logit"

データ型: char | string | function_handle

`Standardize` — 予測子を標準化するためのフラグ
`false` (既定値) | `true`

予測子を標準化するフラグ。true (1) または false (0) として指定します。

Standardize=true を設定すると、予測子データの各列 (X) がそれぞれ列の平均と標準偏差でセンタリングおよびスケーリングされます。

すべての予測子がカテゴリカルの場合、カテゴリカル予測子は標準化されずエラーがスローされます。

Standardize=true および Scale または Cov のいずれかを同時に指定できません。

予測子データの標準化をお勧めします。

例: Standardize=true

データ型: logical

`Weights` — 観測値の重み
正の値の数値ベクトル | `Tbl` 内の変数の名前

観測値の重み。正の値の数値ベクトルまたは Tbl 内の変数の名前として指定します。X または Tbl の各行に含まれている観測値は、Weights の対応する値で重み付けされます。Weights のサイズは、X または Tbl の行数と等しくなければなりません。

入力データを table Tbl として指定した場合、Weights は数値ベクトルが含まれている Tbl 内の変数の名前にすることができます。この場合、Weights には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、重みベクトル W が Tbl.W として格納されている場合、"W" として指定します。それ以外の場合、モデルに学習をさせるときに、Tbl の列は W を含めてすべて予測子または応答として扱われます。

既定の設定では、Weights は ones(n,1) です。n は X または Tbl の観測値数です。

合計が各クラスの事前確率の値と等しくなるように Weights が正規化されます。Inf の重みはサポートされません。

データ型: double | single | char | string

交差検証オプション

`CrossVal` — 交差検証フラグ
`"off"` (既定値) | `"on"`

交差検証のフラグ。"on" または "off" として指定します。

"on" を指定した場合、10 分割の交差検証が実施されます。

この交差検証の設定をオーバーライドするには、名前と値の引数 CVPartition、Holdout、KFold、Leaveout のいずれかを使用します。交差検証済みモデルを作成するために一度に使用できる交差検証の名前と値の引数は 1 つだけです。

または、crossval メソッドを使用して、後で Mdl に交差検証を実施します。

例: Crossval="on"

`CVPartition` — 交差検証分割
`[]` (既定値) | `cvpartition` オブジェクト

交差検証分割。交差検証のタイプと学習セットおよび検証セットのインデックス付けを指定する cvpartition オブジェクトとして指定します。

交差検証済みモデルの作成で指定できる名前と値の引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: cvp = cvpartition(500,KFold=5) を使用して、500 個の観測値に対する 5 分割交差検証について無作為な分割を作成するとします。この場合、CVPartition=cvp を設定して交差検証分割を指定できます。

`Holdout` — ホールドアウト検証の対象データの比率
(0,1) の範囲のスカラー値

ホールドアウト検証に使用するデータの比率。範囲 (0,1) のスカラー値として指定します。Holdout=p を指定した場合、以下の手順が実行されます。

p*100% のデータを無作為に選択して検証データとして確保し、残りのデータを使用してモデルに学習をさせる。
コンパクトな学習済みモデルを交差検証済みモデルの Trained プロパティに格納する。

交差検証済みモデルの作成で指定できる名前と値の引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: Holdout=0.1

データ型: double | single

`KFold` — 分割の数
`10` (既定値) | 1 より大きい正の整数値

交差検証済みモデルで使用する分割の数。1 より大きい正の整数値として指定します。KFold=k を指定した場合、以下の手順が実行されます。

データを無作為に k 個のセットに分割する。
各セットについて、そのセットを検証データとして確保し、他の k – 1 個のセットを使用してモデルに学習をさせる。
k 個のコンパクトな学習済みモデルを、交差検証済みモデルの Trained プロパティに含まれている k 行 1 列の cell ベクトルに格納する。

交差検証済みモデルの作成で指定できる名前と値の引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: KFold=5

データ型: single | double

`Leaveout` — Leave-one-out 法の交差検証のフラグ
`"off"` (既定値) | `"on"`

Leave-one-out 法の交差検証のフラグ。"on" または "off" として指定します。Leaveout="on" を指定した場合、n 個の観測値 (n は、モデルの NumObservations プロパティで指定される、欠損観測値を除外した観測値の個数) のそれぞれについて以下の手順が実行されます。

いずれかの観測値を検証データとして確保し、他の n - 1 個の観測値を使用してモデルに学習をさせる。
n 個のコンパクトな学習済みモデルを、交差検証済みモデルの Trained プロパティに含まれている n 行 1 列の cell ベクトルに格納する。

交差検証済みモデルの作成で指定できる名前と値の引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: Leaveout="on"

データ型: char | string

ハイパーパラメーター最適化オプション

`OptimizeHyperparameters` — 最適化するパラメーター
`"none"` (既定値) | `"auto"` | `"all"` | 使用可能パラメーター名の string 配列または cell 配列 | `optimizableVariable` オブジェクトのベクトル

最適化するパラメーター。次のいずれかを指定します。

"none" — 最適化を行いません。
"auto" — ["Distance","NumNeighbors","Standardize"] を使用します。
"all" — すべての使用可能パラメーターを最適化します。
使用可能パラメーター名の string 配列または cell 配列。
optimizableVariable オブジェクトのベクトル。通常は hyperparameters の出力です。

最適化では、パラメーターを変化させることにより、fitcknn の交差検証損失 (誤差) を最小化しようとします。交差検証のタイプおよびその他の最適化の側面を制御するには、名前と値の引数 HyperparameterOptimizationOptions を使用します。HyperparameterOptimizationOptions を使用すると、ConstraintType オプションと ConstraintBounds オプションを設定することにより、交差検証損失の代わりに (コンパクトな) モデルサイズを最適化の目的として使用できます。

メモ

OptimizeHyperparameters の値は、他の名前と値の引数を使用して指定した値より優先されます。たとえば、OptimizeHyperparameters を "auto" に設定すると、fitcknn は "auto" オプションに対応するハイパーパラメーターを最適化して、ハイパーパラメーターに指定された値を無視します。

fitcknn では、以下のパラメーターを使用できます。

Distance — fitcknn は、"cityblock"、"chebychev"、"correlation"、"cosine"、"euclidean"、"hamming"、"jaccard"、"mahalanobis"、"minkowski"、"seuclidean" および "spearman" で探索します。
DistanceWeight — fitcknn は、"equal"、"inverse" および "squaredinverse" で探索します。
Exponent — fitcknn は、既定では範囲 [0.5,3] で、正の実数値を探索します。
NumNeighbors — fitcknn は、既定では範囲 [1,max(2,round(NumObservations/2))] の対数スケールで、正の整数値を探索します。
Standardize — fitcknn は、値 "true" および "false" で探索します。

既定以外のパラメーターを設定するには、既定以外の値が含まれている optimizableVariable オブジェクトのベクトルを渡します。以下に例を示します。

load fisheriris
params = hyperparameters("fitcknn",meas,species);
params(1).Range = [1,20];

OptimizeHyperparameters の値として params を渡します。

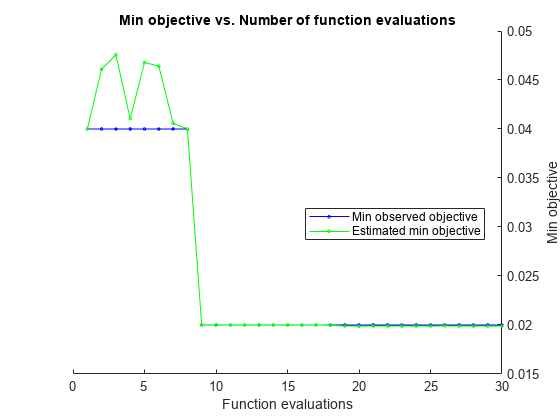
既定では、コマンドラインに反復表示が表示され、最適化のハイパーパラメーターの個数に従ってプロットが表示されます。最適化とプロットにおける目的関数は誤分類率です。反復表示を制御するには、名前と値の引数 HyperparameterOptimizationOptions の Verbose オプションを設定します。プロットを制御するには、名前と値の引数 HyperparameterOptimizationOptions の ShowPlots フィールドを設定します。

たとえば、当てはめた KNN 分類器の最適化を参照してください。

例: OptimizeHyperparameters="auto"

`HyperparameterOptimizationOptions` — 最適化のオプション
`HyperparameterOptimizationOptions` オブジェクト | 構造体

最適化のオプション。HyperparameterOptimizationOptions オブジェクトまたは構造体として指定します。この引数を指定すると、名前と値の引数 OptimizeHyperparameters の効果が変化します。HyperparameterOptimizationOptions を指定する場合、OptimizeHyperparameters も指定しなければなりません。オプションはいずれも任意です。ただし、AggregateOptimizationResults を返すには ConstraintBounds と ConstraintType を設定しなければなりません。構造体で設定できるオプションは HyperparameterOptimizationOptions オブジェクトと同じです。

オプション	値	既定の設定
`Optimizer`	`"bayesopt"` — ベイズ最適化を使用。内部的には `bayesopt` が呼び出されます。 `"gridsearch"` — 次元ごとに `NumGridDivisions` の値があるグリッド探索を使用。`"gridsearch"` では、グリッドからの一様な非復元抽出により、無作為な順序で探索します。最適化後、`sortrows(Mdl.HyperparameterOptimizationResults)` コマンドを使用してグリッド順の table を取得できます。 `"randomsearch"` — `MaxObjectiveEvaluations` 個の点で無作為に探索。	`"bayesopt"`
`ConstraintBounds`	N 個の最適化問題の制約範囲。N 行 2 列の数値行列または `[]` として指定します。`ConstraintBounds` の列には最適化問題の下限と上限の値が含まれます。`ConstraintBounds` を数値ベクトルとして指定すると、`ConstraintBounds` の 2 列目に値が代入され、1 列目にはゼロが代入されます。`ConstraintBounds` を指定する場合、`ConstraintType` も指定しなければなりません。	`[]`
`ConstraintTarget`	最適化問題の制約ターゲット。`"matlab"` または `"coder"` として指定します。`ConstraintBounds` と `ConstraintType` が `[]` の場合に `ConstraintTarget` を設定すると、`ConstraintTarget` は `[]` に設定されます。`ConstraintTarget` と `ConstraintType` の値により、目的関数と制約関数が決まります。詳細については、`HyperparameterOptimizationOptions` を参照してください。	`ConstraintBounds` と `ConstraintType` を指定する場合の既定値は `"matlab"` です。そうでない場合、既定値は `[]` となります。
`ConstraintType`	最適化問題の制約タイプ。`"size"` または `"loss"` として指定します。`ConstraintType` を指定する場合、`ConstraintBounds` も指定しなければなりません。`ConstraintTarget` と `ConstraintType` の値により、目的関数と制約関数が決まります。詳細については、`HyperparameterOptimizationOptions` を参照してください。	`[]`
`AcquisitionFunctionName`	獲得関数のタイプ: `"expected-improvement-per-second-plus"` `"expected-improvement"` `"expected-improvement-plus"` `"expected-improvement-per-second"` `"lower-confidence-bound"` `"probability-of-improvement"` 目的関数の実行時に最適化が決まるので、名前に `per-second` が含まれている獲得関数は、再現性がある結果を生成しません。名前に `plus` が含まれている獲得関数は、領域を過剰利用している場合に動作を変更します。詳細は、獲得関数のタイプを参照してください。	`"expected-improvement-per-second-plus"`
`MaxObjectiveEvaluations`	目的関数評価の最大数。`ConstraintBounds` を使用して最適化問題を複数指定する場合、`MaxObjectiveEvaluations` の値は各最適化問題に個別に適用されます。	`"bayesopt"` および `"randomsearch"` の場合は `30`、`"gridsearch"` の場合はグリッド全体
`MaxTime`	最適化の制限時間。非負の実数スカラーとして指定します。制限時間の単位は、`tic` と `toc` によって測定される秒です。`MaxTime` の値にかかわらず、少なくとも 1 回は最適化反復が実行されます。`MaxTime` は関数評価を中断させないため、実行時間が `MaxTime` を超える可能性があります。`ConstraintBounds` を使用して最適化問題を複数指定する場合、制限時間は各最適化問題に個別に適用されます。	`Inf`
`NumGridDivisions`	`Optimizer="gridsearch"` における各次元の値の個数。値は、各次元の値の個数を表す正の整数のベクトル、またはすべての次元に適用されるスカラーが可能です。カテゴリカル変数の場合、このオプションは無視されます。	`10`
`ShowPlots`	最適化の進行状況のプロットを表示するかどうかを示す logical 値。このオプションが `true` の場合、最適な観測された目的関数値が反復回数に対してプロットされます。ベイズ最適化を使用する場合 (`Optimizer="bayesopt"`)、最適な推定された目的関数値もプロットされます。最適な観測された目的関数値および最適な推定された目的関数値は、反復表示の `BestSoFar (observed)` 列および `BestSoFar (estim.)` 列の値にそれぞれ対応しています。これらの値は、`Mdl.HyperparameterOptimizationResults` のプロパティ `ObjectiveMinimumTrace` および `EstimatedObjectiveMinimumTrace` で確認できます。問題にベイズ最適化の最適化パラメーターが 1 つまたは 2 つある場合、`ShowPlots` はパラメーターに対する目的関数のモデルもプロットします。	`true`
`SaveIntermediateResults`	最適化の結果を保存するかどうかを示す logical 値。このオプションが `true` の場合、`"BayesoptResults"` という名前のワークスペース変数が反復ごとに上書きされます。この変数は `BayesianOptimization` オブジェクトです。`ConstraintBounds` を使用して最適化問題を複数指定する場合、ワークスペース変数は `"AggregateBayesoptResults"` という名前の `AggregateBayesianOptimization` オブジェクトになります。	`false`
`Verbose`	コマンドラインにおける表示レベル: `0` — 反復表示なし `1` — 反復表示あり `2` — 反復表示と追加情報詳細については、`bayesopt` の名前と値の引数 `Verbose` およびベイズ最適化の使用による分類器の当てはめの最適化の例を参照してください。	`1`
`UseParallel`	ベイズ最適化を並列実行するかどうかを示す logical 値。並列実行には Parallel Computing Toolbox™ が必要です。並列でのタイミングに再現性がないため、並列ベイズ最適化で再現性のある結果が生成されるとは限りません。詳細については、並列ベイズ最適化を参照してください。	`false`
`Repartition`	反復ごとに交差検証を再分割するかどうかを示す論理値。このオプションが `false` の場合、オプティマイザーは単一の分割を最適化に使用します。分割ノイズが考慮されるので、通常は値を `true` にすると最も確実な結果が得られます。ただし、`true` で最適な結果を得るには、2 倍以上の関数評価が必要になります。	`false`
次の 3 つのオプションのいずれか 1 つのみを指定してください。
`CVPartition`	`cvpartition` によって作成された `cvpartition` オブジェクト	交差検証オプションが指定されていない場合は `KFold=5`
`Holdout`	ホールドアウトの比率を表す範囲 `(0,1)` のスカラー
`KFold`	1 より大きい整数

例: HyperparameterOptimizationOptions=struct(UseParallel=true)

出力引数

`Mdl` — 学習済みの k 最近傍分類モデル
`ClassificationKNN` モデルオブジェクト | `ClassificationPartitionedModel` 交差検証済みモデルオブジェクト

学習済みの k 最近傍分類モデル。ClassificationKNN モデルオブジェクトまたは ClassificationPartitionedModel 交差検証済みモデルオブジェクトとして返されます。

名前と値のペアの引数 KFold、Holdout、CrossVal、CVPartition のいずれかを設定した場合、Mdl は ClassificationPartitionedModel 交差検証済みモデルオブジェクトになります。それ以外の場合、Mdl は ClassificationKNN モデルオブジェクトになります。

Mdl のプロパティを参照するには、ドット表記を使用します。たとえば、コマンドウィンドウで距離計量を表示するには、Mdl.Distance を入力します。

OptimizeHyperparameters を指定して HyperparameterOptimizationOptions の ConstraintType オプションと ConstraintBounds オプションを設定している場合、Mdl はモデルオブジェクトの N 行 1 列の cell 配列になります。ここで、N は ConstraintBounds の行数と等しくなります。いずれの最適化問題からも実行可能なモデルが得られない場合、cell 配列の各値が [] になります。

`AggregateOptimizationResults` — 最適化の結果の集計
`AggregateBayesianOptimization` オブジェクト

複数の最適化問題についての最適化の結果の集計。AggregateBayesianOptimization オブジェクトとして返されます。AggregateOptimizationResults を返すには、OptimizeHyperparameters と HyperparameterOptimizationOptions を指定しなければなりません。HyperparameterOptimizationOptions の ConstraintType オプションと ConstraintBounds オプションも指定する必要があります。この出力の生成方法を示す例については、Hyperparameter Optimization with Multiple Constraint Boundsを参照してください。

ヒント

モデルに学習をさせた後で、新しいデータについてラベルを予測する C/C++ コードを生成できます。C/C++ コードの生成には MATLAB Coder™ が必要です。詳細については、コード生成の紹介を参照してください。

アルゴリズム

欠損観測値

NaNs または <undefined> は観測値の欠損を示します。以下はデータセットまたは重みに欠損した観測がある場合の fitcknn の動作の説明です。

Y の任意の値または重みに欠損がある場合、fitcknn はこれらの値を Y から削除し、重みおよび対応する X の行をデータから削除します。重みは再度正規化され、合計は 1 になります。
予測子を標準化する (Standardize=true)、またはスケーリングなしの標準化されたユークリッド距離を指定する (Distance="seuclidean") 場合、fitcknn は平均と標準偏差を計算する前に、欠損した観測値を各予測子から削除します。つまり、ソフトウェアは、mean および std を各予測子で "omitnan" オプションを使用して実装します。
共分散行列を使用せずにマハラノビス距離 (Distance="mahalanobis") を指定する場合、fitcknn によって少なくとも 1 つの欠損値を含む X の行が削除されます。つまり、ソフトウェアは、cov を予測子行列 X で "omitrows" オプションを使用して実装します。

誤分類コスト、事前確率、および観測値の重み

名前と値の引数 Cost、Prior、および Weights を指定すると、出力モデルオブジェクトに Cost、Prior、および W の各プロパティの指定値がそれぞれ格納されます。Cost プロパティには、ユーザー指定のコスト行列がそのまま格納されます。Prior プロパティと W プロパティには、正規化後の事前確率と観測値の重みがそれぞれ格納されます。詳細については、誤分類コスト行列、事前確率、および観測値の重みを参照してください。
Cost プロパティは予測に使用されますが、学習には使用されません。したがって、Cost は読み取り専用ではなく、学習済みモデルの作成後にドット表記を使用してプロパティの値を変更できます。
Standardize=true を設定すると仮定します。
- 名前と値の引数 Prior または Weights も指定した場合、fitcknn は対応する加重平均および加重標準偏差を使用して予測子を標準化します。具体的には、fitcknn は予測子 j の標準化のために次を使用します。
  - $x_{j}^{*} = \frac{x_{j} - μ_{j}^{*}}{σ_{j}^{*}} .$
    $μ_{j}^{*} = \frac{1}{\sum_{k} w_{k}} \sum_{k} w_{k} x_{j k} .$
    x_jk は、予測子 j (列) の観測値 k (行) です。
    ${(σ_{j}^{*})}^{2} = \frac{\sum_{k} w_{k}}{{(\sum_{k} w_{k})}^{2} - \sum_{k} w_{k}^{2}} \sum_{k} w_{k} {(x_{j k} - μ_{j}^{*})}^{2} .$
- Distance="mahalanobis" または Distance="seuclidean" も設定する場合、Scale または Cov は指定できません。代わりに、次の処理が実行されます。
  1. 各予測子の平均と標準偏差を計算する。
  2. ステップ 1 の結果を使用してデータを標準化する。
  3. distance パラメーターの値をそれぞれの既定値を使用して計算する。
Scale および Prior または Weights のいずれかを指定する場合、観測された距離は加重標準偏差でスケーリングされます。
Cov および Prior または Weights のいずれかを指定する場合、加重共分散行列が距離に適用されます。つまり、次のようになります。

$C o v = \frac{\sum_{k} w_{k}}{{(\sum_{k} w_{k})}^{2} - \sum_{k} w_{k}^{2}} \sum_{j} \sum_{k}^{} w_{k} {(x_{j k} - μ_{j}^{*})}^{'} (x_{j} - μ_{j}^{*}) .$

高速ユークリッド距離アルゴリズム

Distance 引数の fast から始まる値 ("fasteuclidean" や "fastseuclidean" など) で使用されるアルゴリズムでは、計算時間の短縮のために追加のメモリを使用してユークリッド距離が計算されます。このアルゴリズムは、Albanie の[1]などで "ユークリッド距離行列トリック" として提唱されているものです。内部テストでは、このアルゴリズムによって予測子の数が 10 個以上の場合に時間の短縮になることが確認されています。fast から始まるアルゴリズムでは、スパースデータはサポートされません。

このアルゴリズムでは、x_i と x_j のすべての点間の距離の行列 D を求めるために (x_i のそれぞれに n 個の変数を格納)、次の方程式の最後の行を使用して距離を計算します。

$\begin{matrix} D_{i, j}^{2} = ‖ x_{i} - x_{j} ‖^{2} \\ = (^{x_{i} - x_{j}) T} (x_{i} - x_{j}) \\ = ‖ x_{i} ‖^{2} - 2 x_{i}^{T} x_{j} + ‖ x_{j} ‖^{2} . \end{matrix}$

方程式の最後の行にある行列 $x_{i}^{T} x_{j}$ は "グラム行列" と呼ばれます。正方化と加算によって平方距離を計算する代わりに、グラム行列を計算して使用すると、一連の平方距離の計算は高速になりますが、数値的安定性は少し低くなります。詳細については、Albanie [1]を参照してください。

グラム行列を格納するためにソフトウェアで既定で使用されるキャッシュのサイズは 1e3 メガバイトです。キャッシュサイズは名前と値の引数 CacheSize を使用して設定できます。CacheSize の値が大きすぎるか "maximal" である場合、利用可能なメモリを超えるグラム行列の割り当てが試行されることがあります。この場合はエラーが発行されます。

参照

[1] Albanie, Samuel. Euclidean Distance Matrix Trick. June, 2019. Available at https://samuelalbanie.com/files/Euclidean_distance_trick.pdf.

予測

ClassificationKNN は次と同等の手順を使用して点 xnew の分類を予測します。

xnew に最近傍である学習セット X の NumNeighbors 点を検出します。
それらの最近傍点への NumNeighbors 応答値 Y を検出します。
Y の値の中で事後確率が最も大きい ynew 分類ラベルを割り当てます。

詳細は、『predict』ドキュメンテーションの事後確率を参照してください。

代替方法

fitcknn はマルチクラス KNN 分類器を学習させることができます。また、fitcecoc を使用して、マルチクラス学習問題を一連の KNN バイナリ学習器に縮小できます。

拡張機能

自動並列サポート
Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

ハイパーパラメーターの最適化を並列実行するには、fitcknn 関数を呼び出すときに名前と値の引数 HyperparameterOptimizationOptions で UseParallel=true オプションを使用します。

並列的なハイパーパラメーターの最適化の詳細については、並列ベイズ最適化を参照してください。

並列計算の全般的な情報については、自動並列サポートを使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

使用上の注意および制限:

既定では、fitcknn は、gpuArray の入力引数に対して網羅的最近傍探索アルゴリズムを使用します。
名前と値の引数 NSMethod を "kdtree" として指定することはできません。
名前と値の引数 Distance を "fasteuclidean"、"fastseuclidean"、または関数ハンドルとして指定することはできません。
名前と値の引数 IncludeTies を true として指定することはできません。
fitcknn は、次のいずれかに該当する場合に GPU でモデルを当てはめます。
- 入力引数 X が gpuArray オブジェクトである。
- 入力引数 Tbl に gpuArray 予測子変数が含まれている。

詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2014a で導入