このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

bayesopt

ベイズ最適化を使用した最適な機械学習のハイパーパラメーターの選択

構文

results = bayesopt(fun,vars)

results = bayesopt(fun,vars,Name,Value)

説明

results = bayesopt(fun,vars) は、fun(vars) を最小化する vars の値を求めようとします。

メモ

目的関数に追加のパラメーターを含めるには、関数のパラメーター化を参照してください。

results = bayesopt(fun,vars,Name,Value) は、引数 Name,Value に従って最適化プロセスを修正します。

例

bayesopt の使用による BayesianOptimization オブジェクトの作成

この例では、bayesopt を使用して交差検証損失を最小化することにより BayesianOptimization オブジェクトを作成する方法を示します。

ionosphere データに対し、KNN 分類器のハイパーパラメーターを最適化、つまり、交差検証損失が最小になる KNN のハイパーパラメーターを求めます。bayesopt で次のハイパーパラメーターに対する最小化を行います。

• 1 ～ 30 の最近傍サイズ。

• 距離関数 'chebychev'、'euclidean' および 'minkowski'

再現性を得るため、乱数シードと分割を設定し、AcquisitionFunctionName オプションを 'expected-improvement-plus' に設定します。反復表示を非表示にするには 'Verbose' を 0 に設定します。このデータを組み込む無名関数として fun を作成して、区分 c と近似データ X および Y を目的関数 fun に渡します。関数のパラメーター化 を参照してください。

load ionosphere
rng default
num = optimizableVariable('n',[1,30],'Type','integer');
dst = optimizableVariable('dst',{'chebychev','euclidean','minkowski'},'Type','categorical');
c = cvpartition(351,'Kfold',5);
fun = @(x)kfoldLoss(fitcknn(X,Y,'CVPartition',c,'NumNeighbors',x.n,...
    'Distance',char(x.dst),'NSMethod','exhaustive'));
results = bayesopt(fun,[num,dst],'Verbose',0,...
    'AcquisitionFunctionName','expected-improvement-plus')

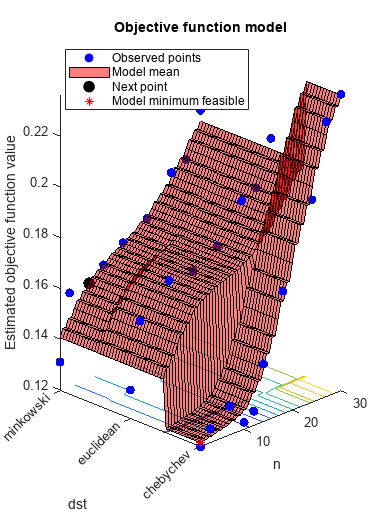
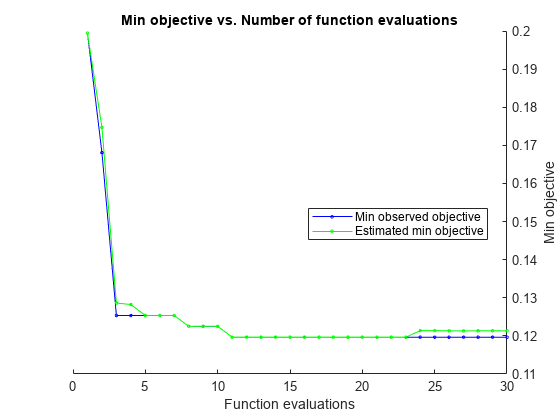
results = 
  BayesianOptimization with properties:

                      ObjectiveFcn: @(x)kfoldLoss(fitcknn(X,Y,'CVPartition',c,'NumNeighbors',x.n,'Distance',char(x.dst),'NSMethod','exhaustive'))
              VariableDescriptions: [1x2 optimizableVariable]
                           Options: [1x1 struct]
                      MinObjective: 0.1197
                   XAtMinObjective: [1x2 table]
             MinEstimatedObjective: 0.1213
          XAtMinEstimatedObjective: [1x2 table]
           NumObjectiveEvaluations: 30
                  TotalElapsedTime: 42.8416
                         NextPoint: [1x2 table]
                            XTrace: [30x2 table]
                    ObjectiveTrace: [30x1 double]
                  ConstraintsTrace: []
                     UserDataTrace: {30x1 cell}
      ObjectiveEvaluationTimeTrace: [30x1 double]
                IterationTimeTrace: [30x1 double]
                        ErrorTrace: [30x1 double]
                  FeasibilityTrace: [30x1 logical]
       FeasibilityProbabilityTrace: [30x1 double]
               IndexOfMinimumTrace: [30x1 double]
             ObjectiveMinimumTrace: [30x1 double]
    EstimatedObjectiveMinimumTrace: [30x1 double]

連結制約があるベイズ最適化

連結制約は、目的関数を評価することによってのみ評価できる制約です。このケースでは、目的関数は SVM モデルの交差検証損失です。連結制約は、「サポート ベクターの個数が 100 を超えない」です。モデルの詳細については、bayesopt を使用した交差検証分類器の最適化を参照してください。

分類用のデータを作成します。

rng default
grnpop = mvnrnd([1,0],eye(2),10);
redpop = mvnrnd([0,1],eye(2),10);
redpts = zeros(100,2);
grnpts = redpts;
for i = 1:100
    grnpts(i,:) = mvnrnd(grnpop(randi(10),:),eye(2)*0.02);
    redpts(i,:) = mvnrnd(redpop(randi(10),:),eye(2)*0.02);
end
cdata = [grnpts;redpts];
grp = ones(200,1);
grp(101:200) = -1;
c = cvpartition(200,'KFold',10);
sigma = optimizableVariable('sigma',[1e-5,1e5],'Transform','log');
box = optimizableVariable('box',[1e-5,1e5],'Transform','log');

目的関数は、分割 c における SVM モデルの交差検証損失です。連結制約は、サポート ベクターの個数から 100.5 を減算した値です。このようにすると、100 個のサポート ベクターでは負の制約値、101 個のサポート ベクターでは正の制約値になります。モデルには 200 個のデータ点があるので、連結制約の値の範囲は -99.5 (少なくとも 1 つのサポート ベクターが常にあります) から 99.5 になります。正の値は、制約が満たされないことを意味します。

function [objective,constraint] = mysvmfun(x,cdata,grp,c)
SVMModel = fitcsvm(cdata,grp,'KernelFunction','rbf',...
    'BoxConstraint',x.box,...
    'KernelScale',x.sigma);
cvModel = crossval(SVMModel,'CVPartition',c);
objective = kfoldLoss(cvModel);
constraint = sum(SVMModel.IsSupportVector)-100.5;

このデータを組み込む無名関数として fun を作成して、区分 c と近似データ cdata および grp を目的関数 fun に渡します。関数のパラメーター化 を参照してください。

fun = @(x)mysvmfun(x,cdata,grp,c);

連結制約があることをオプティマイザーが認識できるようにするため、NumCoupledConstraints を 1 に設定します。制約モデルをプロットするようにオプションを設定します。

results = bayesopt(fun,[sigma,box],'IsObjectiveDeterministic',true,...
    'NumCoupledConstraints',1,'PlotFcn',...
    {@plotMinObjective,@plotConstraintModels},...
    'AcquisitionFunctionName','expected-improvement-plus','Verbose',0);

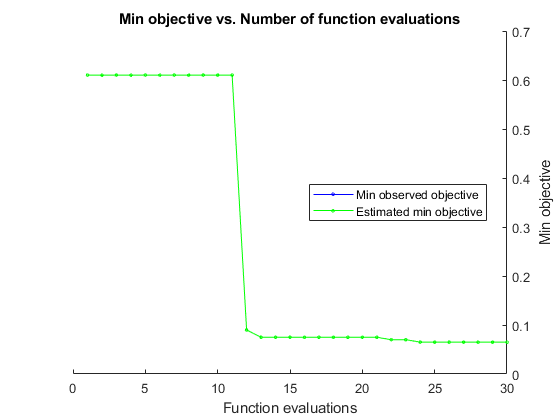
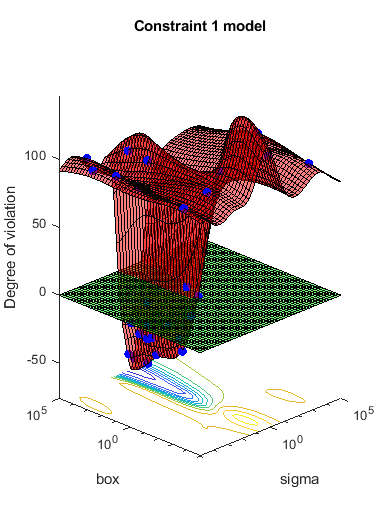
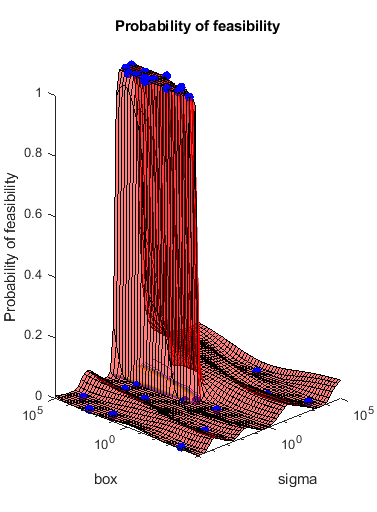
ほとんどの点でサポート ベクターが実行不可能な数になります。

並列ベイズ最適化

目的関数を並列評価することにより、ベイズ最適化を高速化します。

ベイズ最適化の目的関数と変数を準備します。

目的関数は電離層データの交差検証誤差率であり、バイナリ分類問題です。分類器として fitcsvm を使用し、最適化するパラメーターとして BoxConstraint と KernelScale を使用します。

load ionosphere
box = optimizableVariable('box',[1e-4,1e3],'Transform','log');
kern = optimizableVariable('kern',[1e-4,1e3],'Transform','log');
vars = [box,kern];
fun = @(vars)kfoldLoss(fitcsvm(X,Y,'BoxConstraint',vars.box,'KernelScale',vars.kern,...
    'Kfold',5));

並列ベイズ最適化を使用して、交差検証誤差が最小になるパラメーターを求めます。

results = bayesopt(fun,vars,'UseParallel',true);

Copying objective function to workers...
Done copying objective function to workers.

|===============================================================================================================|
| Iter | Active  | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |          box |         kern |
|      | workers | result |             | runtime     | (observed)  | (estim.)    |              |              |
|===============================================================================================================|
|    1 |       2 | Accept |      0.2735 |     0.56171 |     0.13105 |     0.13108 |    0.0002608 |       0.2227 |
|    2 |       2 | Accept |     0.35897 |      0.4062 |     0.13105 |     0.13108 |       3.6999 |       344.01 |
|    3 |       2 | Accept |     0.13675 |     0.42727 |     0.13105 |     0.13108 |      0.33594 |      0.39276 |
|    4 |       2 | Accept |     0.35897 |      0.4453 |     0.13105 |     0.13108 |     0.014127 |       449.58 |
|    5 |       2 | Best   |     0.13105 |     0.45503 |     0.13105 |     0.13108 |      0.29713 |       1.0859 |

|    6 |       6 | Accept |     0.35897 |     0.16605 |     0.13105 |     0.13108 |       8.1878 |        256.9 |

|    7 |       5 | Best   |     0.11396 |     0.51146 |     0.11396 |     0.11395 |       8.7331 |       0.7521 |
|    8 |       5 | Accept |     0.14245 |     0.24943 |     0.11396 |     0.11395 |    0.0020774 |     0.022712 |

|    9 |       6 | Best   |     0.10826 |      4.0711 |     0.10826 |     0.10827 |    0.0015925 |    0.0050225 |

|   10 |       6 | Accept |     0.25641 |      16.265 |     0.10826 |     0.10829 |   0.00057357 |   0.00025895 |

|   11 |       6 | Accept |      0.1339 |      15.581 |     0.10826 |     0.10829 |       1.4553 |     0.011186 |

|   12 |       6 | Accept |     0.16809 |      19.585 |     0.10826 |     0.10828 |      0.26919 |   0.00037649 |

|   13 |       6 | Accept |     0.20513 |      18.637 |     0.10826 |     0.10828 |       369.59 |     0.099122 |

|   14 |       6 | Accept |     0.12536 |     0.11382 |     0.10826 |     0.10829 |       5.7059 |       2.5642 |

|   15 |       6 | Accept |     0.13675 |        2.63 |     0.10826 |     0.10828 |       984.19 |       2.2214 |

|   16 |       6 | Accept |     0.12821 |      2.0743 |     0.10826 |     0.11144 |    0.0063411 |    0.0090242 |

|   17 |       6 | Accept |      0.1339 |      0.1939 |     0.10826 |     0.11302 |   0.00010225 |    0.0076795 |

|   18 |       6 | Accept |     0.12821 |     0.20933 |     0.10826 |     0.11376 |       7.7447 |       1.2868 |

|   19 |       4 | Accept |     0.55556 |      17.564 |     0.10826 |     0.10828 |    0.0087593 |   0.00014486 |
|   20 |       4 | Accept |      0.1396 |      16.473 |     0.10826 |     0.10828 |     0.054844 |     0.004479 |
|===============================================================================================================|
| Iter | Active  | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |          box |         kern |
|      | workers | result |             | runtime     | (observed)  | (estim.)    |              |              |
|===============================================================================================================|
|   21 |       4 | Accept |      0.1339 |     0.17127 |     0.10826 |     0.10828 |       9.2668 |       1.2171 |

|   22 |       4 | Accept |     0.12821 |    0.089065 |     0.10826 |     0.10828 |       12.265 |       8.5455 |

|   23 |       4 | Accept |     0.12536 |    0.073586 |     0.10826 |     0.10828 |       1.3355 |       2.8392 |

|   24 |       4 | Accept |     0.12821 |     0.08038 |     0.10826 |     0.10828 |       131.51 |       16.878 |

|   25 |       3 | Accept |     0.11111 |      10.687 |     0.10826 |     0.10867 |       1.4795 |     0.041452 |
|   26 |       3 | Accept |     0.13675 |     0.18626 |     0.10826 |     0.10867 |       2.0513 |      0.70421 |

|   27 |       6 | Accept |     0.12821 |    0.078559 |     0.10826 |     0.10868 |       980.04 |        44.19 |

|   28 |       5 | Accept |     0.33048 |    0.089844 |     0.10826 |     0.10843 |      0.41821 |       10.208 |
|   29 |       5 | Accept |     0.16239 |     0.12688 |     0.10826 |     0.10843 |       172.39 |       141.43 |

|   30 |       5 | Accept |     0.11966 |     0.14597 |     0.10826 |     0.10846 |       639.15 |        14.75 |

__________________________________________________________
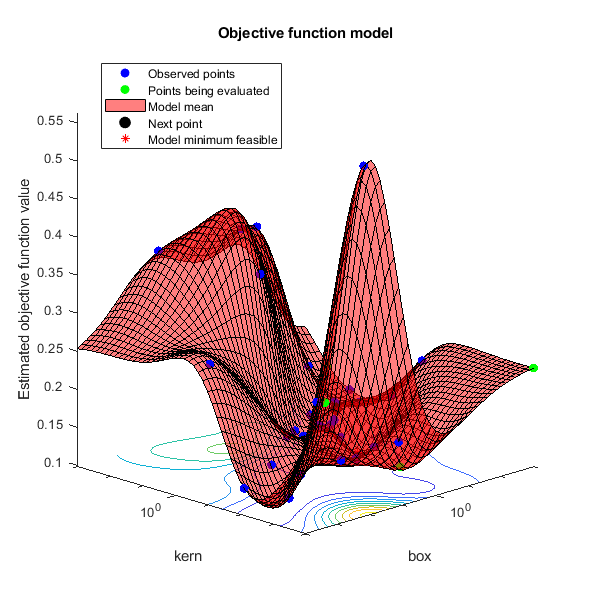
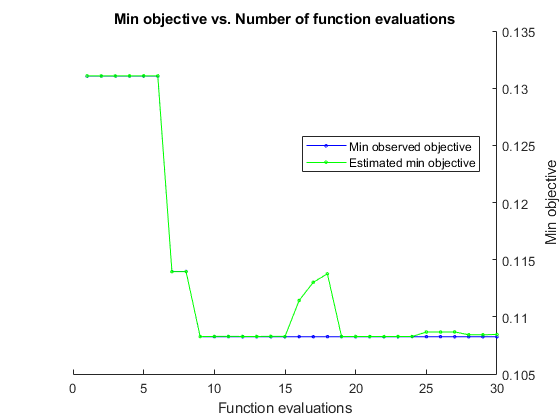
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 48.2085 seconds.
Total objective function evaluation time: 128.3472

Best observed feasible point:
       box         kern   
    _________    _________

    0.0015925    0.0050225

Observed objective function value = 0.10826
Estimated objective function value = 0.10846
Function evaluation time = 4.0711

Best estimated feasible point (according to models):
       box         kern   
    _________    _________

    0.0015925    0.0050225

Estimated objective function value = 0.10846
Estimated function evaluation time = 2.8307

関数 bestPoint を使用して、ベイズ モデル results 内の最良の実行可能点を取得します。既定の基準 min-visited-upper-confidence-interval を使用します。この基準では、目的関数の値に対して信頼区間の上限を最小化する探索済みの点が最良の実行可能点になります。

zbest = bestPoint(results)

zbest=1×2 table
       box         kern   
    _________    _________

    0.0015925    0.0050225

テーブル zbest には、名前と値のペアの引数 'BoxConstraint' および 'KernelScale' に最適な推定値が格納されます。これらの値を使用して、最適化された新しい分類器に学習をさせます。

Mdl = fitcsvm(X,Y,'BoxConstraint',zbest.box,'KernelScale',zbest.kern);

最適なパラメーターが Mdl に含まれていることを確認します。

Mdl.BoxConstraints(1)

ans = 0.0016

Mdl.KernelParameters.Scale

ans = 0.0050

入力引数

fun — 目的関数

関数ハンドル | Value が関数ハンドルである parallel.pool.Constant

目的関数。関数ハンドルを指定するか、名前と値のペア UseParallel が true である場合は、Value が関数ハンドルである parallel.pool.Constant (Parallel Computing Toolbox) を指定します。通常 fun は、学習を制御するための調整可能なハイパーパラメーターがある、機械学習モデルの損失の尺度 (誤分類誤差など) を返します。fun のシグネチャは次のとおりです。

objective = fun(x)
% or
[objective,constraints] = fun(x)
% or
[objective,constraints,UserData] = fun(x)

fun は、1 行 D 列の変数値テーブル x を受け入れ、目的関数値 fun(x) を表す実数スカラー objective を返します。

オプションとして、fun は以下も返します。

• constraints。連結制約違反が格納されている実数ベクトル。定義については、連結制約を参照してください。constraint(j) > 0 の場合、制約 j に違反しています。constraint(j) < 0 の場合、制約 j は満たされています。

• UserData。任意のタイプ (スカラー、行列、構造体、オブジェクトなど) のエンティティ。UserData を使用するカスタム プロット関数の例については、カスタム プロット関数の作成を参照してください。

bayesopt における parallel.pool.Constant の使用の詳細については、ワーカーへの目的関数の配置を参照してください。

例: @objfun

データ型: function_handle

vars — 変数の説明

調整対象のハイパーパラメーターを定義する optimizableVariable オブジェクトのベクトル

変数の説明。調整対象のハイパーパラメーターを定義する optimizableVariable オブジェクトのベクトルを指定します。

例: [X1,X2]。ここで X1 と X2 は optimizableVariable オブジェクト

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後ろにする必要がありますが、ペアの順序は関係ありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: results = bayesopt(fun,vars,'AcquisitionFunctionName','expected-improvement-plus')

アルゴリズムの制御

AcquisitionFunctionName — 次の評価点を選択するための関数

'expected-improvement-per-second-plus' (既定値) | 'expected-improvement' | 'expected-improvement-plus' | 'expected-improvement-per-second' | 'lower-confidence-bound' | 'probability-of-improvement'

次の評価点を選択するための関数。リストされている選択肢のいずれかを指定します。

オブジェクト関数のランタイムによって最適化が異なるので、名前に per-second が含まれている獲得関数は、再現性がある結果を生成しません。名前に plus が含まれている獲得関数は、領域を過剰利用している場合に動作を変更します。詳細は、獲得関数のタイプを参照してください。

例: 'AcquisitionFunctionName','expected-improvement-per-second'

IsObjectiveDeterministic — 確定的目的関数の指定

false (既定値) | true

確定的目的関数の指定。false または true を指定します。fun が確率的である (つまり同じ x に対して異なる値を fun(x) が返す可能性がある) 場合は、IsObjectiveDeterministic を false に設定します。この場合、bayesopt は最適化時にノイズ レベルを推定します。

例: 'IsObjectiveDeterministic',true

データ型: logical

ExplorationRatio — 調査の傾向

0.5 (既定値) | 正の実数

調査の傾向。正の実数を指定します。'expected-improvement-plus' および 'expected-improvement-per-second-plus' の獲得関数に適用されます。プラスを参照してください。

例: 'ExplorationRatio',0.2

データ型: double

GPActiveSetSize — GPActiveSetSize 個以下の点へのガウス過程モデルの当てはめ

300 (既定値) | 正の整数

GPActiveSetSize 個以下の点へのガウス過程モデルの当てはめ。正の整数を指定します。bayesopt が GPActiveSetSize 個を超える点に到達した場合、GP モデルを使用する以後の反復では GPActiveSetSize 個の点にモデルが当てはめられます。bayesopt は、到達した点の中から無作為な点を一様に非復元抽出で選択します。使用する点の数が少なくなると GP モデルの当てはめが高速になりますが、代償として精度が低下する可能性があります。

例: 'GPActiveSetSize',80

データ型: double

UseParallel — 並列計算

false (既定値) | true

並列計算。false (並列計算を行わない) または true (並列計算を行う) を指定します。並列計算には Parallel Computing Toolbox™ が必要です。

bayesopt は並列ワーカー上で、目的関数の並列評価を同時実行します。アルゴリズムの詳細については、並列ベイズ最適化を参照してください。

例: 'UseParallel',true

データ型: logical

ParallelMethod — 並列ワーカーの目的関数値への補定法

'clipped-model-prediction' (既定値) | 'model-prediction' | 'max-observed' | 'min-observed'

並列ワーカーの目的関数値への補定法。'clipped-model-prediction'、'model-prediction'、'max-observed' または 'min-observed' を指定します。新しい評価対象点を生成するため、bayesopt はワーカーで評価されている点を含むすべての点にガウス過程を当てはめます。ガウス過程を当てはめるため、bayesopt は現在ワーカー上にある点に目的関数の値を補完します。ParallelMethod は、補定に使用する方法を指定します。

• 'clipped-model-prediction' — 次の数量の最大値を補定します。

  • 点 x におけるガウス過程予測の平均

  • 到達した実行可能点で観測された最小の目的関数

  • すべての実行可能点における最小のモデル予測

• 'model-prediction' — 点 x におけるガウス過程予測の平均を補定します。

• 'max-observed' — 実行可能点で観測された目的関数の最大値を補定します。

• 'min-observed' — 実行可能点で観測された目的関数の最小値を補定します。

例: 'ParallelMethod','max-observed'

MinWorkerUtilization — アクティブな並列ワーカーの個数の許容誤差

floor(0.8*Nworkers) (既定値) | 正の整数

アクティブな並列ワーカーの個数の許容誤差。正の整数を指定します。bayesopt は、評価対象の点を割り当てた後で、新しい割り当て対象の点を計算する前に、アクティブなワーカーの個数が MinWorkerUtilization 未満であるかどうかをチェックします。そうである場合、bayesopt は範囲内の無作為な点をすべての使用可能なワーカーに割り当てます。それ以外の場合、bayesopt は 1 つのワーカーについて最適な点を計算します。bayesopt が無作為な点を作成する速度は点を当てはめる場合よりはるかに高速なので、この動作によりワーカーの使用率が向上しますが、点が適切ではなくなる可能性があるという代償があります。詳細については、並列ベイズ最適化を参照してください。

例: 'MinWorkerUtilization',3

データ型: double

開始と停止

MaxObjectiveEvaluations — 目的関数の評価制限

30 (既定値) | 正の整数

目的関数の評価制限。正の整数を指定します。

例: 'MaxObjectiveEvaluations',60

データ型: double

MaxTime — 制限時間

Inf (既定値) | 正の実数

制限時間。正の実数を指定します。制限時間の単位は、tic と toc によって測定される秒です。

bayesopt は関数評価を中断させないため、実行時間が MaxTime を超える可能性があります。

例: 'MaxTime',3600

データ型: double

NumSeedPoints — 初期評価点の個数

4 (既定値) | 正の整数

初期評価点の個数。正の整数を指定します。bayesopt は、各変数の Transform の設定に従って ('none' の場合は均等に、'log' の場合は対数間隔で)、変数の範囲内で評価点を無作為に選択します。

例: 'NumSeedPoints',10

データ型: double

制約

XConstraintFcn — 変数の確定的制約

[] (既定値) | 関数ハンドル

変数の確定的制約。関数ハンドルを指定します。

詳細は、確定的制約 — XConstraintFcnを参照してください。

例: 'XConstraintFcn',@xconstraint

データ型: function_handle

ConditionalVariableFcn — 変数の条件付き制約

[] (既定値) | 関数ハンドル

変数の条件付き制約。関数ハンドルを指定します。

詳細は、条件付き制約 — ConditionalVariableFcnを参照してください。

例: 'ConditionalVariableFcn',@condfun

データ型: function_handle

NumCoupledConstraints — 連結制約の個数

0 (既定値) | 正の整数

連結制約の個数。正の整数を指定します。詳細は、連結制約を参照してください。

メモ

連結制約がある場合、NumCoupledConstraints は必須です。

例: 'NumCoupledConstraints',3

データ型: double

AreCoupledConstraintsDeterministic — 連結制約が確定的かどうかの指標

すべての連結制約に対して true (既定値) | logical ベクトル

連結制約が確定的かどうかの指標。長さ NumCoupledConstraints の logical ベクトルを指定します。詳細は、連結制約を参照してください。

例: 'AreCoupledConstraintsDeterministic',[true,false,true]

データ型: logical

レポート、プロットおよび中断

Verbose — コマンド ラインの表示レベル

1 (既定値) | 0 | 2

コマンド ラインの表示レベル。0、1 または 2 を指定します。

• 0 — コマンド ラインの表示を行いません。

• 1 — 各反復について、反復回数、結果レポート (次の段落を参照)、目的関数のモデル、目的関数の評価時間、観測された目的関数の最良 (最小) 値、目的関数の最良 (最小) 推定値、および観測された制約値 (存在する場合) を表示します。並列で最適化を行う場合、ジョブを次のワーカーに割り当てた後でカウントしたアクティブなワーカーの個数を示す列も表示に含まれます。

  各反復の結果レポートは以下のいずれかになります。

  • Accept — 目的関数が有限値を返し、すべての制約が満たされています。

  • Best — 制約が満たされており、目的関数は実行可能点の最小値を返します。

  • Error — 有限の実数スカラーではない値を目的関数が返しました。

  • Infeas — 少なくとも 1 つの制約に違反しています。

• 2 — 1 と同じ情報に加えて、次の点を選択するための時間、モデルを当てはめた時間、"plus" の獲得関数で過剰利用が判断されたかどうか、並列利用率が低いため無作為な点に並列ワーカーが割り当てられているかどうかなどの診断情報も表示します。

例: 'Verbose',2

データ型: double

OutputFcn — 各反復後に呼び出される関数

{} (既定値) | 関数ハンドル | 関数ハンドルの cell 配列

各反復後に呼び出される関数。関数ハンドルまたは関数ハンドルの cell 配列を指定します。出力関数では、ソルバーを停止させることができ、変数の作成やプロットなど任意の計算を実行できます。複数の出力関数を指定するには、関数ハンドルの cell 配列を使用します。

2 つの組み込み出力関数があります。

• @assignInBase — 各反復で BayesianOptimization のインスタンスを構築し、ベース ワークスペース内の変数に割り当てます。名前と値のペア SaveVariableName を使用して変数名を選択します。

• @saveToFile — 各反復で BayesianOptimization のインスタンスを構築し、現在のフォルダー内のファイルに保存します。名前と値のペア SaveFileName を使用してファイル名を選択します。

独自の出力関数を作成できます。詳細は、ベイズ最適化の出力関数を参照してください。

例: 'OutputFcn',{@saveToFile @myOutputFunction}

データ型: cell | function_handle

SaveFileName — 出力関数 @saveToFile のファイル名

'BayesoptResults.mat' (既定値) | 文字ベクトル | string スカラー

出力関数 @saveToFile のファイル名。文字ベクトルまたは string スカラーを指定します。ファイル名には '../optimizations/September2.mat' などのパスを含めることができます。

例: 'SaveFileName','September2.mat'

データ型: char | string

SaveVariableName — 出力関数 @assignInBase の変数名

'BayesoptResults' (既定値) | 文字ベクトル | string スカラー

出力関数 @assignInBase の変数名。文字ベクトルまたは string スカラーを指定します。

例: 'SaveVariableName','September2Results'

データ型: char | string

PlotFcn — 各反復後に呼び出されるプロット関数

{@plotObjectiveModel,@plotMinObjective} (既定値) | 'all' | 関数ハンドル | 関数ハンドルの cell 配列

各反復後に呼び出されるプロット関数。'all'、関数ハンドル、または関数ハンドルの cell 配列を指定します。プロット関数では、ソルバーを停止させることができ、変数の作成など任意の計算をプロットに加えて実行できます。

プロット関数を使用しない場合は [] を指定します。

'all' の場合、すべての組み込みプロット関数が呼び出されます。複数のプロット関数を指定するには、関数ハンドルの cell 配列を使用します。

組み込みプロット関数を次の表に示します。

モデル プロット — D ≤ 2 の場合に適用	説明
@plotAcquisitionFunction	獲得関数の表面をプロットします。
@plotConstraintModels	各制約モデルの表面をプロットします。負の値は実行可能点を示します。 P (実行可能) 表面もプロットします。 存在する場合は –1 から 1 の範囲のエラー モデルもプロットします。負の値はモデルでエラーが発生する可能性が低いことを、正の値はエラーが発生する可能性が高いことを意味します。モデルは以下のようになります。 Plotted error = 2*Probability(error) – 1.
@plotObjectiveEvaluationTimeModel	目的関数の評価時間モデルの表面をプロットします。
@plotObjectiveModel	fun モデルの表面、最小値の推定位置、および次に評価する予定になっている点の位置をプロットします。1 次元問題の場合、平均関数から 1 信頼区間分上下と平均から 1 ノイズ標準偏差分上下に包絡線をプロットします。

トレース プロット — すべての D に適用	説明
@plotObjective	観測された各関数値と関数評価の個数の関係をプロットします。
@plotObjectiveEvaluationTime	観測された各関数評価の実行時間と関数評価の個数の関係をプロットします。
@plotMinObjective	観測および推定された最小の関数値と関数評価の個数の関係をプロットします。
@plotElapsedTime	最適化の合計経過時間、関数評価の合計時間、モデリングおよび点選択の合計時間という 3 つの曲線を関数評価の個数に対する関係としてプロットします。

独自のプロット関数を作成できます。詳細は、ベイズ最適化のプロット関数を参照してください。

メモ

連結制約がある場合、反復表示とプロット関数は次のような直観的ではない結果を与える可能性があります。

• "最小目的" のプロットが増加する。

• 最適化において、以前に実行可能点が示された場合でも、問題が実行不可能であると宣言される場合がある。

このようになるのは、点が実行可能かどうかの判断が最適化の進行に応じて変化する可能性があるためです。bayesopt は制約モデルに関して実行可能性を判断しますが、このモデルは bayesopt が点を評価すると変化します。したがって、最小の点が後から実行不可能と判断された場合は "最小目的" プロットが増加し、反復表示には、後から実行不可能と判断される実行可能点が表示される可能性があります。

例: 'PlotFcn','all'

データ型: char | string | cell | function_handle

初期化

InitialX — 初期評価点

範囲内にある NumSeedPoints 行 D 列のランダムな初期点 (既定値) | N 行 D 列のテーブル

初期評価点。N 行 D 列のテーブルを指定します。N は評価点の個数、D は変数の個数です。

メモ

InitialX のみを指定した場合、評価対象の初期点として解釈されます。目的関数は InitialX で評価されます。

他の初期化パラメーターも指定した場合、InitialX は事前関数評価データとして解釈されます。目的関数は評価されません。欠損値は NaN に設定されます。

データ型: table

InitialObjective — InitialX に対応する目的関数の値

[] (既定値) | 長さ N のベクトル

InitialX に対応する目的関数の値。長さ N のベクトルを指定します。N は評価点の個数です。

例: 'InitialObjective',[17;-3;-12.5]

データ型: double

InitialConstraintViolations — 連結制約の制約違反

[] (既定値) | N 行 K 列の行列

連結制約の制約違反。N 行 K 列の行列を指定します。N は評価点の個数、K は連結制約の個数です。詳細は、連結制約を参照してください。

データ型: double

InitialErrorValues — InitialX のエラー

[] (既定値) | 入力が -1 または 1 である長さ N のベクトル

InitialX のエラー。入力が -1 または 1 である長さ N のベクトルを指定します。N は評価点の個数です。エラーなしの場合は -1、エラーの場合は 1 を指定します。

例: 'InitialErrorValues',[-1,-1,-1,-1,1]

データ型: double

InitialUserData — InitialX に対応する初期データ

[] (既定値) | 長さ N の cell ベクトル

InitialX に対応する初期データ。長さ N の cell ベクトルを指定します。N は評価点の個数です。

例: 'InitialUserData',{2,3,-1}

データ型: cell

InitialObjectiveEvaluationTimes — InitialX における目的関数の評価時間

[] (既定値) | 長さ N のベクトル

InitialX における目的関数の評価時間。長さ N のベクトルを指定します。N は評価点の個数です。時間の単位は秒です。

データ型: double

InitialIterationTimes — 最初の N 回の反復の時間

{} (既定値) | 長さ N のベクトル

最初の N 回の反復の時間。長さ N のベクトルを指定します。N は評価点の個数です。時間の単位は秒です。

データ型: double

出力引数

results — ベイズ最適化の結果

BayesianOptimization オブジェクト

ベイズ最適化の結果。BayesianOptimization オブジェクトとして返されます。

詳細

連結制約

連結制約は、その値が目的関数の計算に由来する制約です。連結制約を参照してください。

ヒント

• 次のいずれかの条件が存在する場合、ベイズ最適化は再現可能ではありません。

  • 'expected-improvement-per-second' のような、名前に per-second が含まれている獲得関数を指定する。修飾子 per-second は、最適化が目的関数の実行時に依存することを示します。詳細は、獲得関数のタイプを参照してください。

  • ベイズ最適化を並列実行するよう指定する。並列でのタイミングに再現性がないため、並列ベイズ最適化で再現性のある結果が生成されるとは限りません。詳細は、並列ベイズ最適化を参照してください。

拡張機能

自動並列サポート

Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

並列実行するには、この関数を呼び出すときに名前と値の引数 UseParallel を true に設定します。

並列計算の全般的な情報については、自動並列サポートを使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2016b で導入

参考

BayesianOptimization | bestPoint | optimizableVariable

トピック

• bayesopt を使用した交差検証分類器の最適化
• ベイズ最適化のアルゴリズム