ベイズ最適化の制約
範囲
bayesopt では、すべての変数で範囲が有限である必要があります (性質上、categorical 変数は可能な値に限定されます)。実数値または整数値の変数の下限と上限は optimizableVariable で渡します。
bayesopt は、これらの範囲を使用して均等または対数スケールで点を抽出します。抽出のスケールは optimizableVariable で設定します。
たとえば、変数 X1 を対数スケールで 1e-6 と 1e3 の間の値に制約するには、次のようにします。
xvar = optimizableVariable('X1',[1e-6,1e3],'Transform','log')
bayesopt は端点を範囲に含めます。したがって、対数変換される実数の変数の下限として 0 を使用することはできません。
ヒント
対数変換される実数の変数の下限としてゼロを使用するには、下限を 1 に設定し、目的関数の内部で x-1 を使用します。
対数変換される整数値の変数については、下限として 0 を使用できます。整数値の変数の下限が 0 の場合、変数のサンプリング範囲に 0 を含めるために、関数 log の代わりに関数 log1p を使用して対数スケール間隔が作成されます。log1p は、入力 x に対して log(1+x) を返す関数です。
確定的制約 — XConstraintFcn
問題が有効、または明確に定義されている状態が "実行可能領域" と呼ばれる特定の領域内の点についてのみの場合があります。確定的制約は、点が実行可能な場合は true を、実行不可能な場合は false を返す確定的関数です。したがって、確定的制約は確率的ではありません。また、点のグループではなく個々の点の関数です。
ヒント
最適化を矩形領域に制限するには、確定的制約ではなく optimizableVariable の範囲を使用する方が効率的です。
確定的制約関数を記述するには、次のシグネチャを使用します。
tf = xconstraint(X)
Xは、幅が D で高さが任意のテーブルです。tfは、X(i,:)が実行可能な場合にのみtf(i) = trueになる論理列ベクトルです。
確定的制約関数は、bayesopt の名前と値の引数 XConstraintFcn で渡します。以下に例を示します。
results = bayesopt(fun,vars,'XConstraintFcn',@xconstraint)
bayesopt は数千個の点に対して確定的制約を評価するので、制約関数をベクトル化すると実行が高速になります。ベクトル化を参照してください。
たとえば、'x1' および 'x2' という名前の変数は、ベクトル [x1 x2] のノルムが 6 未満で x1 <= x2 の場合に実行可能であるとします。次の制約関数はこれらの制約を評価します。
function tf = xconstraint(X)
tf1 = sqrt(X.x1.^2 + X.x2.^2) < 6;
tf2 = X.x1 <= X.x2;
tf = tf1 & tf2;条件付き制約 — ConditionalVariableFcn
条件付き制約は、次の 2 つの条件のいずれかを適用する関数です。
一部の変数が特定の値の場合、他の変数が特定の値になる。
一部の変数が特定の値の場合に、他の変数が
NaN(カテゴリカル変数の場合は<undefined>) 値になる。
条件付き制約を指定するには、bayesopt の名前と値の引数 ConditionalVariableFcn を @condvariablefcn などの関数ハンドルに設定します。@condvariablefcn の関数のシグネチャは次のようになっていなければなりません。
Xnew = condvariablefcn(X)
Xは、幅がDで高さが任意のテーブルです。Xnewは、Xと同じ型およびサイズのテーブルです。
condvariablefcn では、X に等しくなるように Xnew を設定しますが、さらに Xnew の各行の該当する変数を制約にかなった値に設定します。
メモ
条件付き制約と確定的制約の両方がある場合、bayesopt は条件付き制約を先に適用します。したがって、条件付き制約関数で変数を NaN または <undefined> に設定する可能性がある場合、これらの値を確定的制約関数で正しく処理できるようにする必要があります。
条件付き制約は、変数値を確実に実体的にします。したがって、まず bayesopt は条件付き制約を適用し、渡されるすべての値を実体的なものとします。
変数値を設定する条件付き制約
fitcdiscr を使用して分類を最適化しており、名前と値の引数 'DiscrimType' および 'Gamma' の両方について最適化しているとします。'DiscrimType' が二次タイプのいずれかである場合、'Gamma' が 0 でないとソルバーでエラーが発生します。このようなケースでは、次の条件付き制約関数を使用します。
function XTable = fitcdiscrCVF(XTable) % Gamma must be 0 if discrim type is a quadratic XTable.Gamma(ismember(XTable.DiscrimType, {'quadratic',... 'diagQuadratic','pseudoQuadratic'})) = 0; end
変数を NaN に設定する条件付き制約
fitcsvm を使用して分類を最適化しており、名前と値の引数 'KernelFunction' および 'PolynomialOrder' の両方について最適化しているとします。'KernelFunction' が 'polynomial' ではない場合、'PolynomialOrder' の設定は適用されません。次の関数は、この条件付き制約を強制します。
function Xnew = condvariablefcn(X) Xnew = X; Xnew.PolynomialOrder(Xnew.KernelFunction ~= 'polynomial') = NaN;
次のようにすると、コードの行数を少なくすることができます。
function X = condvariablefcn(X) X.PolynomialOrder(X.KernelFunction ~= 'polynomial') = NaN;
さらに、'PolynomialOrder' の値が NaN である場合は名前と値の引数 'PolynomialOrder' を fitcsvm に渡さない目的関数を定義します。
fun = @(X)mysvmfun(X,predictors,responce,c) function objective = mysvmfun(X,predictors,response,c) args = {predictors,response, ... 'CVPartition',c, ... 'KernelFunction',X.KernelFunction}; if ~isnan(X.PolynomialOrder) args = [args,{'PolynomialOrder',X.PolynomialOrder}]; end objective = kfoldLoss(fitcsvm(args{:})); end
連結制約
"連結制約" は、目的関数を呼び出すことによってのみ評価できる制約です。この制約は、確率的にも確定的にもすることができます。これらの制約値は、2 番目の引数で目的関数から返します。ベイズ最適化の目的関数を参照してください。
目的関数は、各連結制約について 1 つずつエントリがある、連結制約の数値ベクトルを返します。各エントリで、負の値は制約が満たされること (実行可能とも呼びます) を示します。正の値は制約が満たされないこと (実行不可能) を示します。
bayesopt は、エラー制約と呼ばれる連結制約をすべての実行で自動的に作成します。この制約により、目的関数の評価でエラーが発生する点を bayesopt でモデル化できます。詳細については、目的関数のエラーと predictError を参照してください。
エラー制約に加えて連結制約がある場合、
bayesoptの呼び出しに、名前と値の引数NumCoupledConstraintsを含めます (必須)。この数にエラー制約は含めないでください。いずれかの連結制約が確率的である場合、名前と値の引数
AreCoupledConstraintsDeterministicを使用し、確率的制約についてfalseを渡します。
各反復における連結制約の値を確認するには、bayesopt の名前と値の引数 Verbose を 1 または 2 に設定します。
メモ
連結制約がある場合、反復表示とプロット関数は次のような直観的ではない結果を与える可能性があります。
"最小目的" のプロットが増加します。
最適化において、以前に実行可能点が示された場合でも、問題が実行不可能であると宣言される場合があります。
このようになるのは、点が実行可能かどうかの判断が最適化の進行に応じて変化する可能性があるためです。bayesopt は制約モデルに関して実行可能性を判断しますが、このモデルは bayesopt が点を評価すると変化します。したがって、最小の点が後から実行不可能と判断された場合は "最小目的" プロットが増加し、反復表示には、後から実行不可能と判断される実行可能点が表示される可能性があります。
たとえば、連結制約があるベイズ最適化を参照してください。
連結制約があるベイズ最適化
連結制約は、目的関数を評価することによってのみ評価できる制約です。このケースでは、目的関数は SVM モデルの交差検証損失です。連結制約は、「サポート ベクターの個数が 100 を超えない」です。モデルの詳細については、bayesopt を使用した交差検証分類器の最適化を参照してください。
分類用のデータを作成します。
rng default grnpop = mvnrnd([1,0],eye(2),10); redpop = mvnrnd([0,1],eye(2),10); redpts = zeros(100,2); grnpts = redpts; for i = 1:100 grnpts(i,:) = mvnrnd(grnpop(randi(10),:),eye(2)*0.02); redpts(i,:) = mvnrnd(redpop(randi(10),:),eye(2)*0.02); end cdata = [grnpts;redpts]; grp = ones(200,1); grp(101:200) = -1; c = cvpartition(200,'KFold',10); sigma = optimizableVariable('sigma',[1e-5,1e5],'Transform','log'); box = optimizableVariable('box',[1e-5,1e5],'Transform','log');
目的関数は、分割 c における SVM モデルの交差検証損失です。連結制約は、サポート ベクターの個数から 100.5 を減算した値です。このようにすると、100 個のサポート ベクターでは負の制約値、101 個のサポート ベクターでは正の制約値になります。モデルには 200 個のデータ点があるので、連結制約の値の範囲は -99.5 (少なくとも 1 つのサポート ベクターが常にあります) から 99.5 になります。正の値は、制約が満たされないことを意味します。
function [objective,constraint] = mysvmfun(x,cdata,grp,c) SVMModel = fitcsvm(cdata,grp,'KernelFunction','rbf',... 'BoxConstraint',x.box,... 'KernelScale',x.sigma); cvModel = crossval(SVMModel,'CVPartition',c); objective = kfoldLoss(cvModel); constraint = sum(SVMModel.IsSupportVector)-100.5;
このデータを組み込む無名関数として fun を作成して、区分 c と近似データ cdata および grp を目的関数 fun に渡します。関数のパラメーター化 を参照してください。
fun = @(x)mysvmfun(x,cdata,grp,c);
連結制約があることをオプティマイザーが認識できるようにするため、NumCoupledConstraints を 1 に設定します。制約モデルをプロットするようにオプションを設定します。
results = bayesopt(fun,[sigma,box],'IsObjectiveDeterministic',true,... 'NumCoupledConstraints',1,'PlotFcn',... {@plotMinObjective,@plotConstraintModels},... 'AcquisitionFunctionName','expected-improvement-plus','Verbose',0);
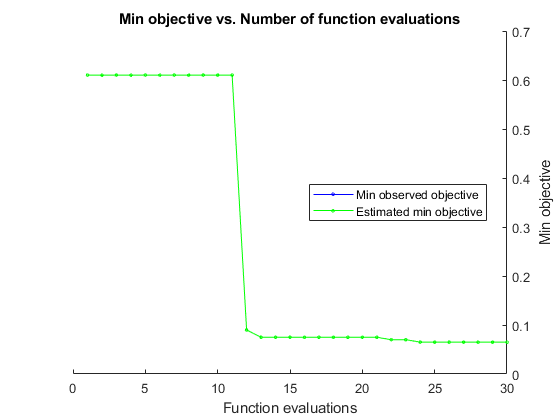
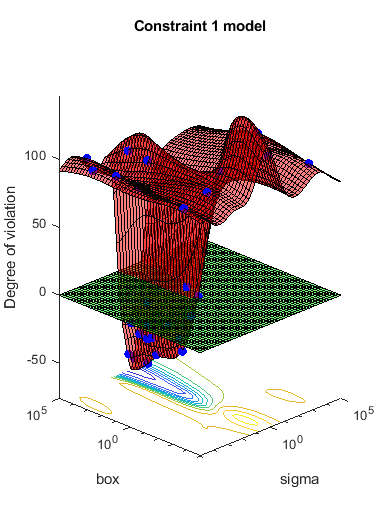
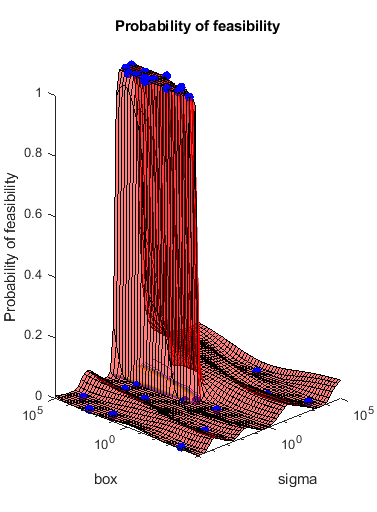
ほとんどの点でサポート ベクターが実行不可能な数になります。
参考
bayesopt | optimizableVariable