predictError

一連の点における誤差値の予測

ページ内をすべて折りたたむ

構文

error = predictError(results,XTable)
[error,sigma] = predictError(results,XTable)

説明

error = predictError(results,XTable) は、XTable 内の点における誤差連結制約の事後平均を返します。

例

[error,sigma] = predictError(results,XTable) は、事後標準偏差も返します。

例

すべて折りたたむ

スクリプトを開く

この例では、評価点のノルムが 2 より大きい場合にエラーをスローする関数を最適化する方法を示します。目的関数のエラー モデルはこの動作を学習します。

-5 ～ 5 の範囲にある x1 および x2 という名前の変数を作成します。

var1 = optimizableVariable('x1',[-5,5]);
var2 = optimizableVariable('x2',[-5,5]);
vars = [var1,var2];

x = [x1,x2] のノルムが 2 より大きい場合、次の目的関数はエラーをスローます。

function f = makeanerror(x)
f = x.x1 - x.x2 - sqrt(4-x.x1^2-x.x2^2);


fun = @makeanerror;

誤差モデルと最小目的関数を最適化の進行に応じてプロットします。誤差モデルに十分に学習をさせるため、60 回の反復で最適化します。再現性を得るために、乱数シードを設定し、'expected-improvement-plus' の獲得関数を使用します。

rng default
results = bayesopt(fun,vars,'Verbose',0,'MaxObjectiveEvaluations',60,...
    'AcquisitionFunctionName','expected-improvement-plus',...
    'PlotFcn',{@plotMinObjective,@plotConstraintModels});

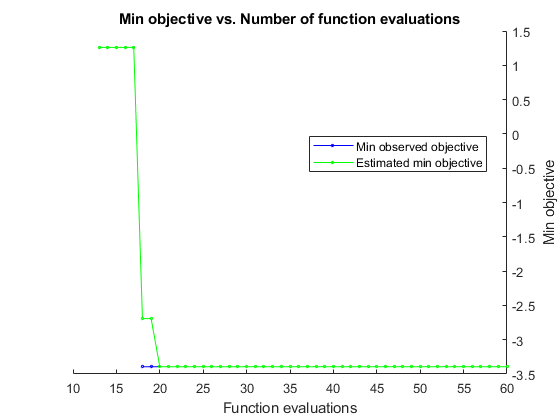
直線 x1 = x2 の点における誤差を予測します。誤差モデルが完全であれば、x のノルムが 2 を超えないすべての点で値は -1、他のすべての点で 1 になります。

x1 = (-5:0.5:5)';
x2 = x1;
XTable = table(x1,x2);
error = predictError(results,XTable);
normx = sqrt(x1.^2 + x2.^2);
[XTable,table(normx,error)]

ans =

  21x4 table

     x1      x2      normx       error  
    ____    ____    _______    _________

      -5      -5     7.0711      0.94663
    -4.5    -4.5      6.364      0.97396
      -4      -4     5.6569      0.99125
    -3.5    -3.5     4.9497       1.0033
      -3      -3     4.2426       1.0018
    -2.5    -2.5     3.5355      0.99627
      -2      -2     2.8284       1.0043
    -1.5    -1.5     2.1213      0.89886
      -1      -1     1.4142       0.4746
    -0.5    -0.5    0.70711    0.0042389
       0       0          0     -0.16004
     0.5     0.5    0.70711    -0.012397
       1       1     1.4142      0.30187
     1.5     1.5     2.1213      0.88588
       2       2     2.8284       1.0872
     2.5     2.5     3.5355        0.997
       3       3     4.2426      0.99861
     3.5     3.5     4.9497      0.98894
       4       4     5.6569      0.98941
     4.5     4.5      6.364      0.98956
       5       5     7.0711      0.95549

入力引数

すべて折りたたむ

ベイズ最適化の結果。BayesianOptimization オブジェクトを指定します。

予測点。列数が D のテーブルを指定します。D は、問題に含まれている変数の個数です。これらの点で予測が実行されます。

データ型: table

出力引数

すべて折りたたむ

誤差連結制約の平均。N 行 1 列のベクトルとして返されます。N は XTable の行数です。この平均は、XTable 内の点における誤差連結制約の事後平均です。

目的関数が有限の実数スカラー以外を返した場合、bayesopt は目的関数がエラーを返したと見なします。目的関数のエラーを参照してください。

誤差連結制約の標準偏差。N 行 1 列のベクトルとして返されます。N は XTable の行数です。

バージョン履歴

R2016b で導入

参考

|