Main Content

このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

bayesopt を使用した交差検証分類器の最適化

ライブ スクリプトを開く

この例では、関数 bayesopt を使用して SVM 分類を最適化する方法を示します。

あるいは、名前と値の引数 OptimizeHyperparameters を使用して分類器を最適化できます。例については、ベイズ最適化の使用による分類器の当てはめの最適化を参照してください。

データの生成

この分類は、混合ガウス モデルによる点の位置に作用します。モデルの詳細については、The Elements of Statistical Learning, Hastie, Tibshirani, and Friedman (2009) の 17 ページを参照してください。このモデルでは、平均 (1,0) および単位分散をもつ 2 次元の独立した正規分布になっている 10 個の基底点をはじめに "green" クラスについて生成します。また、平均 (0,1) と単位分散による 2 次元の独立した正規として分布される "red" クラスにも、10 個の基底点が生成されます。クラス (green と red) ごとに、次のように 100 個の無作為な点を生成します。

  1. 適切な色の基底点 m を一様にランダムに選択します。

  2. 平均 m と分散 I/5 (I は 2 行 2 列の単位行列) をもつ 2 次元正規分布を使用して、独立した無作為な点を生成します。最適化のアドバンテージをより明確に示すため、この例では I/50 という分散を使用します。

クラスごとに 10 個の基底点を生成します。 

rng('default') % For reproducibility
grnpop = mvnrnd([1,0],eye(2),10);
redpop = mvnrnd([0,1],eye(2),10);

基底点を表示します。

plot(grnpop(:,1),grnpop(:,2),'go')
hold on
plot(redpop(:,1),redpop(:,2),'ro')
hold off

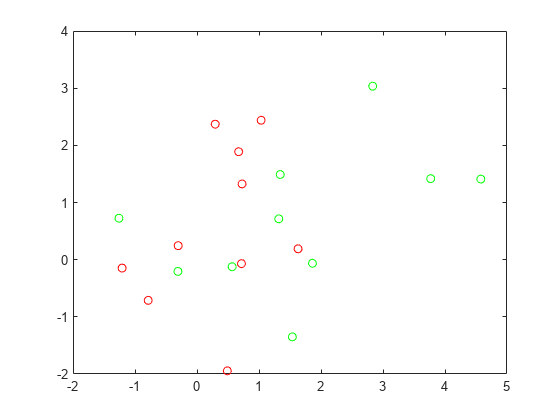
Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

赤の基底点の一部が緑の基底点の近くにあるため、位置のみによるデータ点の分類は難しいかもしれません。

各クラスについて 100 個ずつのデータ点を生成します。

redpts = zeros(100,2);grnpts = redpts;
for i = 1:100
    grnpts(i,:) = mvnrnd(grnpop(randi(10),:),eye(2)*0.02);
    redpts(i,:) = mvnrnd(redpop(randi(10),:),eye(2)*0.02);
end

データ点を表示します。

figure
plot(grnpts(:,1),grnpts(:,2),'go')
hold on
plot(redpts(:,1),redpts(:,2),'ro')
hold off

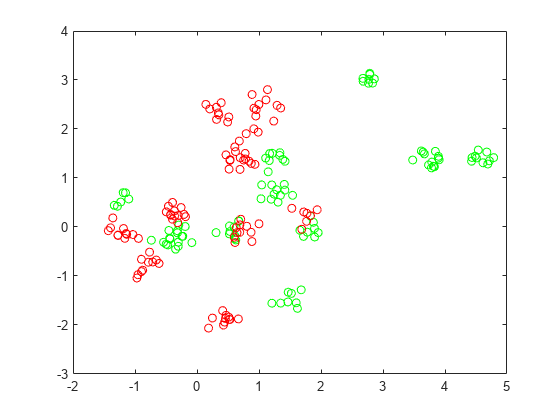
Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

分類用のデータの準備

データを 1 つの行列に格納し、各点のクラスにラベルを付けるベクトル grp を作成します。1 は green クラスを示し、-1 は red クラスを示します。

cdata = [grnpts;redpts];
grp = ones(200,1);
grp(101:200) = -1;

交差検証の準備

交差検証用の分割を設定します。これにより、各ステップで最適化に使用される学習セットとテスト セットとが決まります。

c = cvpartition(200,'KFold',10);

ベイズ最適化用の変数の準備

入力として z = [rbf_sigma,boxconstraint] を受け入れ z の交差検証損失値を返す関数を設定します。z の成分を 1e-5 ～ 1e5 の範囲で正の変数に対数変換します。どの値が適切であるかがわからないので、広い範囲を選択します。

sigma = optimizableVariable('sigma',[1e-5,1e5],'Transform','log');
box = optimizableVariable('box',[1e-5,1e5],'Transform','log');

目的関数

この関数ハンドルは、[sigma,box] というパラメーターで交差検証損失を計算します。詳細については、kfoldLossを参照してください。

bayesopt は変数 z を 1 行のテーブルとして目的関数に渡します。

minfn = @(z)kfoldLoss(fitcsvm(cdata,grp,'CVPartition',c,...
    'KernelFunction','rbf','BoxConstraint',z.box,...
    'KernelScale',z.sigma));

分類器の最適化

bayesopt を使用して最良のパラメーター [sigma,box] を求めます。再現性を得るために、'expected-improvement-plus' の獲得関数を選択します。既定の獲得関数は実行時に決定されるので、結果が異なる場合があります。

results = bayesopt(minfn,[sigma,box],'IsObjectiveDeterministic',true,...
    'AcquisitionFunctionName','expected-improvement-plus')
|=====================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |        sigma |          box |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|    1 | Best   |        0.61 |     0.30468 |        0.61 |        0.61 |   0.00013375 |        13929 |
|    2 | Best   |       0.345 |     0.13733 |       0.345 |       0.345 |        24526 |        1.936 |
|    3 | Accept |        0.61 |     0.36218 |       0.345 |       0.345 |    0.0026459 |   0.00084929 |
|    4 | Accept |       0.345 |     0.36818 |       0.345 |       0.345 |       3506.3 |   6.7427e-05 |
|    5 | Accept |       0.345 |     0.27962 |       0.345 |       0.345 |       9135.2 |       571.87 |
|    6 | Accept |       0.345 |     0.21188 |       0.345 |       0.345 |        99701 |        10223 |
|    7 | Best   |       0.295 |     0.36377 |       0.295 |       0.295 |       455.88 |       9957.4 |
|    8 | Best   |        0.24 |      1.5955 |        0.24 |        0.24 |        31.56 |        99389 |
|    9 | Accept |        0.24 |       1.833 |        0.24 |        0.24 |       10.451 |        64429 |
|   10 | Accept |        0.35 |     0.23395 |        0.24 |        0.24 |       17.331 |   1.0264e-05 |
|   11 | Best   |        0.23 |      1.2786 |        0.23 |        0.23 |       16.005 |        90155 |
|   12 | Best   |         0.1 |     0.32002 |         0.1 |         0.1 |      0.36562 |        80878 |
|   13 | Accept |       0.115 |     0.19273 |         0.1 |         0.1 |       0.1793 |        68459 |
|   14 | Accept |       0.105 |     0.35092 |         0.1 |         0.1 |       0.2267 |        95421 |
|   15 | Best   |       0.095 |     0.20866 |       0.095 |       0.095 |      0.28999 |    0.0058227 |
|   16 | Best   |       0.075 |      0.3444 |       0.075 |       0.075 |      0.30554 |       8.9017 |
|   17 | Accept |       0.085 |     0.18246 |       0.075 |       0.075 |      0.41122 |       4.4476 |
|   18 | Accept |       0.085 |     0.33581 |       0.075 |       0.075 |      0.25565 |       7.8038 |
|   19 | Accept |       0.075 |     0.24164 |       0.075 |       0.075 |      0.32869 |       18.076 |
|   20 | Accept |       0.085 |     0.19534 |       0.075 |       0.075 |      0.32442 |       5.2118 |
|=====================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |        sigma |          box |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|   21 | Accept |         0.3 |     0.21495 |       0.075 |       0.075 |       1.3592 |    0.0098067 |
|   22 | Accept |        0.12 |     0.32474 |       0.075 |       0.075 |      0.17515 |   0.00070913 |
|   23 | Accept |       0.175 |     0.34526 |       0.075 |       0.075 |       0.1252 |     0.010749 |
|   24 | Accept |       0.105 |     0.32136 |       0.075 |       0.075 |       1.1664 |        31.13 |
|   25 | Accept |         0.1 |     0.35113 |       0.075 |       0.075 |      0.57465 |       2013.8 |
|   26 | Accept |        0.12 |     0.39497 |       0.075 |       0.075 |      0.42922 |   1.1602e-05 |
|   27 | Accept |        0.12 |     0.17536 |       0.075 |       0.075 |      0.42956 |   0.00027218 |
|   28 | Accept |       0.095 |     0.17675 |       0.075 |       0.075 |       0.4806 |       13.452 |
|   29 | Accept |       0.105 |     0.26193 |       0.075 |       0.075 |      0.19755 |       943.87 |
|   30 | Accept |       0.205 |     0.22987 |       0.075 |       0.075 |       3.5051 |       93.492 |

Figure contains an axes object. The axes object with title Objective function model, xlabel sigma, ylabel box contains 5 objects of type line, surface, contour. One or more of the lines displays its values using only markers These objects represent Observed points, Model mean, Next point, Model minimum feasible.

Figure contains an axes object. The axes object with title Min objective vs. Number of function evaluations, xlabel Function evaluations, ylabel Min objective contains 2 objects of type line. These objects represent Min observed objective, Estimated min objective.

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 43.9566 seconds
Total objective function evaluation time: 12.137

Best observed feasible point:
     sigma      box  
    _______    ______

    0.30554    8.9017

Observed objective function value = 0.075
Estimated objective function value = 0.075
Function evaluation time = 0.3444

Best estimated feasible point (according to models):
     sigma      box  
    _______    ______

    0.32869    18.076

Estimated objective function value = 0.075
Estimated function evaluation time = 0.25195

results = 
  BayesianOptimization with properties:

                      ObjectiveFcn: @(z)kfoldLoss(fitcsvm(cdata,grp,'CVPartition',c,'KernelFunction','rbf','BoxConstraint',z.box,'KernelScale',z.sigma))
              VariableDescriptions: [1x2 optimizableVariable]
                           Options: [1x1 struct]
                      MinObjective: 0.0750
                   XAtMinObjective: [1x2 table]
             MinEstimatedObjective: 0.0750
          XAtMinEstimatedObjective: [1x2 table]
           NumObjectiveEvaluations: 30
                  TotalElapsedTime: 43.9566
                         NextPoint: [1x2 table]
                            XTrace: [30x2 table]
                    ObjectiveTrace: [30x1 double]
                  ConstraintsTrace: []
                     UserDataTrace: {30x1 cell}
      ObjectiveEvaluationTimeTrace: [30x1 double]
                IterationTimeTrace: [30x1 double]
                        ErrorTrace: [30x1 double]
                  FeasibilityTrace: [30x1 logical]
       FeasibilityProbabilityTrace: [30x1 double]
               IndexOfMinimumTrace: [30x1 double]
             ObjectiveMinimumTrace: [30x1 double]
    EstimatedObjectiveMinimumTrace: [30x1 double]

XAtMinEstimatedObjective プロパティから、または関数 bestPoint を使用して、最適な推定実行可能点を取得します。既定では、関数 bestPoint は基準 'min-visited-upper-confidence-interval' を使用します。詳細については、bestPoint の名前と値の引数Criterionを参照してください。

results.XAtMinEstimatedObjective
ans=1×2 table
     sigma      box  
    _______    ______

    0.32869    18.076


z = bestPoint(results)
z=1×2 table
     sigma      box  
    _______    ______

    0.32869    18.076

最良の点を使用して、最適化された新しい SVM 分類器に学習させます。

SVMModel = fitcsvm(cdata,grp,'KernelFunction','rbf', ...
    'KernelScale',z.sigma,'BoxConstraint',z.box);

サポート ベクター分類器を可視化するため、グリッド全体でスコアを予測します。

d = 0.02;
[x1Grid,x2Grid] = meshgrid(min(cdata(:,1)):d:max(cdata(:,1)), ...
    min(cdata(:,2)):d:max(cdata(:,2)));
xGrid = [x1Grid(:),x2Grid(:)];
[~,scores] = predict(SVMModel,xGrid);

分類境界線をプロットします。

figure
h(1:2) = gscatter(cdata(:,1),cdata(:,2),grp,'rg','+*');
hold on
h(3) = plot(cdata(SVMModel.IsSupportVector,1) ,...
    cdata(SVMModel.IsSupportVector,2),'ko');
contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],'k');
legend(h,{'-1','+1','Support Vectors'},'Location','Southeast');

Figure contains an axes object. The axes object contains 4 objects of type line, contour. One or more of the lines displays its values using only markers These objects represent -1, +1, Support Vectors.

新しいデータにおける精度の評価

新しいテスト データ点を生成して分類します。

grnobj = gmdistribution(grnpop,.2*eye(2));
redobj = gmdistribution(redpop,.2*eye(2));

newData = random(grnobj,10);
newData = [newData;random(redobj,10)];
grpData = ones(20,1);  % green = 1
grpData(11:20) = -1; % red = -1

v = predict(SVMModel,newData);

テスト データ セットで誤分類率を計算します。

L = loss(SVMModel,newData,grpData)
L = 0.3500

正しく分類された新しいデータ点を確認します。正しく分類された点は赤い丸で囲まれ、正しく分類されていない点は黒い丸で囲まれています。

h(4:5) = gscatter(newData(:,1),newData(:,2),v,'mc','**');

mydiff = (v == grpData); % Classified correctly

for ii = mydiff % Plot red squares around correct pts
    h(6) = plot(newData(ii,1),newData(ii,2),'rs','MarkerSize',12);
end

for ii = not(mydiff) % Plot black squares around incorrect pts
    h(7) = plot(newData(ii,1),newData(ii,2),'ks','MarkerSize',12);
end
legend(h,{'-1 (training)','+1 (training)','Support Vectors', ...
    '-1 (classified)','+1 (classified)', ...
    'Correctly Classified','Misclassified'}, ...
    'Location','Southeast');
hold off

Figure contains an axes object. The axes object contains 8 objects of type line, contour. One or more of the lines displays its values using only markers These objects represent -1 (training), +1 (training), Support Vectors, -1 (classified), +1 (classified), Correctly Classified, Misclassified.

参考

|

関連するトピック