ベイズ最適化のプロット関数

組み込みプロット関数

2 組の組み込みプロット関数があります。

モデルプロット — D ≤ 2 の場合に適用	説明
`@plotAcquisitionFunction`	獲得関数の表面をプロットします。
`@plotConstraintModels`	各制約モデルの表面をプロットします。負の値は実行可能点を示します。 P (実行可能) 表面もプロットします。存在する場合は `–1` から `1` の範囲のエラーモデルもプロットします。負の値はモデルでエラーが発生する可能性が低いことを、正の値はエラーが発生する可能性が高いことを意味します。モデルは以下のようになります。 Plotted error = 2*Probability(error) – 1.
`@plotObjectiveEvaluationTimeModel`	目的関数の評価時間モデルの表面をプロットします。
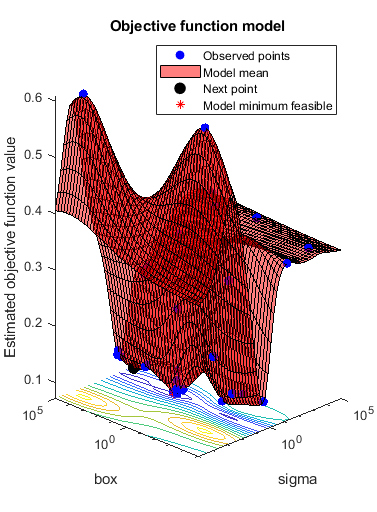
`@plotObjectiveModel`	`fun` モデルの表面、最小値の推定位置、および次に評価する予定になっている点の位置をプロットします。1 次元問題の場合、平均関数から 1 信頼区間分上下と平均から 1 ノイズ標準偏差分上下に包絡線をプロットします。

トレースプロット — すべての D に適用	説明
`@plotObjective`	観測された各関数値と関数評価の個数の関係をプロットします。
`@plotObjectiveEvaluationTime`	観測された各関数評価の実行時間と関数評価の個数の関係をプロットします。
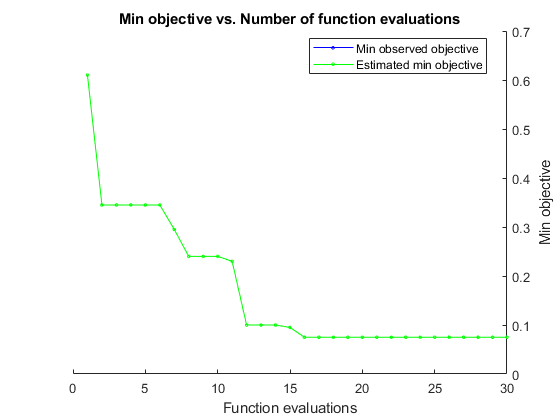
`@plotMinObjective`	観測および推定された最小の関数値と関数評価の個数の関係をプロットします。
`@plotElapsedTime`	最適化の合計経過時間、関数評価の合計時間、モデリングおよび点選択の合計時間という 3 つの曲線を関数評価の個数に対する関係としてプロットします。

メモ

連結制約がある場合、反復表示とプロット関数は次のような直観的ではない結果を与える可能性があります。

"最小目的" のプロットが増加する。
最適化において、以前に実行可能点が示された場合でも、問題が実行不可能であると宣言される場合がある。

このようになるのは、点が実行可能かどうかの判断が最適化の進行に応じて変化する可能性があるためです。bayesopt は制約モデルに関して実行可能性を判断しますが、このモデルは bayesopt が点を評価すると変化します。したがって、最小の点が後から実行不可能と判断された場合は "最小目的" プロットが増加し、反復表示には、後から実行不可能と判断される実行可能点が表示される可能性があります。

カスタムプロット関数の構文

カスタムプロット関数の構文はカスタム出力関数 (ベイズ最適化の出力関数を参照) と同じで、次のようになります:

stop = plotfun(results,state)

bayesopt は変数 results および state をカスタム関数に渡します。カスタム関数では、反復を停止する場合は true、継続する場合は false に設定した stop を返します。

results は、計算に関して使用できる情報が含まれている BayesianOptimization クラスのオブジェクトです。

state の取り得る値は次の 3 つです:

'initial' — bayesopt は反復を開始しようとしています。プロットの設定や他の初期化の実行にはこの状態を使用します。
'iteration' — bayesopt は反復を 1 回完了したところです。一般に、ほとんどのプロットや他の計算はこの状態で実行します。
'done' — bayesopt で最後の反復が完了しました。プロットをクリーンアップするか、プロット関数を停止する準備をします。

カスタムプロット関数の作成

スクリプトを開く

この例では、bayesopt のカスタムプロット関数を作成する方法を示します。さらに、BayesianOptimization オブジェクトの UserData プロパティに含まれている情報を使用する方法を示します。

問題の定義

問題は、交差検証損失を最小化するサポートベクターマシン (SVM) 分類のパラメーターを求めることです。具体的なモデルはbayesopt を使用した交差検証分類器の最適化の場合と同じです。したがって、目的関数は基本的に同じですが、UserData (このケースでは、現在のパラメーターに当てはめる SVM モデル内のサポートベクターの個数) も計算する点が異なります。

最適化の進行に応じて SVM モデル内のサポートベクターの個数をプロットするカスタムプロット関数を作成します。プロット関数でサポートベクターの個数にアクセスできるようにするため、サポートベクターの個数を返す 3 番目の出力 UserData を作成します。

目的関数

目的関数を作成します。この関数では、固定された交差検証分割に対する交差検証損失を計算し、生成されたモデル内のサポートベクターの個数を返します。

function [f,viol,nsupp] = mysvmminfn(x,cdata,grp,c)
SVMModel = fitcsvm(cdata,grp,'KernelFunction','rbf',...
    'KernelScale',x.sigma,'BoxConstraint',x.box);
f = kfoldLoss(crossval(SVMModel,'CVPartition',c));
viol = [];
nsupp = sum(SVMModel.IsSupportVector);
end

カスタムプロット関数

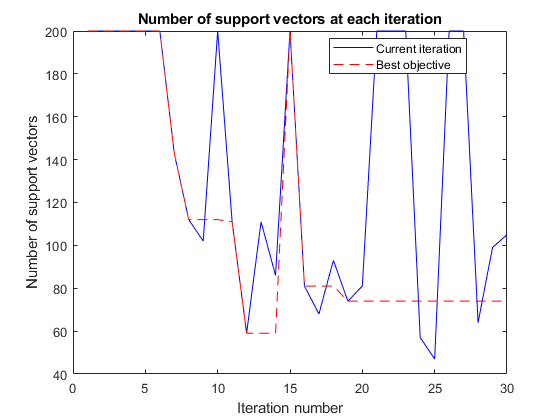
UserData で計算される情報を使用するカスタムプロット関数を作成します。現在の制約の個数と最良の目的関数が見つかった状態におけるモデルの制約の個数の両方を関数にプロットさせます。

function stop = svmsuppvec(results,state)
persistent hs nbest besthist nsupptrace
stop = false;
switch state
    case 'initial'
        hs = figure;
        besthist = [];
        nbest = 0;
        nsupptrace = [];
    case 'iteration'
        figure(hs)
        nsupp = results.UserDataTrace{end};   % get nsupp from UserDataTrace property.
        nsupptrace(end+1) = nsupp; % accumulate nsupp values in a vector.
        if (results.ObjectiveTrace(end) == min(results.ObjectiveTrace)) || (length(results.ObjectiveTrace) == 1) % current is best
            nbest = nsupp;
        end
        besthist = [besthist,nbest];
        plot(1:length(nsupptrace),nsupptrace,'b',1:length(besthist),besthist,'r--')
        xlabel 'Iteration number'
        ylabel 'Number of support vectors'
        title 'Number of support vectors at each iteration'
        legend('Current iteration','Best objective','Location','best')
        drawnow
end

モデルの設定

各クラスについて 10 個ずつの基底点を生成します。

rng default
grnpop = mvnrnd([1,0],eye(2),10);
redpop = mvnrnd([0,1],eye(2),10);

各クラスについて 100 個ずつのデータ点を生成します。

redpts = zeros(100,2);grnpts = redpts;
for i = 1:100
    grnpts(i,:) = mvnrnd(grnpop(randi(10),:),eye(2)*0.02);
    redpts(i,:) = mvnrnd(redpop(randi(10),:),eye(2)*0.02);
end

データを 1 つの行列に格納し、各点のクラスにラベルを付けるベクトル grp を作成します。

cdata = [grnpts;redpts];
grp = ones(200,1);
% Green label 1, red label -1
grp(101:200) = -1;

既定の SVM パラメーターを使用して、すべてのデータの基本分類をチェックします。

SVMModel = fitcsvm(cdata,grp,'KernelFunction','rbf','ClassNames',[-1 1]);

交差検証を固定する分割を設定します。この手順を行わないと、交差検証がランダムになるので、目的関数が確定的ではなくなります。

c = cvpartition(200,'KFold',10);

元の当てはめたモデルの交差検証の精度をチェックします。

loss = kfoldLoss(fitcsvm(cdata,grp,'CVPartition',c,...
    'KernelFunction','rbf','BoxConstraint',SVMModel.BoxConstraints(1),...
    'KernelScale',SVMModel.KernelParameters.Scale))

loss =

    0.1350

最適化用の変数の準備

目的関数は、入力 z = [rbf_sigma,boxconstraint] を受け入れ、交差検証損失値 z を返します。z の成分を 1e-5 ～ 1e5 の範囲で正の変数に対数変換します。どの値が適切であるかがわからないので、広い範囲を選択します。

sigma = optimizableVariable('sigma',[1e-5,1e5],'Transform','log');
box = optimizableVariable('box',[1e-5,1e5],'Transform','log');

プロット関数の設定とオプティマイザーの呼び出し

bayesopt を使用して最良のパラメーター [sigma,box] を求めます。再現性を得るために、'expected-improvement-plus' の獲得関数を選択します。既定の獲得関数は実行時に決定されるので、結果が異なる場合があります。

反復回数の関数としてサポートベクターの個数をプロットし、見つかった最良のパラメーターに対するサポートベクターの個数をプロットします。

obj = @(x)mysvmminfn(x,cdata,grp,c);
results = bayesopt(obj,[sigma,box],...
    'IsObjectiveDeterministic',true,'Verbose',0,...
    'AcquisitionFunctionName','expected-improvement-plus',...
    'PlotFcn',{@svmsuppvec,@plotObjectiveModel,@plotMinObjective})

results = 

  BayesianOptimization with properties:

                      ObjectiveFcn: @(x)mysvmminfn(x,cdata,grp,c)
              VariableDescriptions: [1x2 optimizableVariable]
                           Options: [1x1 struct]
                      MinObjective: 0.0750
                   XAtMinObjective: [1x2 table]
             MinEstimatedObjective: 0.0750
          XAtMinEstimatedObjective: [1x2 table]
           NumObjectiveEvaluations: 30
                  TotalElapsedTime: 57.4489
                         NextPoint: [1x2 table]
                            XTrace: [30x2 table]
                    ObjectiveTrace: [30x1 double]
                  ConstraintsTrace: []
                     UserDataTrace: {30x1 cell}
      ObjectiveEvaluationTimeTrace: [30x1 double]
                IterationTimeTrace: [30x1 double]
                        ErrorTrace: [30x1 double]
                  FeasibilityTrace: [30x1 logical]
       FeasibilityProbabilityTrace: [30x1 double]
               IndexOfMinimumTrace: [30x1 double]
             ObjectiveMinimumTrace: [30x1 double]
    EstimatedObjectiveMinimumTrace: [30x1 double]