振動信号の包絡線スペクトルの計算

信号アナライザーを使用して、ベアリング振動信号の包絡線スペクトルを計算して欠陥を調査します。MATLAB® スクリプトと関数を生成して、解析を自動化します。

ベアリング振動データの生成

図に示す大きさをもつベアリングは、1 秒あたり $f_{0} = 25$ 回駆動されます。加速度計はベアリングの振動を 10 kHz でサンプリングします。

例の最後の関数 bearingdata を使用して、2 つの欠陥ベアリングから振動信号を生成します。信号の 1 つ xBPFO で、ベアリングの外輪に欠陥があります。その他の信号 xBPFI では、ベアリングの内輪に欠陥があります。ベアリングのモデリングと欠陥の診断の詳細については、回転機の振動解析とenvspectrumを参照してください。

[t,xBPFO,xBPFI,bpfi] = bearingdata;

信号アナライザーを使用した包絡線スペクトルの計算

信号アナライザーを開いて BPFO 信号をディスプレイにドラッグします。信号テーブルでそれを選択し、[アナライザー] タブで [時間値] をクリックすることで、信号に時間情報を追加します。Sample Rate and Start Time を選択して、サンプルレートに 10 kHz を入力します。

[表示] タブで、[スペクトル] をクリックしてスペクトルビューを開きます。振動信号のスペクトルは、bearingdata で指定された 3 kHz の影響を及ぼす周波数によって変調された BPFO 高調波を示します。スペクトルの下端では、駆動周波数とその次数により、その他の特徴が不明確になります。

信号を選択し、[アナライザー] タブで、[複製] をクリックしてコピーを生成します。新しい信号に名前 envspec を指定して、ディスプレイにドラッグします。ヒルベルト変換を使用して、信号の包絡線スペクトルを計算します。信号テーブル内の envspec を選択し、[前処理] をクリックして前処理モードを開始します。

信号の DC 値を削除します。[関数] ギャラリーで、[トレンド除去] を選択します。[関数パラメーター] パネルで、Constant をトレンド除去手法として選択します。[適用] をクリックします。
トレンド除去された信号をバンドパスフィルター処理します。[関数] ギャラリーで、[バンドパス] を選択します。[関数パラメーター] パネルで、低域および高域通過帯域周波数としてそれぞれ 2250 Hz と 3750 Hz を入力します。[適用] をクリックします。
フィルター処理された信号の包絡線を計算します。[関数] ギャラリーで、[包絡線] を選択します。[関数パラメーター] パネルで、Hilbert を方法として選択します。[適用] をクリックします。
包絡線の DC 値を削除します。[関数] ギャラリーで、[トレンド除去] を選択します。[関数パラメーター] パネルで、Constant をトレンド除去手法として選択します。[適用] をクリックします。

[情報] 列のアイコンをクリックして、前処理情報を表示します。

[すべて確定] をクリックして前処理結果を保存し、モードを終了します。包絡線スペクトルがディスプレイのスペクトルビューに表示されます。包絡線スペクトルによって BPFO 高調波が明瞭に表示されます。

統合された解析スクリプトを作成するためのステップ

包絡線スペクトルの計算を多数の異なるベアリングに対して繰り返さなければならない場合、単調で時間がかかる作業になります。信号アナライザーは、計算を自動化できる MATLAB® スクリプトと関数を生成できます。

演習として、BPFI 信号に対する前の解析を繰り返します。信号アナライザーは、次のような自動化に役立つ 2 つのコンポーネントを生成します。

preprocess: トレンド除去、フィルター処理、包絡線の計算によって信号を前処理する関数
Compute power spectrum: 包絡線スペクトルを計算するスクリプト

統合された解析スクリプトを作成するには、変更されていない前処理関数とプロットスクリプトの両方を単一ファイルに入れます (または、個別のファイルに関数を保存できます)。

単一の MATLAB® スクリプトにスクリプトと関数を保存する場合、関数が最後に表示されなければならないことに注意してください。
各関数の最後にキーワード end を追加しなければなりません。

1.前処理関数の作成

最初に、前処理ステップを再現する関数を作成します。envspec 信号を選択します。[アナライザー] タブの [関数の生成] をクリックします。既定で preprocess と呼ばれる関数がエディターに表示されます。統合された解析スクリプトの最後に生成された関数を保存します。関数は、時間情報を指定する 2 番目の引数を予測します。関数を使用して BPFI 信号を前処理します。

envspec = preprocess(xBPFI,t);

2.スペクトルスクリプトの作成

アプリで、名前の隣にあるチェックボックスをオフにして、ディスプレイから未処理の信号を削除します。[表示] タブの [スクリプトの生成] をクリックして、Spectrum Script を選択します。スクリプトがエディターで開きます。統合された解析スクリプトに生成したコードを含めます。解析スクリプトを実行すると、生成したスペクトルスクリプトは、前処理した BPFI 信号の包絡線スペクトルを計算します。

% Compute power spectrum

% Generated by MATLAB(R) 9.6 and Signal Processing Toolbox 8.2.
% Generated on: 12-Nov-2018 15:13:34

% Parameters
timeLimits = [0 0.9999]; % seconds
frequencyLimits = [0 5000]; % Hz

%%
% Index into signal time region of interest
envspec_ROI = envspec(:);
sampleRate = 10000; % Hz
startTime = 0; % seconds
minIdx = ceil(max((timeLimits(1)-startTime)*sampleRate,0))+1;
maxIdx = floor(min((timeLimits(2)-startTime)*sampleRate,length(envspec_ROI)-1))+1;
envspec_ROI = envspec_ROI(minIdx:maxIdx);

% Compute spectral estimate
% Run the function call below without output arguments to plot the results
[Penvspec_ROI, Fenvspec_ROI] = pspectrum(envspec_ROI,sampleRate, ...
    FrequencyLimits=frequencyLimits);

3.包絡線スペクトルのプロット

包絡線スペクトルをプロットします。ピークの位置と最初の 10 個の BPFI の高調波の周波数を比較します。出力引数のない pspectrum コマンドを使用して包絡線スペクトルをプロットすることもできます。

plot(Fenvspec_ROI,(Penvspec_ROI))
xline((1:10)*bpfi,":")
xlim([0 10*bpfi])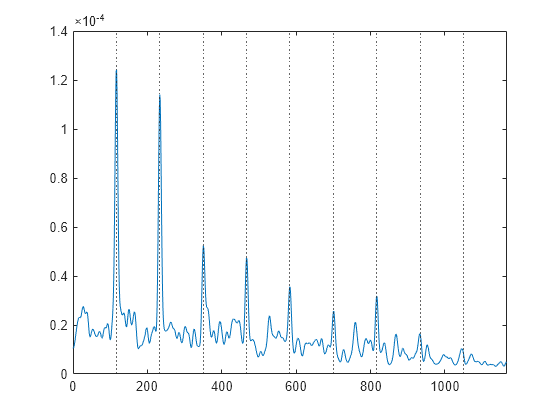

関数コード

単一の前処理関数

アプリによって生成された信号前処理関数は、トレンド除去、バンドパスフィルター処理、および包絡線計算を組み合わせます。

function y = preprocess(x,tx)
%  Preprocess input x
%    This function expects an input vector x and a vector of time values
%    tx. tx is a numeric vector in units of seconds.

% Generated by MATLAB(R) 9.6 and Signal Processing Toolbox 8.2.
% Generated on: 12-Nov-2018 15:09:44

y = detrend(x,"constant");
Fs = 1/mean(diff(tx)); % Average sample rate
y = bandpass(y,[2250 3750],Fs,Steepness=0.85,StopbandAttenuation=60);
[y,~] = envelope(y);
y = detrend(y,"constant");
end

関数を生成するベアリングデータ

ベアリングのピッチの直径は、 $p = 12$ cm で、ベアリングの接触角は $θ = 0$ です。各 $n = 8$ 回転要素の直径は $d = 2$ cm です。内輪が 1 秒あたり $f_{0} = 25$ 回駆動される間、外輪は静止状態を保ちます。加速度計はベアリングの振動を 10 kHz でサンプリングします。

function [t,xBPFO,xBPFI,bpfi] = bearingdata

p = 0.12;
d = 0.02;
n = 8;
th = 0;
f0 = 25;
fs = 10000;

正常なベアリングの場合、振動信号は、ホワイトガウスノイズに組み込まれている、駆動周波数の複数の次数の重ね合わせです。

t = 0:1/fs:1-1/fs;
z = [1 0.5 0.2 0.1 0.05]*sin(2*pi*f0*[1 2 3 4 5]'.*t);

xHealthy = z + randn(size(z))/10;

外輪に欠陥があると、時間の経過と共にベアリングの摩耗を引き起す 5 ミリ秒の一連の影響の原因となります。影響は、ベアリングの外輪転動体通過周波数 (BPFO: Ball Pass Frequency Outer race) で発生します。

$BPFO = \frac{1}{2} {nf}_{0} [1 - \frac{d}{p} \cos θ]$ .

影響を指数関数的に減衰する 3 kHz の正弦波の周期列としてモデル化します。BPFO 振動信号を生成するために正常な信号に影響を追加します。

bpfo = n*f0/2*(1-d/p*cos(th));

tmp = 0:1/fs:5e-3-1/fs;
xmp = sin(2*pi*3000*tmp).*exp(-1000*tmp);

xBPFO = xHealthy + pulstran(t,0:1/bpfo:1,xmp,fs)/4;

代わりに、内輪に欠陥がある場合、影響が次の周波数で発生します。

$BPFI = \frac{1}{2} {nf}_{0} [1 + \frac{d}{p} \cos θ]$ .

正常な信号に影響を追加して BPFI 振動信号を生成します。

bpfi = n*f0/2*(1+d/p*cos(th));

xBPFI = xHealthy + pulstran(t,0:1/bpfi:1,xmp,fs)/4;

end

振動信号の包絡線スペクトルの計算

ベアリング振動データの生成

信号アナライザーを使用した包絡線スペクトルの計算

統合された解析スクリプトを作成するためのステップ

関数コード

参考

アプリ

関数

関連する例

詳細