envspectrum
機械診断の包絡線スペクトル
構文
説明
es = envspectrum(___,Name=Value)
出力引数を設定せずに envspectrum(___) を使用すると、現在の Figure に包絡線信号と包絡線スペクトルがプロットされます。
例
2 つの振動信号、健全なベアリングの信号と破損したベアリングの信号をシミュレーションします。これらの包絡線スペクトルを計算して比較します。
ピッチの直径が 12 cm のベアリングは 8 つの回転要素を持ちます。各回転要素の直径は 2 cm です。内輪が 1 秒あたり 25 回駆動される間、外輪は静止状態を保ちます。加速度計はベアリングの振動を 10 kHz でサンプリングします。
fs = 10000; f0 = 25; n = 8; d = 0.02; p = 0.12;
健全なベアリングの振動信号には、駆動点周波数の次数が複数含まれます。0.1 秒分のデータをプロットします。
t = 0:1/fs:1-1/fs;
z = [1 0.5 0.2 0.1 0.05] ...
*sin(2*pi*f0*[1 2 3 4 5]'.*t)/5;
plot(t,z)
xlim([0.4 0.5])
ベアリングの外輪に欠陥があると、ベアリングで 5 ミリ秒の一連の影響を引き起こします。いずれ、これらの影響はベアリングの摩耗につながります。影響は、ベアリングの外輪転動体通過周波数 (BPFO: Ball Pass Frequency Outer race) で発生します。
ここで、 は駆動レート、n は回転要素の数、d は回転要素の直径、p はベアリングのピッチの直径、θ はベアリングの接触角です。接触角は 0 と仮定して BPFO を計算します。
ca = 0; bpfo = n*f0/2*(1-d/p*cos(ca))
bpfo = 83.3333
フラット トップ ウィンドウによってウィンドウ処理された 3 kHz 正弦波の周期列として衝撃をモデル化します。0.1 秒分のデータをプロットします。
fImpact = 3000;
tImpact = 0:1/fs:5e-3-1/fs;
xImpact = sin(2*pi*fImpact*tImpact)...
.*flattopwin(length(tImpact))'/10;
x = pulstran(t,0:1/bpfo:t(end),xImpact,fs)/3;
plot(t,x+z)
xlim([0.4 0.5])
ホワイト ガウス ノイズを信号に付加します。1/30² のノイズ分散を指定します。0.1 秒分のデータをプロットします。
yGood = z + randn(size(z))/30; yBad = x+z + randn(size(z))/30; plot(t,yGood,t,yBad) xlim([0.4 0.5]) legend("Healthy","Damaged")
包絡線信号とスペクトルを計算してプロットします。
envspectrum([yGood' yBad'],fs) xlim([0 10*bpfo]/1000)
ピークの位置と BPFO の高調波の周波数を比較します。包絡線スペクトルの BPFO 高調波は、ベアリング摩耗の兆候です。
harmImpact = (1:10)*bpfo; xline(harmImpact/1000,":") legend("Healthy","Damaged","BPFO harmonics")
信号のウェルチ スペクトルを計算します。5 Hz の周波数分解能を指定します。
figure pspectrum([yGood' yBad'],fs,FrequencyResolution=5) legend("Healthy","Damaged")
スペクトルの下端では、駆動周波数とその次数により、その他の特徴が不明確になります。異常がないベアリングのスペクトルと破損したベアリングのスペクトルは、区別できません。
xlim([0 10*bpfo]/1000)
故障したベアリングのスペクトルは、影響を及ぼす周波数によって変調された BPFO 高調波を示します。
xlim((bpfo*[-10 10]+fImpact)/1000)
10 ミリ秒ごとに 1 回転するベアリングの振動信号に似た 2 チャネル信号を生成します。信号は 10 kHz で 0.2 秒間サンプリングされます。これはベアリングの 20 回転に相当します。
fs = 10000; tmax = 20; mlt = 0.01; t = 0:1/fs:mlt-1/fs;
各 10 ミリ秒間隔の間に:
最初のチャネルは減衰定数が 700、正弦波周波数が 600 Hz の減衰正弦波です。
2 番目のチャネルは減衰定数が 800、正弦波周波数が 500 Hz の別の減衰正弦波です。2 番目のチャネルは最初のチャネルから 5 ミリ秒遅れています。
信号をプロットします。
y1 = sin(2*pi*600*t).*exp(-700*t); y2 = sin(2*pi*500*t).*exp(-800*t); y2 = [y2(51:100) y2(1:50)]; T = (0:1/fs:mlt*tmax-1/fs)'; Y = repmat([y1;y2],1,tmax)'; plot(T,Y)
時間間隔 T を使用して duration 配列を作成します。この duration 配列と 2 チャネル信号で timetable を構築します。
dt = seconds(T); ttb = timetable(dt,Y);
出力引数を設定せずに envspectrum を使用して、2 つのチャネルの包絡線信号と包絡線スペクトルを表示します。最後の 100 Hz 間隔を除くナイキスト区間全体のスペクトルを計算します。
envspectrum(ttb,'Band',[100 4900])
信号の包絡線スペクトルには、反復レート 1/0.01 = 0.1 kHz の整数倍の位置にピークがあります。これは予測とまったく同じです。envspectrum は、高周波数の正弦波成分を除去し、低周波数の反復動作に注目します。包絡線スペクトルが回転機の解析に役立つツールであるのは、このためです。
包絡線信号とその計算回数を計算します。出力変数の型を確認します。
[~,~,ttbenv,ttbt] = envspectrum(ttb,'Band',[100 4900]); whos ttb*
Name Size Bytes Class Attributes ttb 2000x1 48977 timetable ttbenv 2000x1 48985 timetable ttbt 2000x1 16002 duration
時間ベクトルの型は、入力 timetable の時間値のような、duration です。出力 timetable のサイズは、入力 timetable と同じです。
入力 timetable の各チャネルを、別々の変数として保存します。包絡線信号と時間ベクトルを計算します。出力の型を確認します。
btb = timetable(dt,Y(:,1),Y(:,2)); [~,~,btbenv,btbt] = envspectrum(btb,'Band',[100 4900]); whos btb*
Name Size Bytes Class Attributes btb 2000x2 49231 timetable btbenv 2000x2 49251 timetable btbt 2000x1 16002 duration
出力 timetable のサイズは、入力 timetable と同じです。
1 kHz で 5 秒間サンプリングされた信号を生成します。信号は、T = 0.25 秒ごとに繰り返される 0.01 秒の矩形パルスで構成されています。搬送周波数 150 Hz の正弦波で信号の振幅変調を行います。
fs = 1e3; tmax = 5; t = 0:1/fs:tmax; y = pulstran(t,0:0.25:tmax,rectpuls=0.01); fc = 150; z = modulate(y,fc,fs);
元の信号と変調した信号をプロットします。最初の数サイクルのみを表示します。
plot(t,y,t,z,"-") grid on axis([0 1 -1.1 1.1])
信号の包絡線と包絡線スペクトルを計算します。複素数復調を使用して信号の包絡線を決定します。搬送周波数を中心として 20 Hz 間隔で包絡線スペクトルを計算します。
[q,f,e,te] = envspectrum(z,fs,Method="demod",Band=[fc-10 fc+10]);包絡線信号と包絡線スペクトルをプロットします。0 から 50 Hz の区間を拡大します。
subplot(2,1,1) plot(te,e) xlabel("Time") title("Envelope") subplot(2,1,2) plot(f,q) xlim([0 50]) xlabel("Frequency") title("Envelope Spectrum")
包絡線信号の周期 T = 0.25 秒は、元の信号と同じです。包絡線スペクトルのパルスは 1 / T = 4 Hz です。
計算を繰り返しますが、今度は関数 hilbert を使用して包絡線を計算します。10 次有限インパルス応答 (FIR) フィルターを使用して信号をバンドパス フィルター処理します。組み込み関数 envspectrum を使用して包絡線信号と包絡線スペクトルをプロットします。
envspectrum(z,fs,Method="hilbert",FilterOrder=10)
分散 1/3 のホワイト ガウス ノイズに信号を組み込みます。結果をプロットします。
zn = z + randn(size(z))/3; plot(t,zn,"-") grid on axis([0 1 -1.1 1.1])
包絡線信号と包絡線スペクトルを計算して表示します。搬送周波数を中心として 10 Hz 間隔で、複素数復調を使用して包絡線スペクトルを計算します。0 から 50 Hz の区間を拡大します。
envspectrum(zn,fs,Band=[fc-5 fc+5]) xlim([0 50])
入力引数
名前と値の引数
出力引数
アルゴリズム
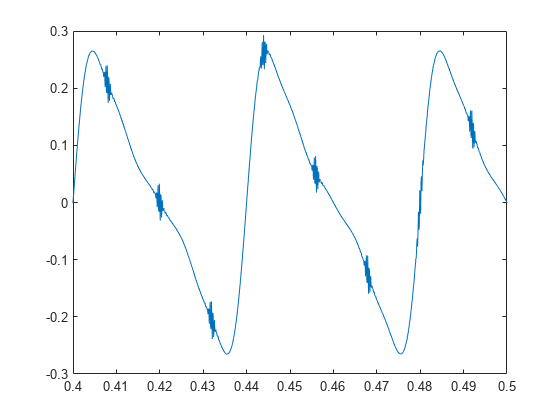
envspectrum は、最初に入力信号 x から DC バイアスを取り除き、包絡線信号を計算します。
Methodを"hilbert"に設定した場合、関数は次の処理を行います。信号をバンドパス フィルター処理します。FIR フィルターの次数は
FilterOrderと、ba(1)およびba(2)のカットオフ周波数で指定されます。ここでbaはBandを使用して指定される周波数帯域です。関数
hilbertを使用して解析信号を計算します。包絡線信号を解析信号の絶対値として計算します。
Methodを"demod"に設定した場合、関数は次の処理を行います。信号の複素数復調を実行します。信号は、exp(j2πf0t) で乗算されます。ここで、f0 = (
ba(1)+ba(2))/2 です。復調した信号をローパス フィルター処理し、解析信号を計算します。FIR フィルターの次数は、
FilterOrderと、(ba(2)–ba(1))/2 のカットオフ周波数で指定されます。包絡線信号を解析信号の絶対値の 2 倍として計算します。
関数は、包絡線信号の計算後、包絡線から DC バイアスを取り除き、FFT を使用して包絡線スペクトルを計算します。
参照
[1] Randall, Robert Bond. Vibration-Based Condition Monitoring. Chichester, UK: John Wiley & Sons, 2011.
