fitrlinear

高次元データに対する線形回帰モデルの当てはめ

構文

Mdl = fitrlinear(X,Y)

Mdl = fitrlinear(Tbl,ResponseVarName)

Mdl = fitrlinear(Tbl,formula)

Mdl = fitrlinear(Tbl,Y)

Mdl = fitrlinear(X,Y,Name,Value)

[Mdl,FitInfo] = fitrlinear(___)

[Mdl,FitInfo,HyperparameterOptimizationResults] = fitrlinear(___)

説明

fitrlinear は、高次元の非スパースまたはスパース予測子データを使用して効率的に線形回帰モデルに学習をさせます。使用可能な線形回帰モデルには、正則化されたサポート ベクター マシン (SVM) と最小二乗回帰法があります。fitrlinear は、計算時間を短縮する手法 (確率的勾配降下法など) を使用して目的関数を最小化します。

多数の予測子変数が含まれている高次元データセットに対する計算時間を短縮するには、fitrlinear を使用して線形回帰モデルに学習をさせます。低～中次元の予測子データセットについては、低次元データの代替方法を参照してください。

Mdl = fitrlinear(X,Y) は、サポート ベクター マシン回帰モデルを予測子 X および応答 Y に当てはめた結果が格納されている、学習済みの回帰モデル オブジェクト Mdl を返します。

Mdl = fitrlinear(Tbl,ResponseVarName) は、テーブル Tbl 内の予測子変数と Tbl.ResponseVarName 内の応答値を使用して、線形回帰モデルを返します。

Mdl = fitrlinear(Tbl,formula) は、テーブル Tbl 内の標本データを使用して、線形回帰モデルを返します。入力引数 formula は、Mdl を当てはめるために使用する Tbl 内の予測子変数の応答およびサブセットの説明モデルです。

Mdl = fitrlinear(Tbl,Y) は、テーブル Tbl 内の予測子変数とベクトル Y 内の応答値を使用して、線形回帰モデルを返します。

Mdl = fitrlinear(X,Y,Name,Value) では、前の構文におけるいずれかの入力引数の組み合わせに加えて、1 つ以上の名前と値のペアの引数を使用してオプションを指定します。たとえば、交差検証の指定、最小二乗回帰の実装、正則化のタイプの指定が可能です。名前と値のペアの引数 'Kfold' を使用して交差検証を行うことをお勧めします。交差検証の結果により、モデルがどの程度一般化を行うかを判断します。

[Mdl,FitInfo] = fitrlinear(___) は、前の構文のいずれかを使用して、最適化の詳細も返します。交差検証済みモデルについて FitInfo を要求することはできません。

[Mdl,FitInfo,HyperparameterOptimizationResults] = fitrlinear(___) は、名前と値のペア OptimizeHyperparameters が渡された場合に、ハイパーパラメーターの最適化の詳細も返します。

例

線形回帰モデルの学習

SVM、双対 SGD およびリッジ正則化を使用して線形回帰モデルに学習をさせます。

次のモデルにより、10000 個の観測値をシミュレートします。

$$y=x_{100}+2x_{200}+e.$$

• $$X=x_1,...,x_{1000}$$ は、10% の要素が非ゼロ標準正規である 10000 行 1000 列のスパース行列です。

• e は、平均が 0、標準偏差が 0.3 のランダムな正規誤差です。

rng(1) % For reproducibility
n = 1e4;
d = 1e3;
nz = 0.1;
X = sprandn(n,d,nz);
Y = X(:,100) + 2*X(:,200) + 0.3*randn(n,1);

線形回帰モデルに学習をさせます。既定の設定では、fitrlinear はリッジ ペナルティがあるサポート ベクター マシンを使用し、SVM 用の双対 SGD を使用して最適化を行います。近似の要約を抽出して、最適化アルゴリズムによるモデルがどの程度データに当てはまるかを判断します。

[Mdl,FitInfo] = fitrlinear(X,Y)

Mdl = 
  RegressionLinear
         ResponseName: 'Y'
    ResponseTransform: 'none'
                 Beta: [1000x1 double]
                 Bias: -0.0056
               Lambda: 1.0000e-04
              Learner: 'svm'


  Properties, Methods

FitInfo = struct with fields:
                    Lambda: 1.0000e-04
                 Objective: 0.2725
                 PassLimit: 10
                 NumPasses: 10
                BatchLimit: []
             NumIterations: 100000
              GradientNorm: NaN
         GradientTolerance: 0
      RelativeChangeInBeta: 0.4907
             BetaTolerance: 1.0000e-04
             DeltaGradient: 1.5816
    DeltaGradientTolerance: 0.1000
           TerminationCode: 0
         TerminationStatus: {'Iteration limit exceeded.'}
                     Alpha: [10000x1 double]
                   History: []
                   FitTime: 0.0452
                    Solver: {'dual'}

Mdl は RegressionLinear モデルです。Mdl と学習データまたは新しいデータを loss に渡して、標本内平均二乗誤差を調べることができます。または、Mdl と新しい予測子データを predict に渡して、新しい観測値の応答を予測することができます。

FitInfo は、重要な情報として終了ステータス (TerminationStatus) とソルバーによるモデルのデータへの当てはめにかかった時間 (FitTime) が含まれている構造体配列です。FitInfo を使用して、最適化終了時の結果が満足できるものであるかどうかを判断することをお勧めします。この場合、fitrlinear は最大反復回数に達しました。モデルに再学習をさせることもできますが、学習時間は短いので、データを通す回数を増やしてください。または、LBFGS など別のソルバーを試してください。

交差検証の使用による適切な LASSO ペナルティの特定

最小二乗を使用する線形回帰モデルに適した LASSO ペナルティの強度を決定するため、5 分割の交差検証を実装します。

次のモデルにより、10000 個の観測値をシミュレートします。

$$y=x_{100}+2x_{200}+e.$$

• $$X=\{x_1,...,x_{1000}\}$$ は、10% の要素が非ゼロ標準正規である 10000 行 1000 列のスパース行列です。

• e は、平均が 0、標準偏差が 0.3 のランダムな正規誤差です。

rng(1) % For reproducibility
n = 1e4;
d = 1e3;
nz = 0.1;
X = sprandn(n,d,nz);
Y = X(:,100) + 2*X(:,200) + 0.3*randn(n,1);

$$10^{-5}$$ ～ $$10^{-1}$$ の範囲で対数間隔で配置された 15 個の正則化強度を作成します。

Lambda = logspace(-5,-1,15);

モデルを交差検証します。実行速度を向上させるため、予測子データを転置し、観測値が列単位であることを指定します。SpaRSA を使用して目的関数を最適化します。

X = X'; 
CVMdl = fitrlinear(X,Y,'ObservationsIn','columns','KFold',5,'Lambda',Lambda,...
    'Learner','leastsquares','Solver','sparsa','Regularization','lasso');

numCLModels = numel(CVMdl.Trained)

numCLModels = 5

CVMdl は RegressionPartitionedLinear モデルです。fitrlinear は 5 分割の交差検証を実装するので、各分割について学習させる 5 つの RegressionLinear モデルが CVMdl に格納されます。

1 番目の学習済み線形回帰モデルを表示します。

Mdl1 = CVMdl.Trained{1}

Mdl1 = 
  RegressionLinear
         ResponseName: 'Y'
    ResponseTransform: 'none'
                 Beta: [1000x15 double]
                 Bias: [-0.0049 -0.0049 -0.0049 -0.0049 -0.0049 -0.0048 ... ]
               Lambda: [1.0000e-05 1.9307e-05 3.7276e-05 7.1969e-05 ... ]
              Learner: 'leastsquares'


  Properties, Methods

Mdl1 は RegressionLinear モデル オブジェクトです。fitrlinear は最初の 4 つの分割に対して学習を行うことにより Mdl1 を構築しました。Lambda は正則化強度のシーケンスなので、Mdl1 はそれぞれが Lambda の各正則化強度に対応する 15 個のモデルであると考えることができます。

交差検証された MSE を推定します。

mse = kfoldLoss(CVMdl);

Lambda の値が大きくなると、予測子変数がスパースになります。これは回帰モデルの品質として優れています。データセット全体を使用し、モデルの交差検証を行ったときと同じオプションを指定して、各正則化強度について線形回帰モデルに学習をさせます。モデルごとに非ゼロの係数を特定します。

Mdl = fitrlinear(X,Y,'ObservationsIn','columns','Lambda',Lambda,...
    'Learner','leastsquares','Solver','sparsa','Regularization','lasso');
numNZCoeff = sum(Mdl.Beta~=0);

同じ図に、各正則化強度についての交差検証された MSE と非ゼロ係数の頻度をプロットします。すべての変数を対数スケールでプロットします。

figure
[h,hL1,hL2] = plotyy(log10(Lambda),log10(mse),...
    log10(Lambda),log10(numNZCoeff)); 
hL1.Marker = 'o';
hL2.Marker = 'o';
ylabel(h(1),'log_{10} MSE')
ylabel(h(2),'log_{10} nonzero-coefficient frequency')
xlabel('log_{10} Lambda')
hold off

予測子変数のスパース性と MSE の低さのバランスがとれている正則化強度 (Lambda(10) など) のインデックスを選択します。

idxFinal = 10;

最小の MSE に対応するモデルを抽出します。

MdlFinal = selectModels(Mdl,idxFinal)

MdlFinal = 
  RegressionLinear
         ResponseName: 'Y'
    ResponseTransform: 'none'
                 Beta: [1000x1 double]
                 Bias: -0.0050
               Lambda: 0.0037
              Learner: 'leastsquares'


  Properties, Methods

idxNZCoeff = find(MdlFinal.Beta~=0)

idxNZCoeff = 2×1

   100
   200

EstCoeff = Mdl.Beta(idxNZCoeff)

EstCoeff = 2×1

    1.0051
    1.9965

MdlFinal は、1 つの正則化強度がある RegressionLinear モデルです。非ゼロ係数 EstCoeff は、データをシミュレートした係数に近くなっています。

線形回帰の最適化

この例では、fitrlinear を使用して自動的にハイパーパラメーターを最適化する方法を示します。この例では、人為的な (シミュレートされた) データをモデルに対して使用します。

$$y=x_{100}+2x_{200}+e.$$

• $$X=\{x_1,...,x_{1000}\}$$ は、10% の要素が非ゼロ標準正規である 10000 行 1000 列のスパース行列です。

• e は、平均が 0、標準偏差が 0.3 のランダムな正規誤差です。

rng(1) % For reproducibility
n = 1e4;
d = 1e3;
nz = 0.1;
X = sprandn(n,d,nz);
Y = X(:,100) + 2*X(:,200) + 0.3*randn(n,1);

自動的なハイパーパラメーター最適化を使用して、5 分割交差検証損失を最小化するハイパーパラメーターを求めます。

再現性を得るために、'expected-improvement-plus' の獲得関数を使用します。

hyperopts = struct('AcquisitionFunctionName','expected-improvement-plus');
[Mdl,FitInfo,HyperparameterOptimizationResults] = fitrlinear(X,Y,...
    'OptimizeHyperparameters','auto',...
    'HyperparameterOptimizationOptions',hyperopts)

|=====================================================================================================|
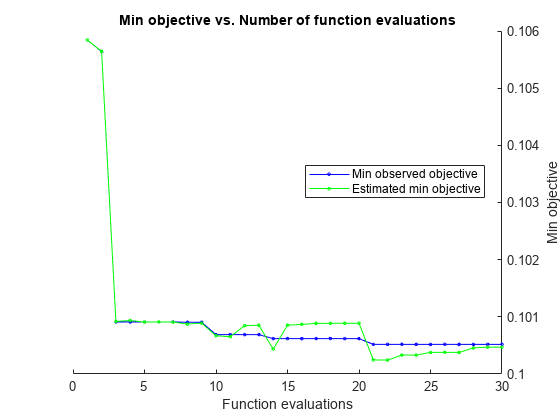
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |       Lambda |      Learner |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|    1 | Best   |     0.10584 |     0.90217 |     0.10584 |     0.10584 |   2.4206e-09 |          svm |
|    2 | Best   |     0.10558 |      0.5725 |     0.10558 |      0.1057 |     0.001807 |          svm |
|    3 | Best   |     0.10091 |     0.38784 |     0.10091 |     0.10092 |   2.4681e-09 | leastsquares |
|    4 | Accept |     0.11397 |     0.30297 |     0.10091 |     0.10095 |     0.021027 | leastsquares |
|    5 | Best   |     0.10091 |     0.36937 |     0.10091 |     0.10091 |   2.9697e-09 | leastsquares |
|    6 | Accept |     0.45312 |     0.50525 |     0.10091 |     0.10091 |       9.8803 |          svm |
|    7 | Accept |     0.10578 |     0.89213 |     0.10091 |     0.10091 |   9.6873e-06 |          svm |
|    8 | Best   |      0.1009 |     0.40921 |      0.1009 |     0.10087 |   1.7286e-05 | leastsquares |
|    9 | Accept |     0.44998 |     0.41223 |      0.1009 |     0.10089 |       9.9615 | leastsquares |
|   10 | Best   |     0.10068 |      0.5657 |     0.10068 |     0.10066 |   0.00081737 | leastsquares |
|   11 | Accept |     0.10582 |      1.2577 |     0.10068 |     0.10065 |   9.7512e-08 |          svm |
|   12 | Accept |     0.10091 |      0.3682 |     0.10068 |     0.10084 |   3.4449e-07 | leastsquares |
|   13 | Accept |     0.10575 |      1.1579 |     0.10068 |     0.10085 |   0.00019667 |          svm |
|   14 | Best   |     0.10063 |     0.41455 |     0.10063 |     0.10044 |    0.0038216 | leastsquares |
|   15 | Accept |     0.10091 |     0.32001 |     0.10063 |     0.10086 |   2.7403e-08 | leastsquares |
|   16 | Accept |     0.10091 |     0.33962 |     0.10063 |     0.10088 |   1.0017e-09 | leastsquares |
|   17 | Accept |     0.10091 |     0.34277 |     0.10063 |     0.10089 |   2.6319e-06 | leastsquares |
|   18 | Accept |     0.10584 |     0.67124 |     0.10063 |     0.10089 |   1.0049e-09 |          svm |
|   19 | Accept |     0.10087 |     0.30682 |     0.10063 |     0.10089 |   0.00010789 | leastsquares |
|   20 | Accept |     0.10578 |      0.7737 |     0.10063 |     0.10089 |   1.0008e-06 |          svm |
|=====================================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |       Lambda |      Learner |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|   21 | Best   |     0.10052 |      0.3429 |     0.10052 |     0.10024 |    0.0021701 | leastsquares |
|   22 | Accept |     0.10091 |     0.39173 |     0.10052 |     0.10024 |   9.8207e-08 | leastsquares |
|   23 | Accept |     0.10052 |     0.33319 |     0.10052 |     0.10033 |    0.0021352 | leastsquares |
|   24 | Accept |     0.10091 |     0.36783 |     0.10052 |     0.10033 |   9.8774e-09 | leastsquares |
|   25 | Accept |     0.10052 |     0.24667 |     0.10052 |     0.10038 |    0.0021099 | leastsquares |
|   26 | Accept |     0.10091 |     0.28391 |     0.10052 |     0.10038 |    9.351e-07 | leastsquares |
|   27 | Accept |     0.31614 |     0.66163 |     0.10052 |     0.10045 |      0.16873 |          svm |
|   28 | Accept |      0.1057 |     0.67995 |     0.10052 |     0.10047 |   0.00071833 |          svm |
|   29 | Accept |     0.10081 |     0.27742 |     0.10052 |     0.10047 |   0.00030307 | leastsquares |
|   30 | Accept |     0.10091 |     0.37112 |     0.10052 |     0.10047 |   6.6735e-06 | leastsquares |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 31.3839 seconds
Total objective function evaluation time: 15.2282

Best observed feasible point:
     Lambda        Learner   
    _________    ____________

    0.0021701    leastsquares

Observed objective function value = 0.10052
Estimated objective function value = 0.10047
Function evaluation time = 0.3429

Best estimated feasible point (according to models):
     Lambda        Learner   
    _________    ____________

    0.0021701    leastsquares

Estimated objective function value = 0.10047
Estimated function evaluation time = 0.35063

Mdl = 
  RegressionLinear
         ResponseName: 'Y'
    ResponseTransform: 'none'
                 Beta: [1000x1 double]
                 Bias: -0.0071
               Lambda: 0.0022
              Learner: 'leastsquares'


  Properties, Methods

FitInfo = struct with fields:
                    Lambda: 0.0022
                 Objective: 0.0473
            IterationLimit: 1000
             NumIterations: 15
              GradientNorm: 2.4329e-06
         GradientTolerance: 1.0000e-06
      RelativeChangeInBeta: 3.3727e-05
             BetaTolerance: 1.0000e-04
             DeltaGradient: []
    DeltaGradientTolerance: []
           TerminationCode: 1
         TerminationStatus: {'Tolerance on coefficients satisfied.'}
                   History: []
                   FitTime: 0.1002
                    Solver: {'lbfgs'}

HyperparameterOptimizationResults = 
  BayesianOptimization with properties:

                      ObjectiveFcn: @createObjFcn/inMemoryObjFcn
              VariableDescriptions: [3x1 optimizableVariable]
                           Options: [1x1 struct]
                      MinObjective: 0.1005
                   XAtMinObjective: [1x2 table]
             MinEstimatedObjective: 0.1005
          XAtMinEstimatedObjective: [1x2 table]
           NumObjectiveEvaluations: 30
                  TotalElapsedTime: 31.3839
                         NextPoint: [1x2 table]
                            XTrace: [30x2 table]
                    ObjectiveTrace: [30x1 double]
                  ConstraintsTrace: []
                     UserDataTrace: {30x1 cell}
      ObjectiveEvaluationTimeTrace: [30x1 double]
                IterationTimeTrace: [30x1 double]
                        ErrorTrace: [30x1 double]
                  FeasibilityTrace: [30x1 logical]
       FeasibilityProbabilityTrace: [30x1 double]
               IndexOfMinimumTrace: [30x1 double]
             ObjectiveMinimumTrace: [30x1 double]
    EstimatedObjectiveMinimumTrace: [30x1 double]

この最適化手法は交差検証の使用による適切な LASSO ペナルティの特定で示されているものよりシンプルですが、モデルの複雑度と交差検証損失との間のトレードオフはできません。

入力引数

X — 予測子データ

非スパース行列 | スパース行列

予測子データ。n 行 p 列の非スパース行列またはスパース行列を指定します。

Y の長さと X の観測値数は同じでなければなりません。

メモ

観測値が列に対応するように予測子行列を配置して 'ObservationsIn','columns' を指定すると、最適化実行時間が大幅に短縮される可能性があります。

データ型: single | double

Y — 応答データ

数値ベクトル

応答データ。n 次元の数値ベクトルを指定します。Y の長さは X または Tbl の観測値の数と等しくなければなりません。

データ型: single | double

Tbl — 標本データ

テーブル

モデルを学習させるために使用する標本データ。テーブルとして指定します。Tbl の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。オプションとして、Tbl に応答変数用の列を 1 つ追加できます。文字ベクトルの cell 配列ではない cell 配列と複数列の変数は使用できません。

• Tbl に応答変数が含まれている場合に Tbl 内の他の変数をすべて予測子として使用するには、ResponseVarName を使用して応答変数を指定します。

• Tbl に応答変数が含まれている場合に Tbl 内の他の変数の一部のみを予測子として使用するには、formula を使用して式を指定します。

• Tbl に応答変数が含まれていない場合は、Y を使用して応答変数を指定します。応答変数の長さと Tbl の行数は等しくなければなりません。

ResponseVarName — 応答変数名

Tbl 内の変数の名前

応答変数の名前。Tbl 内の変数の名前で指定します。応答変数は、数値ベクトルでなければなりません。

ResponseVarName には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、応答変数 Y が Tbl に Tbl.Y として格納されている場合、'Y' を指定します。それ以外の場合、モデルを学習させるときに、Tbl の列は Y を含めてすべて予測子として扱われます。

データ型: char | string

formula — 応答変数および予測子変数サブセットの説明モデル

文字ベクトル | string スカラー

応答変数および予測子変数サブセットの説明モデル。"Y~x1+x2+x3" という形式の文字ベクトルまたは string スカラーを指定します。この形式では、Y は応答変数を、x1、x2 および x3 は予測子変数を表します。

モデルに学習をさせるための予測子として Tbl 内の変数のサブセットを指定するには、式を使用します。式を指定した場合、formula に現れない Tbl 内の変数は使用されません。

式の変数名は Tbl の変数名 (Tbl.Properties.VariableNames) であり、有効な MATLAB^® 識別子でなければなりません。関数 isvarname を使用して Tbl の変数名を検証できます。変数名が有効でない場合、関数 matlab.lang.makeValidName を使用してそれらを変換できます。

データ型: char | string

メモ:

ソフトウェアは、NaN、空の文字ベクトル ('')、空の string ("")、<missing>、および <undefined> の要素を欠損値として扱い、以下のいずれかの特性をもつ観測値を削除します。

• 応答の欠損値 (たとえば、Y または ValidationData{2})

• 予測子の観測値 (たとえば、X または ValidationData{1} の行) 内の少なくとも 1 つの欠損値

• NaN 値または重み 0 (たとえば、Weights または ValidationData{3} 内の値)

メモリを節約するため、学習を行う前に欠損値が含まれている観測値を学習データから手動で削除することをお勧めします。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後ろにする必要がありますが、ペアの順序は関係ありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: Mdl = fitrlinear(X,Y,'Learner','leastsquares','CrossVal','on','Regularization','lasso') は、最小二乗回帰の実装、10 分割交差検証の実装、および LASSO 正則化項を含めることを指定します。

メモ

交差検証の名前と値の引数は、名前と値の引数 'OptimizeHyperparameters' と一緒には使用できません。'OptimizeHyperparameters' の場合の交差検証は、名前と値の引数 'HyperparameterOptimizationOptions' を使用することのみによって変更できます。

線形回帰のオプション

Epsilon — イプシロン不感応区間の幅の半分

iqr(Y)/13.49 (既定値) | 非負のスカラー値

イプシロン不感応区間の幅の半分。'Epsilon' と非負のスカラー値から構成されるコンマ区切りのペアとして指定します。'Epsilon' は SVM 学習器のみに適用されます。

Epsilon の既定値は、iqr(Y)/13.49 です。これは、応答変数 Y の四分位数間範囲を使用した標準偏差の推定値です。iqr(Y) がゼロに等しい場合、Epsilon の既定値は 0.1 になります。

例: 'Epsilon',0.3

データ型: single | double

Lambda — 正則化項の強度

'auto' (既定値) | 非負のスカラー | 非負値のベクトル。

正則化項の強度。'Lambda' と 'auto'、非負のスカラーまたは非負値のベクトルから構成されるコンマ区切りのペアとして指定します。

• 'auto' の場合、Lambda = 1/n です。

  • 交差検証の名前と値のペアの引数 (CrossVal など) を指定した場合、n は分割内観測値の数です。

  • それ以外の場合、n は学習標本のサイズです。

• 非負値のベクトルの場合、fitrlinear は、Lambda の異なる値それぞれについて目的関数の最適化を逐次的に昇順で実行します。

  • Solver が 'sgd' または 'asgd' で Regularization が 'lasso' の場合、fitrlinear が前の係数の推定値を次の最適化反復のウォーム スタートとして使用することはありません。それ以外の場合、fitrlinear はウォーム スタートを使用します。

  • Regularization が 'lasso' の場合、fitrlinear が Lambda の以後の値を使用して最適化を行うときに、係数の推定値 0 は値が保持されます。

  • fitrlinear は、指定された正則化強度ごとに係数の推定値を返します。

例: 'Lambda',10.^(-(10:-2:2))

データ型: char | string | double | single

Learner — 線形回帰モデルのタイプ

'svm' (既定値) | 'leastsquares'

線形回帰モデルのタイプ。'Learner' と 'svm' または 'leastsquares' から構成されるコンマ区切りのペアとして指定します。

次の表では、$$f\left(x\right)=x\beta +b.$$ です。

• β は p 個の係数のベクトルです。

• x は p 個の予測子変数による観測値です。

• b はスカラー バイアスです。

値	アルゴリズム	応答の範囲	損失関数
'leastsquares'	通常の最小二乗による線形回帰	y ∊ (-∞,∞)	平均二乗誤差 (MSE): $$\ell \left[y,f\left(x\right)\right]=\frac{1}{2}{\left[y-f\left(x\right)\right]}^2$$
'svm'	サポート ベクター マシン回帰	'leastsquares' と同じ	イプシロン不感応: $$\ell \left[y,f\left(x\right)\right]=\max \left[0,\left|y-f\left(x\right)\right|-\epsilon \right]$$

例: 'Learner','leastsquares'

ObservationsIn — 予測子データにおける観測値の次元

'rows' (既定値) | 'columns'

予測子データにおける観測値の次元。'rows' または 'columns' として指定します。

メモ

観測値が列に対応するように予測子行列を配置して 'ObservationsIn','columns' を指定すると、計算時間が大幅に短縮される可能性があります。table の予測子データに対して 'ObservationsIn','columns' を指定することはできません。

例: 'ObservationsIn','columns'

データ型: char | string

Regularization — 複雑度ペナルティのタイプ

'lasso' | 'ridge'

複雑度ペナルティのタイプ。'Regularization' と 'lasso' または 'ridge' から構成されるコンマ区切りのペアとして指定します。

最小化のための目的関数は、平均損失関数 (Learner を参照) と次の表の正則化項を加算することにより作成されます。

値	説明
'lasso'	LASSO (L1) ペナルティ: $$\lambda {\displaystyle \sum _{j=1}^p\left|{\beta }_j\right|}$$
'ridge'	リッジ (L2) ペナルティ: $$\frac{\lambda }{2}{\displaystyle \sum _{j=1}^p{\beta }_j^2}$$

正則化項の強度 (式の λ) を指定するには、Lambda を使用します。

バイアス項 (β₀) は正則化ペナルティから除外されます。

Solver が 'sparsa' の場合、Regularization の既定値は 'lasso' になります。それ以外の場合は、既定値は 'ridge' です。

ヒント

• 予測子変数を選択する場合は、'lasso' を指定します。変数の選択の詳細については、特徴選択の紹介を参照してください。

• 最適化の精度を向上させるには、'ridge' を指定します。

例: 'Regularization','lasso'

Solver — 目的関数の最小化手法

'sgd' | 'asgd' | 'dual' | 'bfgs' | 'lbfgs' | 'sparsa' | string 配列 | 文字ベクトルの cell 配列

目的関数の最小化手法。'Solver' と次の表の値をもつ文字ベクトル、string スカラー、string 配列、または文字ベクトルの cell 配列から構成されるコンマ区切りのペアとして指定します。

値	説明	制限
'sgd'	確率的勾配降下法 (SGD) [5][3]
'asgd'	平均化確率的勾配降下法 (ASGD) [8]
'dual'	SVM 用の双対 SGD [2][7]	Regularization は 'ridge'、Learner は 'svm' でなければなりません。
'bfgs'	Broyden-Fletcher-Goldfarb-Shanno 準ニュートン アルゴリズム (BFGS) [4]	X の次元数が非常に多い場合は非効率的です。
'lbfgs'	記憶制限 BFGS (LBFGS) [4]	Regularization は 'ridge' でなければなりません。
'sparsa'	可分近似によるスパース再構成 (SpaRSA) [6]	Regularization は 'lasso' でなければなりません。

指定する項目によって、内容は次のように変わります。

• size(X,1) <= 100 (予測子変数が 100 個以下) の場合にリッジ ペナルティ (Regularization を参照) を指定すると、既定のソルバーは 'bfgs' になります。

• size(X,1) > 100 (予測子変数が 100 個超) の場合に SVM 回帰モデル (Learner を参照) とリッジ ペナルティを指定すると、既定のソルバーは 'dual' になります。

• X に 100 個以下の予測子変数が格納されている場合に LASSO ペナルティを指定すると、既定のソルバーは 'sparsa' になります。

それ以外の場合、既定のソルバーは 'sgd' になります。既定のソルバーはハイパーパラメーターの最適化を実行するときに変更できることに注意してください。詳細については、ハイパーパラメーターの最適化で使用されるソルバーを正則化手法に基づいて決定を参照してください。

ソルバー名の string 配列または cell 配列を指定する場合、Lambda のそれぞれの値に対して、ソルバー j の解がソルバー j + 1 のウォーム スタートとして使用されます。

例: {'sgd' 'lbfgs'} は、オブジェクティブを解決するために SGD を適用し、解を LBFGS のウォーム スタートとして使用します。

ヒント

• SGD および ASGD は他のソルバーより高速に目的関数を解決できるのに対し、LBFGS および SpaRSA は他のソルバーより正確な解が得られます。{'sgd' 'lbfgs'} や {'sgd' 'sparsa'} のようにソルバーを組み合わせると、速度と精度の最適化のバランスをとることができます。

• SGD と ASGD のいずれかを選択する場合、以下を考慮します。

  • SGD は反復あたりの時間が短くなりますが、収束するまでに必要な反復回数が多くなります。

  • ASGD は収束するまでに必要な反復回数が少なくなりますが、反復あたりの時間が長くなります。

• 予測子データが高次元で Regularization が 'ridge' の場合、Solver に次の組み合わせのいずれかを設定します。

  • 'sgd'

  • 'asgd'

  • 'dual' (Learner が 'svm' の場合)

  • 'lbfgs'

  • {'sgd','lbfgs'}

  • {'asgd','lbfgs'}

  • {'dual','lbfgs'} (Learner が 'svm' の場合)

  他の組み合わせも設定できますが、多くの場合、不十分な精度の解となります。

• 予測子データが中～低次元で Regularization が 'ridge' の場合、Solver を 'bfgs' に設定します。

• Regularization が 'lasso' の場合、Solver に次の組み合わせのいずれかを設定します。

  • 'sgd'

  • 'asgd'

  • 'sparsa'

  • {'sgd','sparsa'}

  • {'asgd','sparsa'}

例: 'Solver',{'sgd','lbfgs'}

Beta — 線形係数の初期推定値

zeros(p,1) (既定値) | 数値ベクトル | 数値行列

線形係数の初期推定値 (β)、'Beta' と p 次元の数値ベクトルまたは p 行 L 列の数値行列から構成されるコンマ区切りのペアとして指定します。p は X の予測子変数の数、L は正則化強度値の数です (詳細については、Lambda を参照)。

• p 次元ベクトルを指定した場合、次のプロセスを使用して目的関数が L 回最適化されます。

  1. 初期値として Beta、正則化強度として Lambda の最小値を使用して最適化を行う。

  2. 前回の最適化で生成された推定値をウォーム スタートとして使用し、Lambda 内の次に小さい値を正則化強度として使用して、再度最適化を行う。

  3. Lambda の値をすべて使用するまでステップ 2 を繰り返す。

• p 行 L 列の行列を指定した場合、目的関数が L 回最適化されます。反復 j では、初期値として Beta(:,j) が使用され、Lambda を昇順で並べ替えた後で正則化強度として Lambda(j) が使用されます。

'Solver','dual' を設定した場合、Beta は無視されます。

データ型: single | double

Bias — 切片の初期推定値

数値スカラー | 数値ベクトル

切片の初期推定値 (b)。'Bias' と数値スカラーまたは L 次元の数値ベクトルから構成されるコンマ区切りのペアとして指定します。L は正則化強度値の数です (詳細については、Lambda を参照)。

• スカラーを指定した場合、次のプロセスを使用して目的関数が L 回最適化されます。

  1. 初期値として Bias、正則化強度として Lambda の最小値を使用して最適化を行う。

  2. 生成された推定値を次回の最適化の反復でウォーム スタートとして使用し、Lambda 内の次に小さい値を正則化強度として使用する。

  3. Lambda の値をすべて使用するまでステップ 2 を繰り返す。

• L 次元ベクトルを指定した場合、目的関数が L 回最適化されます。反復 j では、初期値として Bias(j) が使用され、Lambda を昇順で並べ替えた後で正則化強度として Lambda(j) が使用されます。

• 既定の設定では、次のようになります。

  • Learner が 'leastsquares' の場合、Bias は学習の場合は Y の、交差検証の場合は分割内応答の加重平均になります。

  • Learner が 'svm' の場合、Bias は学習の場合はすべての学習についての Y の、交差検証の場合は Epsilon より大きい分割内観測値の加重中央値になります。

データ型: single | double

FitBias — 線形モデルの切片使用フラグ

true (既定値) | false

線形モデルの切片使用フラグ。'FitBias' と true または false から構成されるコンマ区切りのペアとして指定します。

値	説明
true	線形モデルにバイアス項 b が追加され、推定されます。
false	推定時に b = 0 に設定されます。

例: 'FitBias',false

データ型: logical

PostFitBias — 最適化後に線形モデルの切片を当てはめるフラグ

false (既定値) | true

最適化後に線形モデルの切片を当てはめるフラグ。'PostFitBias' と true または false から構成されるコンマ区切りのペアとして指定します。

値	説明
false	最適化時にバイアス項 b と係数 β が推定されます。
true	b を推定するため、以下が行われます。 モデルを使用して β と b を推定する。 残差を計算する。 b を再度当てはめる。最小二乗の場合、b は残差の加重平均です。SVM 回帰の場合、b は大きさが Epsilon より大きいすべての残差の加重中央値です。

true を指定する場合、FitBias は true でなければなりません。

例: 'PostFitBias',true

データ型: logical

Verbose — 詳細レベル

0 (既定値) | 非負の整数

詳細レベル。'Verbose' と非負の整数から構成されるコンマ区切りのペアとして指定します。Verbose は、fitrlinear がコマンド ラインに表示する診断情報の量を制御します。

値	説明
0	fitrlinear は診断情報を表示しません。
1	fitrlinear は、目的関数の値や勾配の大きさなどの診断情報を定期的に表示および格納します。診断情報は FitInfo.History に格納されます。
他の正の整数	fitrlinear は、各最適化反復における診断情報を表示および格納します。診断情報は FitInfo.History に格納されます。

例: 'Verbose',1

データ型: double | single

SGD および ASGD ソルバーのオプション

BatchSize — ミニバッチのサイズ

正の整数

ミニバッチのサイズ。'BatchSize' と正の整数から構成されるコンマ区切りのペアとして指定します。各反復では、学習データの観測値を BatchSize 個使用して劣勾配が推定されます。

• X が数値行列の場合、既定値は 10 です。

• X がスパース行列の場合、既定値は max([10,ceil(sqrt(ff))]) です。ここで、ff = numel(X)/nnz(X) (X の "スパース性係数") です。

例: 'BatchSize',100

データ型: single | double

LearnRate — 学習率

正のスカラー

学習率。'LearnRate' と正のスカラーから構成されるコンマ区切りのペアとして指定します。LearnRate では、各反復で実行するステップの回数を指定します。各反復では、各ステップの方向と大きさが勾配により指定されます。

• Regularization が 'ridge' の場合、LearnRate は初期学習率 γ₀ を指定します。反復 t の学習率 γ_t は、次の式を使用して決定されます。

  $${\gamma }_t=\frac{{\gamma }_0}{{\left(1+\lambda {\gamma }_{0}t\right)}^c}.$$

  • λ は Lambda の値です。

  • Solver が 'sgd' の場合、c = 1 です。

  • Solver が 'asgd' の場合、次のようになります。

    • Learner が 'leastsquares' の場合は c = 2/3

    • Learner が 'svm' の場合は c = 3/4 [8]

• Regularization が 'lasso' の場合、すべての反復について LearnRate は一定になります。

既定の設定では、LearnRate は 1/sqrt(1+max((sum(X.^2,obsDim)))) です。obsDim は、観測値が X の列である場合は 1、それ以外の場合は 2 です。

例: 'LearnRate',0.01

データ型: single | double

OptimizeLearnRate — 学習率を減少させるフラグ

true (既定値) | false

発散 (最小値の限度を超える状態) が検出された場合に学習率を減少させるフラグ。'OptimizeLearnRate' と true または false から構成されるコンマ区切りのペアとして指定します。

OptimizeLearnRate が 'true' の場合、次のようになります。

1. 数回の最適化反復について、LearnRate を学習率として使用して最適化が開始される。

2. 目的関数の値が増加した場合、現在の学習率の半分の値を使用して再開される。

3. 目的関数が減少するまで、ステップ 2 が繰り返される。

例: 'OptimizeLearnRate',true

データ型: logical

TruncationPeriod — LASSO 切り捨て実行間のミニバッチの回数

10 (既定値) | 正の整数

LASSO 切り捨て実行間のミニバッチの回数。'TruncationPeriod' と正の整数から構成されるコンマ区切りのペアとして指定します。

切り捨て実行の後で、ソフトしきい値が線形係数に適用されます。つまり、k = TruncationPeriod 回のミニバッチが処理された後で、次を使用して係数推定 j が切り捨てられます。

$${\widehat{\beta }}_j^{\ast }=\{\begin{array}{ll}{\widehat{\beta }}_j-u_t\hfill & \text{if}{\widehat{\beta }}_j>u_t,\hfill \\ 0\hfill & \text{if}\left|{\widehat{\beta }}_j\right|\le u_t,\hfill \\ {\widehat{\beta }}_j+u_t\hfill & \text{if}{\widehat{\beta }}_j<-u_t.\hfill \end{array}\begin{array}{r}\hfill \\ \hfill \\ \hfill \end{array}$$

• SGD の場合、$${\widehat{\beta }}_j$$ はミニバッチを次を満たす k の回数処理した後の係数 j の推定値です。$$u_t=k{\gamma }_t\lambda .$$γ_t は反復 t における学習率です。λ は Lambda の値です。

• ASGD の場合、$${\widehat{\beta }}_j$$ はミニバッチを次を満たす k の回数処理した後の係数 j の平均推定値です。$$u_t=k\lambda .$$

Regularization が 'ridge' の場合、TruncationPeriod は無視されます。

例: 'TruncationPeriod',100

データ型: single | double

他の回帰のオプション

CategoricalPredictors — カテゴリカル予測子のリスト

正の整数のベクトル | logical ベクトル | 文字行列 | string 配列 | 文字ベクトルの cell 配列 | 'all'

カテゴリカル予測子のリスト。次の表のいずれかの値として指定します。説明は、予測子データの行に観測値、列に予測子があると仮定しています。

値	説明
正の整数のベクトル	ベクトルの各エントリは、対応する予測子がカテゴリカルであることを示すインデックス値です。インデックス値の範囲は 1 ～ p です。p はモデルの学習に使用した予測子の数です。 fitrlinear が入力変数のサブセットを予測子として使用する場合、関数はサブセットのみを使用して予測子にインデックスを作成します。応答変数、観測値の重みの変数、および関数で使用されないその他の変数は、CategoricalPredictors 値でカウントされません。
logical ベクトル	true というエントリは、対応する予測子がカテゴリカルであることを意味します。ベクトルの長さは p です。
文字行列	行列の各行は予測子変数の名前です。名前は PredictorNames のエントリに一致しなくてはなりません。文字行列の各行が同じ長さになるように、名前を余分な空白で埋めてください。
文字ベクトルの cell 配列または string 配列	配列の各要素は予測子変数の名前です。名前は PredictorNames のエントリに一致しなくてはなりません。
"all"	すべての予測子がカテゴリカルです。

既定では、予測子データがテーブル (Tbl) 内にある場合、fitrlinear は、その変数が logical ベクトル、categorical ベクトル、文字配列、string 配列または文字ベクトルの cell 配列のいずれかである場合に、変数を categorical であると見なします。予測子データが行列 (X) である場合、fitrlinear はすべての予測子が連続的であると見なします。他の予測子をカテゴリカル予測子として指定するには、名前と値の引数 CategoricalPredictors を使用してそれらを指定します。

特定されたカテゴリカル予測子に対して、fitrlinear はカテゴリカル変数に順序が設定されていないか順序が設定されているかに応じて、2 つの異なる方式を使用してダミー変数を作成します。順序付けのないカテゴリカル変数の場合、fitrlinear は、そのカテゴリカル変数の各レベルについて 1 つずつダミー変数を作成します。順序付けされたカテゴリカル変数の場合、fitrlinear は、カテゴリの数よりも 1 つ少ないダミー変数を作成します。詳細については、ダミー変数の自動作成を参照してください。

例: 'CategoricalPredictors','all'

データ型: single | double | logical | char | string | cell

PredictorNames — 予測子変数名

一意な名前の string 配列 | 一意な文字ベクトルの cell 配列

予測子変数名。一意な名前の string 配列または一意な文字ベクトルの cell 配列として指定します。'PredictorNames' の機能は、学習データの提供方法によって決まります。

• X と Y を指定した場合、'PredictorNames' を使用して X 内の予測子変数に名前を割り当てることができます。

  • PredictorNames 内の名前の順序は、X の予測子の順序に一致しなければなりません。X が既定の方向 (行に観測値、列に予測子) をもつと仮定すると、PredictorNames{1} は X(:,1) の名前、PredictorNames{2} は X(:,2) の名前 (以下同様) になります。また、size(X,2) と numel(PredictorNames) は等しくなければなりません。

  • 既定では PredictorNames は {'x1','x2',...} です。

• Tbl が与えられた場合、'PredictorNames' を使用して学習に使用する予測子変数を選択できます。つまり、fitrlinear は、学習中に PredictorNames の予測子変数と応答変数のみを使用します。

  • PredictorNames は Tbl.Properties.VariableNames のサブセットでなければならず、応答変数の名前を含めることはできません。

  • 既定では、すべての予測子変数の名前が PredictorNames に格納されます。

  • 'PredictorNames' と formula の両方ではなく、いずれか一方を使用して学習用の予測子を指定することをお勧めします。

例: 'PredictorNames',{'SepalLength','SepalWidth','PetalLength','PetalWidth'}

データ型: string | cell

ResponseName — 応答変数名

"Y" (既定値) | 文字ベクトル | string スカラー

応答変数名。文字ベクトルまたは string スカラーとして指定します。

• Y を指定した場合、ResponseName を使用して応答変数の名前を指定できます。

• ResponseVarName または formula を指定した場合、ResponseName を使用できません。

例: "ResponseName","response"

データ型: char | string

ResponseTransform — 応答の変換

'none' (既定値) | 関数ハンドル

応答の変換。'none' または関数ハンドルのいずれかとして指定します。既定の設定は 'none' です。これは @(y)y、つまり変換なしを表します。MATLAB 関数またはユーザー定義関数の場合は、応答変換用の関数ハンドルを使用します。関数ハンドルは、ベクトル (元の応答値) を受け入れて同じサイズのベクトル (変換した応答値) を返さなければなりません。

例: myfunction = @(y)exp(y) を使用して、指数変換を入力ベクトルに適用する関数のハンドルを作成するとします。この場合、応答変換として 'ResponseTransform',myfunction を指定できます。

データ型: char | string | function_handle

Weights — 観測値の重み

正の数値ベクトル | Tbl 内の変数の名前

観測値の重み。'Weights' と、正の数値ベクトル (または Tbl に含まれる変数の名前) から構成されるコンマ区切りのペアとして指定します。ソフトウェアは、X または Tbl の各観測値に、Weights の対応する値で重みを付けます。Weights の長さは、X または Tbl の観測値の数と等しくなければなりません。

入力データをテーブル Tbl として指定した場合、Weights は数値ベクトルが含まれている Tbl 内の変数の名前にすることができます。この場合、Weights には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、重みのベクトル W が Tbl.W として格納されている場合、'W' として指定します。それ以外の場合、モデルを学習させるときに、Tbl の列は W を含めてすべて予測子として扱われます。

既定の設定では、Weights は ones(n,1) です。n は X または Tbl の観測値数です。

fitrlinear は合計が 1 になるように重みを正規化します。

データ型: single | double | char | string

交差検証オプション

CrossVal — 交差検証フラグ

'off' (既定値) | 'on'

交差検証フラグ。'Crossval' と 'on' または 'off' から構成されるコンマ区切りのペアとして指定します。

'on' を指定した場合、10 分割の交差検証が実施されます。

この交差検証の設定をオーバーライドするには、名前と値のペアの引数 CVPartition、Holdout、KFold のいずれかを使用します。交差検証済みモデルを作成するために使用できる交差検証の名前と値のペアの引数は、一度に 1 つだけです。

例: 'Crossval','on'

CVPartition — 交差検証分割

[] (既定値) | cvpartition 分割オブジェクト

交差検証分割。'CVPartition' と cvpartition により作成された cvpartition 分割オブジェクトで構成されるコンマ区切りのペアとして指定します。分割オブジェクトは交差検証のタイプおよび学習と検証セットのインデックス付けを指定します。

交差検証済みモデルを作成するために使用できるオプションは、'CVPartition'、'Holdout'、'KFold' のいずれかのみです。

Holdout — ホールドアウト検証の対象データの比率

(0,1) の範囲のスカラー値

ホールドアウト検証に使用されるデータの比率。'Holdout' と、(0,1) の範囲内のスカラー値から成るコンマ区切りのペアとして指定します。'Holdout',p を指定すると、次が実行されます。

1. p*100% のデータを検証データとして無作為に予約し、残りのデータを使用してモデルを学習させる

2. コンパクトな学習済みモデルを交差検証済みモデルの Trained プロパティに格納する。

交差検証済みモデルを作成するために使用できるオプションは、'CVPartition'、'Holdout'、'KFold' のいずれかのみです。

例: 'Holdout',0.1

データ型: double | single

KFold — 分割の数

10 (既定値) | 1 より大きい正の整数値

交差検証分類器で使用する分割の数。'KFold' と 1 より大きい正の整数値から構成されるコンマ区切りのペアとして指定します。たとえば 'KFold',k を指定すると、次が実行されます。

1. データを無作為に k 個のセットに分割する

2. 各セットについて、そのセットを検証データとして予約し、他の k – 1 個のセットを使用してモデルに学習をさせる

3. k 個のコンパクトな学習済みモデルを、交差検証済みモデルの Trained プロパティに含まれている k 行 1 列の cell ベクトルのセルに格納する。

交差検証済みモデルを作成するために使用できるオプションは、'CVPartition'、'Holdout'、'KFold' のいずれかのみです。

例: 'KFold',8

データ型: single | double

SGD と ASGD の収束制御

BatchLimit — バッチの最大回数

正の整数

バッチを処理する最大回数。'BatchLimit' と正の整数から構成されるコンマ区切りのペアとして指定します。BatchLimit 回のバッチが処理されると、最適化が終了します。

• 既定の設定では、次のようになります。

  • データを通す回数は PassLimit 回です。

  • 複数のソルバーを指定し、SGD または ASGD を使用して次のソルバーの初期近似値を取得する場合、既定値は ceil(1e6/BatchSize) です。BatchSize は名前と値のペアの引数 'BatchSize' の値です。

• BatchLimit を指定した場合、fitrlinear では、BatchLimit と PassLimit の引数のうち、処理する観測値の数が少なくなる方が使用されます。

例: 'BatchLimit',100

データ型: single | double

BetaTolerance — 線形係数およびバイアス項の相対許容誤差

1e-4 (既定値) | 非負のスカラー

線形係数およびバイアス項 (切片) の相対許容誤差。'BetaTolerance' と非負のスカラーから構成されるコンマ区切りのペアとして指定します。

$$B_t=\left[{\beta }_t{}^{\prime }{b}_t\right]$$ であるとします。これは、最適化反復 t における係数およびバイアス項のベクトルです。$${\Vert \frac{B_t-B_{t-1}}{B_t}\Vert }_2<\text{BetaTolerance}$$ で最適化が終了します。

Solver で指定された最後のソルバーで収束する場合、最適化が終了します。それ以外の場合、Solver で指定された次のソルバーが使用されます。

例: 'BetaTolerance',1e-6

データ型: single | double

NumCheckConvergence — 次回の収束チェックの前にバッチを処理する回数

正の整数

次回の収束チェックの前にバッチを処理する回数。'NumCheckConvergence' と正の整数から構成されるコンマ区切りのペアとして指定します。

バッチのサイズの指定について、BatchSize を参照してください。

既定の設定では、データセット全体が通されるたびに約 10 回収束がチェックされます。

例: 'NumCheckConvergence',100

データ型: single | double

PassLimit — 最大通過回数

1 (既定値) | 正の整数

データを通す最大回数。'PassLimit' と正の整数から構成されるコンマ区切りのペアとして指定します。

データが完全に 1 回通されると、すべての観測値が fitrlinear で処理されます。

データが通される回数が PassLimit になると、fitrlinear は最適化を終了します。

BatchLimit を指定した場合、fitrlinear では、BatchLimit と PassLimit の引数のうち、処理する観測値の数が少なくなる方が使用されます。詳細は、アルゴリズムを参照してください。

例: 'PassLimit',5

データ型: single | double

ValidationData — 最適化の収束を検出するための検証データ

cell 配列 | テーブル

最適化の収束を検出するための検証データ。'ValidationData' と cell 配列またはテーブルで構成されるコンマ区切りのペアとして指定します。

最適化時に、ValidationData の損失が定期的に推定されます。検証データの損失が増加する場合、最適化が終了します。詳細は、アルゴリズムを参照してください。交差検証を使用してハイパーパラメーターを最適化する方法については、CrossVal など交差検証のオプションを参照してください。

応答変数を含む予測子データの table Tbl を使用する場合、ValidationData を table として指定できます。この場合、ValidationData は、Tbl 内に含まれるものと同じ予測子および応答を格納していなければなりません。ソフトウェアは、Tbl が重さのベクトルを含む場合であっても、観測値に重みを適用することはありません。重みを指定するには、ValidationData を cell 配列として指定しなければなりません。

ValidationData を cell 配列として指定する場合、次の形式でなければなりません。

• ValidationData{1} は、予測子データと同じデータ型および方向でなければなりません。つまり、予測子行列 X を使用する場合、ValidationData{1} は、予測子データが X と同じ方向で格納されている m 行 p 列または p 行 m 列の非スパース行列またはスパース行列でなければなりません。学習データ X の予測子変数と ValidationData{1} の予測子変数は対応していなければなりません。同様に、予測子データの予測子 table Tbl を使用する場合、ValidationData{1} は、Tbl に含まれるものと同じ予測子変数を格納していなければなりません。ValidationData{1} と予測子データの観測値の数が同じである必要はありません。

• ValidationData{2} は応答変数 (Y または ResponseVarName) のデータ型および形式と一致しなければなりません。ValidationData{2} が応答の配列である場合、その要素数は ValidationData{1} にある観測値の数と同じでなければなりません。ValidationData{1} が table である場合、ValidationData{2} はその table 内の応答変数の名前とすることができます。同じ ResponseVarName または formula を使用する場合、ValidationData{2} を [] として指定できます。

• 必要に応じて、ValidationData{3} を観測値の重みについての m 次元の数値ベクトル、または観測値の重みを含むテーブル ValidationData{1} 内の変数名として指定できます。検証データに関する重みは、合計が 1 になるように正規化されます。

ValidationData を指定し、コマンド ラインで検証損失を表示するには、0 より大きい値を Verbose に指定します。

Solver で指定された最後のソルバーで収束する場合、最適化が終了します。それ以外の場合、Solver で指定された次のソルバーが使用されます。

既定の設定では、検証データの損失を監視することによる収束の検出は行われません。

GradientTolerance — 勾配の絶対許容誤差

1e-6 (既定値) | 非負のスカラー

勾配の絶対許容誤差。'GradientTolerance' と非負のスカラーから構成されるコンマ区切りのペアとして指定します。GradientTolerance は、Solver の値が 'bfgs'、'lbfgs' または 'sparsa' である場合に適用されます。

最適化反復 t における係数およびバイアス項に関する目的関数の勾配ベクトルを $$\nabla {ℒ}_t$$ とします。$${\Vert \nabla {ℒ}_t\Vert }_{\infty }=\max \left|\nabla {ℒ}_t\right|<\text{GradientTolerance}$$ で最適化が終了します。

BetaTolerance も指定した場合、いずれかの終了条件が fitrlinear で満たされると最適化が終了します。

Solver で指定された最後のソルバーで fitrlinear が収束する場合、最適化が終了します。それ以外の場合、fitrlinear は Solver で指定された次のソルバーを使用します。

例: 'GradientTolerance',eps

データ型: single | double

IterationLimit — 最適化反復の最大回数

1000 (既定値) | 正の整数

最適化反復の最大回数。'IterationLimit' と正の整数から構成されるコンマ区切りのペアとして指定します。IterationLimit は、Solver の値が 'bfgs'、'lbfgs' または 'sparsa' である場合に適用されます。

例: 'IterationLimit',1e7

データ型: single | double

双対 SGD 最適化の収束制御

BetaTolerance — 線形係数およびバイアス項の相対許容誤差

1e-4 (既定値) | 非負のスカラー

線形係数およびバイアス項 (切片) の相対許容誤差。'BetaTolerance' と非負のスカラーから構成されるコンマ区切りのペアとして指定します。

$$B_t=\left[{\beta }_t{}^{\prime }{b}_t\right]$$ であるとします。これは、最適化反復 t における係数およびバイアス項のベクトルです。$${\Vert \frac{B_t-B_{t-1}}{B_t}\Vert }_2<\text{BetaTolerance}$$ で最適化が終了します。

DeltaGradientTolerance も指定した場合、いずれかの終了条件が満たされると最適化が終了します。

Solver で指定された最後のソルバーで収束する場合、最適化が終了します。それ以外の場合、Solver で指定された次のソルバーが使用されます。

例: 'BetaTolerance',1e-6

データ型: single | double

DeltaGradientTolerance — 勾配差分の許容誤差

0.1 (既定値) | 非負のスカラー

上位および下位プールのカルーシュ・キューン・タッカー (KKT) 相補性条件違反値の間における勾配差分の許容誤差。'DeltaGradientTolerance' と非負のスカラーから構成されるコンマ区切りのペアとして指定します。DeltaGradientTolerance は、Solver の値が 'dual' である場合のみ適用されます。

• KKT 違反値の大きさが DeltaGradientTolerance より小さい場合、fitrlinear は最適化を終了させます。

• Solver で指定された最後のソルバーで fitrlinear が収束する場合、最適化が終了します。それ以外の場合、fitrlinear は Solver で指定された次のソルバーを使用します。

例: 'DeltaGapTolerance',1e-2

データ型: double | single

NumCheckConvergence — 次回の収束チェックの前に処理するデータセット全体が通される回数

5 (既定値) | 正の整数

次回の収束チェックの前に処理するデータセット全体が通される回数。'NumCheckConvergence' と正の整数から構成されるコンマ区切りのペアとして指定します。

例: 'NumCheckConvergence',100

データ型: single | double

PassLimit — 最大通過回数

10 (既定値) | 正の整数

データを通す最大回数。'PassLimit' と正の整数から構成されるコンマ区切りのペアとして指定します。

データが完全に 1 回通されると、すべての観測値が処理されます。

データが通される回数が PassLimit になると、最適化が終了します。

例: 'PassLimit',5

データ型: single | double

ValidationData — 最適化の収束を検出するための検証データ

cell 配列 | テーブル

最適化の収束を検出するための検証データ。'ValidationData' と cell 配列またはテーブルで構成されるコンマ区切りのペアとして指定します。

最適化時に、ValidationData の損失が定期的に推定されます。検証データの損失が増加する場合、最適化が終了します。詳細は、アルゴリズムを参照してください。交差検証を使用してハイパーパラメーターを最適化する方法については、CrossVal など交差検証のオプションを参照してください。

応答変数を含む予測子データの table Tbl を使用する場合、ValidationData を table として指定できます。この場合、ValidationData は、Tbl 内に含まれるものと同じ予測子および応答を格納していなければなりません。ソフトウェアは、Tbl が重さのベクトルを含む場合であっても、観測値に重みを適用することはありません。重みを指定するには、ValidationData を cell 配列として指定しなければなりません。

ValidationData を cell 配列として指定する場合、次の形式でなければなりません。

• ValidationData{1} は、予測子データと同じデータ型および方向でなければなりません。つまり、予測子行列 X を使用する場合、ValidationData{1} は、予測子データが X と同じ方向で格納されている m 行 p 列または p 行 m 列の非スパース行列またはスパース行列でなければなりません。学習データ X の予測子変数と ValidationData{1} の予測子変数は対応していなければなりません。同様に、予測子データの予測子 table Tbl を使用する場合、ValidationData{1} は、Tbl に含まれるものと同じ予測子変数を格納していなければなりません。ValidationData{1} と予測子データの観測値の数が同じである必要はありません。

• ValidationData{2} は応答変数 (Y または ResponseVarName) のデータ型および形式と一致しなければなりません。ValidationData{2} が応答の配列である場合、その要素数は ValidationData{1} にある観測値の数と同じでなければなりません。ValidationData{1} が table である場合、ValidationData{2} はその table 内の応答変数の名前とすることができます。同じ ResponseVarName または formula を使用する場合、ValidationData{2} を [] として指定できます。

• 必要に応じて、ValidationData{3} を観測値の重みについての m 次元の数値ベクトル、または観測値の重みを含むテーブル ValidationData{1} 内の変数名として指定できます。検証データに関する重みは、合計が 1 になるように正規化されます。

ValidationData を指定し、コマンド ラインで検証損失を表示するには、0 より大きい値を Verbose に指定します。

Solver で指定された最後のソルバーで収束する場合、最適化が終了します。それ以外の場合、Solver で指定された次のソルバーが使用されます。

既定の設定では、検証データの損失を監視することによる収束の検出は行われません。

BFGS、LBFGS および SpaRSA の収束制御

BetaTolerance — 線形係数およびバイアス項の相対許容誤差

1e-4 (既定値) | 非負のスカラー

線形係数およびバイアス項 (切片) の相対許容誤差。非負のスカラーとして指定します。

$$B_t=\left[{\beta }_t{}^{\prime }{b}_t\right]$$ であるとします。これは、最適化反復 t における係数およびバイアス項のベクトルです。$${\Vert \frac{B_t-B_{t-1}}{B_t}\Vert }_2<\text{BetaTolerance}$$ で最適化が終了します。

GradientTolerance も指定した場合、いずれかの終了条件が満たされると最適化が終了します。

Solver で指定された最後のソルバーで収束する場合、最適化が終了します。それ以外の場合、Solver で指定された次のソルバーが使用されます。

例: 'BetaTolerance',1e-6

データ型: single | double

GradientTolerance — 勾配の絶対許容誤差

1e-6 (既定値) | 非負のスカラー

勾配の絶対許容誤差。非負のスカラーとして指定します。

最適化反復 t における係数およびバイアス項に関する目的関数の勾配ベクトルを $$\nabla {ℒ}_t$$ とします。$${\Vert \nabla {ℒ}_t\Vert }_{\infty }=\max \left|\nabla {ℒ}_t\right|<\text{GradientTolerance}$$ で最適化が終了します。

BetaTolerance も指定した場合、いずれかの終了条件が満たされると最適化が終了します。

指定された最後のソルバーで収束する場合、最適化が終了します。それ以外の場合、Solver で指定された次のソルバーが使用されます。

例: 'GradientTolerance',1e-5

データ型: single | double

HessianHistorySize — ヘッセ近似の履歴バッファーのサイズ

15 (既定値) | 正の整数

ヘッセ近似の履歴バッファーのサイズ。'HessianHistorySize' と正の整数から構成されるコンマ区切りのペアとして指定します。各反復において、最新の HessianHistorySize 回の反復の統計量を使用してヘッシアンが構成されます。

SpaRSA の場合、'HessianHistorySize' はサポートされません。

例: 'HessianHistorySize',10

データ型: single | double

IterationLimit — 最適化反復の最大回数

1000 (既定値) | 正の整数

最適化反復の最大回数。'IterationLimit' と正の整数から構成されるコンマ区切りのペアとして指定します。IterationLimit は、Solver の値が 'bfgs'、'lbfgs' または 'sparsa' である場合に適用されます。

例: 'IterationLimit',500

データ型: single | double

ValidationData — 最適化の収束を検出するための検証データ

cell 配列 | テーブル

最適化の収束を検出するための検証データ。'ValidationData' と cell 配列またはテーブルで構成されるコンマ区切りのペアとして指定します。

最適化時に、ValidationData の損失が定期的に推定されます。検証データの損失が増加する場合、最適化が終了します。詳細は、アルゴリズムを参照してください。交差検証を使用してハイパーパラメーターを最適化する方法については、CrossVal など交差検証のオプションを参照してください。

応答変数を含む予測子データの table Tbl を使用する場合、ValidationData を table として指定できます。この場合、ValidationData は、Tbl 内に含まれるものと同じ予測子および応答を格納していなければなりません。ソフトウェアは、Tbl が重さのベクトルを含む場合であっても、観測値に重みを適用することはありません。重みを指定するには、ValidationData を cell 配列として指定しなければなりません。

ValidationData を cell 配列として指定する場合、次の形式でなければなりません。

• ValidationData{1} は、予測子データと同じデータ型および方向でなければなりません。つまり、予測子行列 X を使用する場合、ValidationData{1} は、予測子データが X と同じ方向で格納されている m 行 p 列または p 行 m 列の非スパース行列またはスパース行列でなければなりません。学習データ X の予測子変数と ValidationData{1} の予測子変数は対応していなければなりません。同様に、予測子データの予測子 table Tbl を使用する場合、ValidationData{1} は、Tbl に含まれるものと同じ予測子変数を格納していなければなりません。ValidationData{1} と予測子データの観測値の数が同じである必要はありません。

• ValidationData{2} は応答変数 (Y または ResponseVarName) のデータ型および形式と一致しなければなりません。ValidationData{2} が応答の配列である場合、その要素数は ValidationData{1} にある観測値の数と同じでなければなりません。ValidationData{1} が table である場合、ValidationData{2} はその table 内の応答変数の名前とすることができます。同じ ResponseVarName または formula を使用する場合、ValidationData{2} を [] として指定できます。

• 必要に応じて、ValidationData{3} を観測値の重みについての m 次元の数値ベクトル、または観測値の重みを含むテーブル ValidationData{1} 内の変数名として指定できます。検証データに関する重みは、合計が 1 になるように正規化されます。

ValidationData を指定し、コマンド ラインで検証損失を表示するには、0 より大きい値を Verbose に指定します。

Solver で指定された最後のソルバーで収束する場合、最適化が終了します。それ以外の場合、Solver で指定された次のソルバーが使用されます。

既定の設定では、検証データの損失を監視することによる収束の検出は行われません。

ハイパーパラメーターの最適化

OptimizeHyperparameters — 最適化するパラメーター

'none' (既定値) | 'auto' | 'all' | 使用可能パラメーター名の string 配列または cell 配列 | optimizableVariable オブジェクトのベクトル

最適化するパラメーター。'OptimizeHyperparameters' と次のいずれかから構成されるコンマ区切りのペアとして指定します。

• 'none' — 最適化を行いません。

• 'auto' — {'Lambda','Learner'} を使用します。

• 'all' — すべての使用可能パラメーターを最適化します。

• 使用可能パラメーター名の string 配列または cell 配列。

• optimizableVariable オブジェクトのベクトル。通常は hyperparameters の出力です。

最適化では、パラメーターを変化させることにより、fitrlinear の交差検証損失 (誤差) を最小化しようとします。交差検証のタイプおよびその他の最適化の側面を制御するには、名前と値のペア HyperparameterOptimizationOptions を使用します。

メモ

'OptimizeHyperparameters' の値は、他の名前と値の引数を使用して指定した値より優先されます。たとえば、'OptimizeHyperparameters' を 'auto' に設定すると、fitrlinear は 'auto' オプションに対応するハイパーパラメーターを最適化して、ハイパーパラメーターに指定された値を無視します。

fitrlinear では、以下のパラメーターを使用できます。

• Lambda — fitrlinear は、既定では範囲 [1e-5/NumObservations,1e5/NumObservations] の対数スケールで、正の値を探索します。

• Learner — fitrlinear は、'svm' と 'leastsquares' で探索します。

• Regularization — fitrlinear は、'ridge' と 'lasso' で探索します。

  • Regularization が 'ridge' の場合、Solver の値は既定では 'lbfgs' に設定されます。

  • Regularization が 'lasso' の場合、Solver の値は既定では 'sparsa' に設定されます。

既定以外のパラメーターを設定するには、既定以外の値が含まれている optimizableVariable オブジェクトのベクトルを渡します。たとえば、以下のようにします。

load carsmall
params = hyperparameters('fitrlinear',[Horsepower,Weight],MPG);
params(1).Range = [1e-3,2e4];

OptimizeHyperparameters の値として params を渡します。

既定では、コマンド ラインに反復表示が表示され、最適化のハイパーパラメーターの個数に従ってプロットが表示されます。最適化とプロットにおける目的関数は、log(1 + cross-validation loss) です。反復表示を制御するには、名前と値の引数 'HyperparameterOptimizationOptions' の Verbose フィールドを設定します。プロットを制御するには、名前と値の引数 'HyperparameterOptimizationOptions' の ShowPlots フィールドを設定します。

たとえば、線形回帰の最適化を参照してください。

例: 'OptimizeHyperparameters','auto'

HyperparameterOptimizationOptions — 最適化のオプション

構造体

最適化のオプション。構造体として指定します。この引数を指定すると、名前と値の引数 OptimizeHyperparameters の効果が変化します。この構造体のフィールドは、すべてオプションです。

フィールド名	値	既定の設定
Optimizer	'bayesopt' — ベイズ最適化を使用。内部的には bayesopt が呼び出されます。 'gridsearch' — 次元ごとに NumGridDivisions の値があるグリッド探索を使用。 'randomsearch' — MaxObjectiveEvaluations 個の点で無作為に探索。 'gridsearch' では、グリッドからの一様な非復元抽出により、無作為な順序で探索します。最適化後、sortrows(Mdl.HyperparameterOptimizationResults) コマンドを使用してグリッド順のテーブルを取得できます。	'bayesopt'
AcquisitionFunctionName	'expected-improvement-per-second-plus' 'expected-improvement' 'expected-improvement-plus' 'expected-improvement-per-second' 'lower-confidence-bound' 'probability-of-improvement' オブジェクト関数のランタイムによって最適化が異なるので、名前に per-second が含まれている獲得関数は、再現性がある結果を生成しません。名前に plus が含まれている獲得関数は、領域を過剰利用している場合に動作を変更します。詳細は、獲得関数のタイプを参照してください。	'expected-improvement-per-second-plus'
MaxObjectiveEvaluations	目的関数評価の最大数。	'bayesopt' および 'randomsearch' の場合は 30、'gridsearch' の場合はグリッド全体
MaxTime	制限時間。正の実数スカラーを指定します。制限時間の単位は、tic と toc によって測定される秒です。MaxTime は関数評価を中断させないため、実行時間が MaxTime を超える可能性があります。	Inf
NumGridDivisions	'gridsearch' における各次元の値の個数。値は、各次元の値の個数を表す正の整数のベクトル、またはすべての次元に適用されるスカラーが可能です。カテゴリカル変数の場合、このフィールドは無視されます。	10
ShowPlots	プロットを表示するかどうかを示す論理値。true の場合、最良の観測された目的関数の値が反復回数に対してプロットされます。ベイズ最適化を使用する場合 (Optimizer が 'bayesopt')、最良の推定された目的関数値もプロットされます。最良の観測された目的関数値および最良の推定された目的関数値は、反復表示の BestSoFar (observed) 列および BestSoFar (estim.) 列の値にそれぞれ対応しています。これらの値は、Mdl.HyperparameterOptimizationResults のプロパティ ObjectiveMinimumTrace および EstimatedObjectiveMinimumTrace で確認できます。問題にベイズ最適化の最適化パラメーターが 1 つまたは 2 つある場合、ShowPlots はパラメーターに対する目的関数のモデルもプロットします。	true
SaveIntermediateResults	Optimizer が 'bayesopt' である場合に結果を保存するかどうかを示す論理値。true の場合、'BayesoptResults' という名前のワークスペース変数が反復ごとに上書きされます。この変数は BayesianOptimization オブジェクトです。	false
Verbose	コマンド ラインに次を表示します。 0 — 反復表示なし 1 — 反復表示あり 2 — 追加情報付きで反復表示あり 詳細については、bayesopt の名前と値の引数 Verbose およびベイズ最適化の使用による分類器の当てはめの最適化の例を参照してください。	1
UseParallel	ベイズ最適化を並列実行するかどうかを示す論理値。並列実行には Parallel Computing Toolbox™ が必要です。並列でのタイミングに再現性がないため、並列ベイズ最適化で再現性のある結果が生成されるとは限りません。詳細については、並列ベイズ最適化を参照してください。	false
Repartition	反復ごとに交差検証を再分割するかどうかを示す論理値。false の場合、オプティマイザーは単一の分割を最適化に使用します。 分割ノイズが考慮されるので、通常は true に設定すると最も確実な結果が得られます。ただし、true で良好な結果を得るには、2 倍以上の関数評価が必要になります。	false
以下の 3 つのオプションは 1 つだけ使用できます。
CVPartition	cvpartition によって作成される cvpartition オブジェクト	交差検証フィールドが指定されていない場合 'Kfold',5
Holdout	ホールドアウトの比率を表す範囲 (0,1) のスカラー
Kfold	1 より大きい整数

例: 'HyperparameterOptimizationOptions',struct('MaxObjectiveEvaluations',60)

データ型: struct

出力引数

Mdl — 学習済みの線形回帰モデル

RegressionLinear モデル オブジェクト | RegressionPartitionedLinear 交差検証済みモデル オブジェクト

学習済みの線形回帰モデル。RegressionLinear モデル オブジェクトまたは RegressionPartitionedLinear 交差検証済みモデル オブジェクトとして返されます。

名前と値のペアの引数 KFold、Holdout、CrossVal、CVPartition のいずれかを設定した場合、Mdl は RegressionPartitionedLinear 交差検証済みモデル オブジェクトになります。それ以外の場合、Mdl は RegressionLinear モデル オブジェクトになります。

Mdl のプロパティを参照するには、ドット表記を使用します。たとえば、推定された係数のベクトルまたは行列を表示するには、コマンド ウィンドウに Mdl.Beta と入力します。

メモ

他の回帰モデルとは異なり、また、メモリ消費を節約するため、学習データや最適化の詳細 (収束履歴など) は RegressionLinear および RegressionPartitionedLinear モデル オブジェクトに格納されません。

FitInfo — 最適化の詳細

構造体配列

最適化の詳細。構造体配列として返されます。

各フィールドには、最終的な値または名前と値のペアの引数の指定が格納されます。たとえば、Objective は最適化が終了したときの目的関数の値です。多次元フィールドの行は Lambda の値に、列は Solver の値に対応します。

次の表で、主なフィールドを説明します。

フィールド	説明
TerminationStatus	最適化の終了理由 TerminationCode の値に対応
FitTime	秒単位の経過実時間
History	各反復における最適化情報の構造体配列。Solver フィールドには、整数符号化を使用してソルバーのタイプが格納されます。 整数 ソルバー 1 SGD 2 ASGD 3 SVM 用の双対 SGD 4 LBFGS 5 BFGS 6 SpaRSA

フィールドにアクセスするには、ドット表記を使用します。たとえば、各反復における目的関数値のベクトルにアクセスするには、FitInfo.History.Objective と入力します。

FitInfo を確認して、収束が満足できるものであるかどうかを評価することをお勧めします。

HyperparameterOptimizationResults — ハイパーパラメーターの交差検証最適化

BayesianOptimization オブジェクト | ハイパーパラメーターおよび関連する値のテーブル

ハイパーパラメーターの交差検証最適化。ハイパーパラメーターおよび関連する値が含まれている table または BayesianOptimization オブジェクトとして返されます。'OptimizeHyperparameters' の値が 'none' ではない場合、出力は空以外です。出力値は、名前と値のペアの引数 'HyperparameterOptimizationOptions' の Optimizer フィールドの値に依存します。

Optimizer フィールドの値	HyperparameterOptimizationResults の値
'bayesopt' (既定の設定)	BayesianOptimization クラスのオブジェクト
'gridsearch' または 'randomsearch'	使用したハイパーパラメーター、観測された目的関数の値 (交差検証損失)、および最低 (最良) から最高 (最悪) までの観測値の順位が格納されているテーブル

メモ

Learner が 'leastsquares' の場合、目的関数の損失項は MSE の半分になります。既定の設定では、loss は MSE を返します。したがって、loss を使用して再代入誤差または学習誤差をチェックした場合、loss によって返される MSE は、FitInfo の最適化結果や、Verbose を使用して正の詳細レベルを設定した場合にコマンド ラインに返される結果と異なります。

詳細

ウォーム スタート

"ウォーム スタート" は、収束時間を短縮するために最適化ルーチンに与えられるベータ係数およびバイアス項の初期推定値です。

低次元データの代替方法

fitclinear および fitrlinear は、高次元の線形モデルについては比較的高速に目的関数を最小化しますが、精度が犠牲になり、モデルがパラメーターに関して線形でなければならないという制限があります。予測子データ セットが低～中次元の場合は、別の分類または回帰近似関数を使用できます。次の表は、どの近似関数がデータ セットに適しているかを判断するために役立ちます。

近似させるモデル	関数	主なアルゴリズムの違い
SVM	バイナリ分類: fitcsvm マルチクラス分類: fitcecoc 回帰: fitrsvm	非線形カーネル変換に適している、予測子変数のグラム行列を計算します。 quadprog (Optimization Toolbox) を使用して二次計画法で SMO、ISDA または L1 最小化により双対問題を解きます。
線形回帰	正則化を行わない最小二乗: fitlm LASSO ペナルティを使用する正則化最小二乗: lasso リッジ回帰: ridge または lasso	lasso は、循環的な座標降下を実装します。
ロジスティック回帰	正則化を行わないロジスティック回帰: fitglm LASSO ペナルティを使用する正則化ロジスティック回帰: lassoglm	fitglm は、反復的に再重み付けした最小二乗を実装します。 lassoglm は、循環的な座標降下を実装します。

ヒント

• 観測値が列に対応するように予測子行列を配置して 'ObservationsIn','columns' を指定することをお勧めします。このようにすると、最適化実行時間が大幅に短縮される可能性があります。

• 予測子データに含まれている観測値の数が少なく、予測子変数の数が多い場合、次のようにします。

  • 'PostFitBias',true を指定します。

  • ソルバーが SGD または ASGD の場合、PassLimit を 1 より大きい正の整数 (5 や 10 など) に設定します。このように設定すると、多くの場合に精度が向上します。

• ソルバーが SGD または ASGD の場合、BatchSize は収束速度に影響を与えます。

  • BatchSize が小さすぎる場合、fitrlinear が最小値を計算するための反復回数は多くなりますが、反復ごとの勾配の計算時間は短くなります。

  • BatchSize が大きすぎる場合、fitrlinear が最小値を計算するための反復回数は少なくなりますが、反復ごとの勾配の計算時間は長くなります。

• 学習率 (LearnRate を参照) が大きいと、最小値への収束が高速になりますが、発散 (最小値の限度を超える状態) の可能性があります。学習率が小さいと最小値への収束が保証されますが、終了までに時間がかかる可能性があります。

• LASSO ペナルティを使用する場合は、さまざまな値の TruncationPeriod を試してください。たとえば、TruncationPeriod を 1、10 に設定してから 100 に設定します。

• 効率のため、fitrlinear は予測子データを標準化しません。X を標準化するには、次のように入力します。

  X = bsxfun(@rdivide,bsxfun(@minus,X,mean(X,2)),std(X,0,2));

  このコードでは、予測子が行、観測値が列に対応するように X が配置されている必要があります。また、メモリを節約するため、このコードは元の予測子データを標準化されたデータに置き換えます。

• モデルに学習をさせた後で、新しいデータについて応答を予測する C/C++ コードを生成できます。C/C++ コードの生成には MATLAB Coder™ が必要です。詳細については、コード生成の紹介を参照してください。

アルゴリズム

• ValidationData を指定した場合、目的関数の最適化時に以下が行われます。

  • fitrlinear は、現在のモデルを使用して ValidationData の検証損失を定期的に推定し、最小の推定値を追跡します。

  • fitrlinear は、検証損失を推定するときに、推定値を最小の推定値と比較します。

  • 以後の検証損失の推定値が最小推定値の 5 倍より大きくなった場合、fitrlinear は最適化を終了します。

• ValidationData を指定して交差検証ルーチン (CrossVal、CVPartition、Holdout または KFold) を実装した場合、次のようになります。

  1. fitrlinear は、選択された交差検証ルーチンに従って X と Y (または Tbl) を無作為に分割します。

  2. fitrlinear は、学習データの分割を使用してモデルに学習をさせます。目的関数の最適化時に、fitrlinear は最適化を終了させるための他の可能な方法として ValidationData を使用します (詳細については、前の項目を参照)。

  3. 終了条件が満たされると、fitrlinear は最適化された線形係数および切片に基づいて学習済みのモデルを構築します。

     1. k 分割交差検証を実装した場合、fitrlinear が網羅していない学習セット分割があると、fitrlinear はステップ 2 に戻り、次の学習セット分割を使用して学習を行います。

     2. それ以外の場合、fitrlinear は学習を終了させ、交差検証済みのモデルを返します。

  4. 交差検証済みモデルの品質を判断できます。以下に例を示します。

     • ステップ 1 のホールドアウトまたは分割外データを使用して検証損失を決定するには、交差検証済みのモデルを kfoldLoss に渡します。

     • ステップ 1 のホールドアウトまたは分割外データで観測値を予測するには、交差検証済みのモデルを kfoldPredict に渡します。

参照

[1] Ho, C. H. and C. J. Lin. “Large-Scale Linear Support Vector Regression.” Journal of Machine Learning Research, Vol. 13, 2012, pp. 3323–3348.

[2] Hsieh, C. J., K. W. Chang, C. J. Lin, S. S. Keerthi, and S. Sundararajan. “A Dual Coordinate Descent Method for Large-Scale Linear SVM.” Proceedings of the 25th International Conference on Machine Learning, ICML ’08, 2001, pp. 408–415.

[3] Langford, J., L. Li, and T. Zhang. “Sparse Online Learning Via Truncated Gradient.” J. Mach. Learn. Res., Vol. 10, 2009, pp. 777–801.

[4] Nocedal, J. and S. J. Wright. Numerical Optimization, 2nd ed., New York: Springer, 2006.

[5] Shalev-Shwartz, S., Y. Singer, and N. Srebro. “Pegasos: Primal Estimated Sub-Gradient Solver for SVM.” Proceedings of the 24th International Conference on Machine Learning, ICML ’07, 2007, pp. 807–814.

[6] Wright, S. J., R. D. Nowak, and M. A. T. Figueiredo. “Sparse Reconstruction by Separable Approximation.” Trans. Sig. Proc., Vol. 57, No 7, 2009, pp. 2479–2493.

[7] Xiao, Lin. “Dual Averaging Methods for Regularized Stochastic Learning and Online Optimization.” J. Mach. Learn. Res., Vol. 11, 2010, pp. 2543–2596.

[8] Xu, Wei. “Towards Optimal One Pass Large Scale Learning with Averaged Stochastic Gradient Descent.” CoRR, abs/1107.2490, 2011.

拡張機能

tall 配列

メモリの許容量を超えるような多数の行を含む配列を計算します。

使用上の注意事項および制限事項:

• fitrlinear は tall table データをサポートしていません。

• 一部の名前と値のペアの引数は、インメモリの関数 fitrlinear と既定値および値が異なります。サポートされる名前と値のペアの引数および違いは次のとおりです。

  • 'Epsilon'

  • 'ObservationsIn' — 'rows' のみをサポートします。

  • 'Lambda' — 'auto' (既定値) またはスカラーを指定できます。

  • 'Learner'

  • 'Regularization' — 'ridge' のみをサポートします。

  • 'Solver' — 'lbfgs' のみをサポートします。

  • 'Verbose' — 既定値は 1

  • 'Beta'

  • 'Bias'

  • 'FitBias' — true のみをサポートします。

  • 'Weights' — 値は tall 配列でなければなりません。

  • 'HessianHistorySize'

  • 'BetaTolerance' — 既定値は 1e-3 に緩和されます。

  • 'GradientTolerance' — 既定値は 1e-3 に緩和されます。

  • 'IterationLimit' — 既定値は 20 に緩和されます。

  • 'OptimizeHyperparameters' — 'Regularization' パラメーターの値は 'ridge' でなければなりません。

  • 'HyperparameterOptimizationOptions' — 交差検証として、tall 最適化では 'Holdout' 検証のみがサポートされます。既定では、データの 20% がホールドアウト検証データとして選択されて確保され、残りのデータがモデルの学習に使用されます。この引数を使用してホールドアウトの比率に別の値を指定できます。たとえば、データの 30% を検証データとして確保するには 'HyperparameterOptimizationOptions',struct('Holdout',0.3) と指定します。

• tall 配列の場合、fitrlinear は各反復で損失と勾配の計算を tall 配列のさまざまな部分に分散させることにより LBFGS を実装します。他のソルバーでは tall 配列を使用できません。

  Beta と Bias の初期値が与えられなかった場合、fitrlinear はデータの一部に対して局所的にモデルを当てはめ、平均化で係数を結合することにより、はじめにパラメーターの初期推定値を改善します。

詳細は、tall 配列を参照してください。

自動並列サポート

Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

ハイパーパラメーターの最適化を並列実行するには、関数 fitrlinear を呼び出すときに名前と値の引数 'HyperparameterOptimizationOptions', struct('UseParallel',true) を指定します。

並列的なハイパーパラメーターの最適化の詳細については、並列ベイズ最適化を参照してください。

並列計算の全般的な情報については、自動並列サポートを使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2016a で導入

R2022a: ハイパーパラメーターの最適化で使用されるソルバーを正則化手法に基づいて決定

R2022a 以降では、ハイパーパラメーターを最適化するように指定した場合に、Solver の値を指定しないと、最適化プロセスの各反復で選択された正則化タイプに応じて、記憶制限 BFGS (LBFGS) ソルバーまたは可分近似によるスパース再構成 (SpaRSA) ソルバーのいずれかが fitrlinear で使用されます。

• Regularization が 'ridge' の場合、Solver の値は既定では 'lbfgs' に設定されます。

• Regularization が 'lasso' の場合、Solver の値は既定では 'sparsa' に設定されます。

以前のリリースでは、ハイパーパラメーターの最適化での既定のソルバーの選択には、正則化タイプ、学習器タイプ、予測子の数など、さまざまな要因が関係していました。詳細については、Solver を参照してください。

参考

fitrsvm | fitlm | lasso | ridge | fitclinear | predict | kfoldPredict | kfoldLoss | RegressionLinear | RegressionPartitionedLinear

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい